IR - 08 - Evaluation
Data:
Sito corso: link
Slides:
In questa lezione abbiamo affrontato il problema di come valutare le performance di un sistema di IR.
Capire se un sistema di IR sta funzionando bene o male è un grosso problema. In particolare è fondamentale avere degli strumenti e delle tecniche che ci permettono di capire se le scelte che abbiamo effettuato durante l'implementazione dei vari componenti del sistema sono ottimali, nel senso che sono le migliori possibili.
Per poter valutare un sistema di IR, ed eventualmente confrontarlo con altri sistemi di IR, nasce la necessità di trovare un benchmark, che nel contesto dei sistemi IR viene costruito utilizzando quello che nella terminologia tecnica è chiamato gold standard.
In generale un gold standard è ottenuto effettuando i seguenti steps:
Si definiscono delle query che soddisfano determinati information needs di futuri utenti che andranno ad utilizzare il sistema.
Si applicano le query al sistema di IR che si vuole valutare per ottenere, per ogni query, i relativi documenti ritenuti rilevanti.
Un gruppo di esperti valuta, per ogni coppia \((\text{query}, \text{doc})\) ritornata dal sistema, se quel doc era effettivamente rilevante o no per quella query.
Questo procedimento è chiamato Labaled Document Collections, ed è un gold standard per la valutazione di sistemi IR.
Notiamo che l'applicazione di questo metodo di valutazione ha varie problematiche. Prima tra tutte è la presenza di un forte bias da parte di chi valuta il sistema rispetto a quello che viene ritornato dal sistema di IR. L'utente medio sarà infatti portato a pensare quasi in modo automatico che i documenti ritornati prima sono più significativi per la query effettuata, anche quando magari non è così.
In generale questo approccio richiede un intensivo lavoro umano, e dunque può essere applicato solamente a collezioni di documenti di piccola o al massimo media grandezza, andando quindi a creare un problema di coverage della vera collezione di documenti.
Le metriche più semplici ed utilizzate per valutare le performance di un sistema di IR sono la precision e la recall. Definite come segue:
Precision: La precision ci serve per capire quanti dei documenti ritornati sono effettivamente utili. Più la precision è alta, e più il sistema è precisco nel fornirci solo cose utili rispetto a quello che ci serve.
\[\text{Precision} = \frac{\text{# documenti rilevanti ritornati}}{\text{# documenti ritornati}}\]
Recall: La recall invece ci dice quant'è la percentuale di documenti utili ritornati, rispetto a tutti i documenti utili. Più alta è la recall e più il sistema ci ritorna tutte le cose che potenzialmente ci potrebbero servire.
\[\text{Recall} = \frac{\text{# documenti rilevanti ritornati}}{\text{# documenti rilevanti totali}}\]
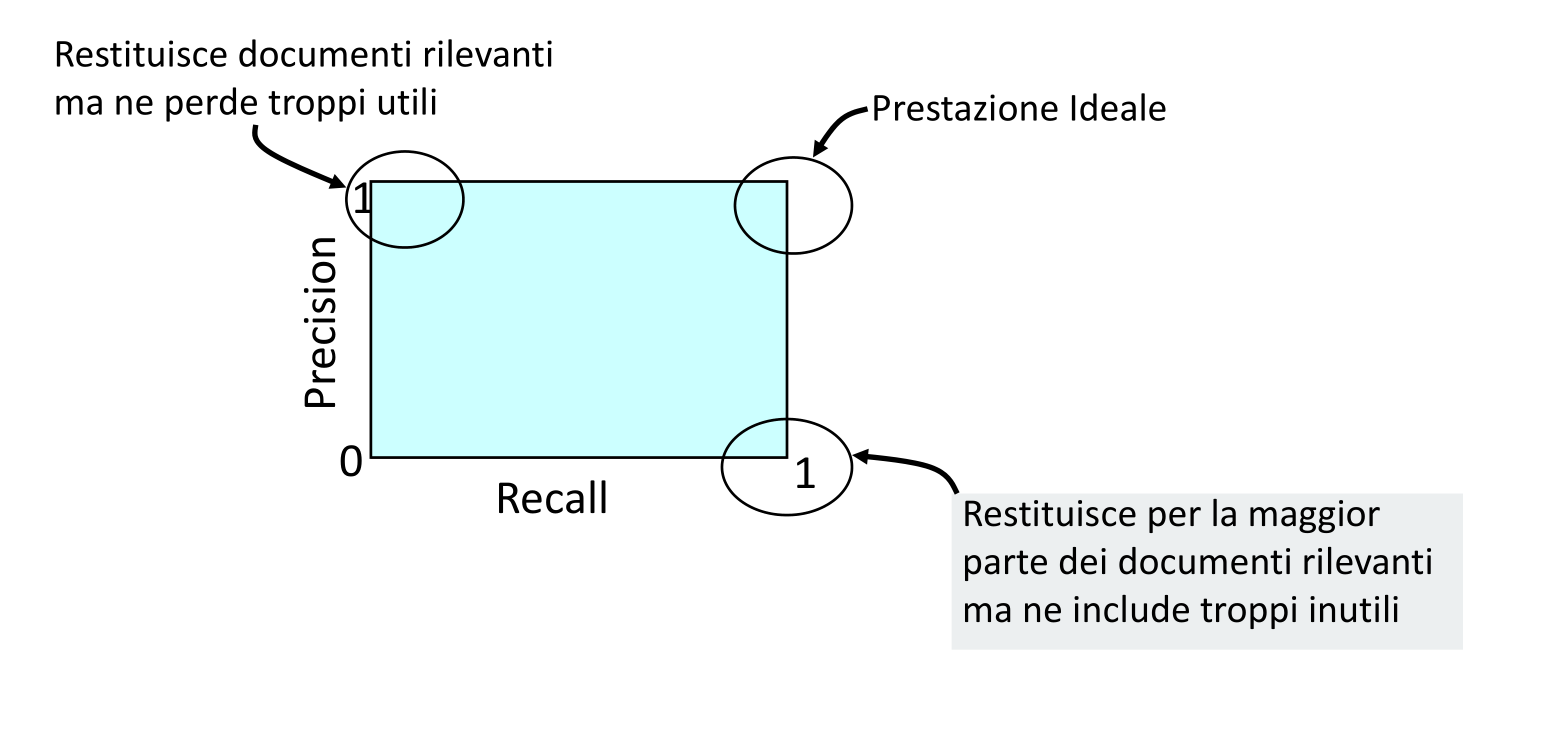
La precision e la recall sono misure in conflitto tra loro. Infatti, più alta sarà la precisione, e più bassa sarà la recall, e viceversa. Per convenzione se un sistema non risponde mai la sua precisione è \(1\).
Per calcolare queste due misure è utile formularle in termine di tenere a mente la seguente tabella di contingenza
\[\begin{array}{c | c | c} \text{} & \textbf{Retrieved} & \textbf{Not Retrieved} \\ \hline \textbf{Relevant} & \text{True Positive (tp)} & \text{False Negative (fn)} \\ \textbf{Irrelevant} & \text{False Positive (fp)} & \text{True Negative (tn)} \\ \end{array}\]
con questo formalismo abbiamo che
\[\begin{align} \text{precision} &= \frac{\text{tp}}{(\text{tp} + \text{fp})}\\ \text{recall} &= \frac{\text{tp}}{(\text{tp} + \text{fn})}\\ \end{align}\]
Per produrre un giudizio sulla performance di un sistema di IR, l'idea è quella di combinare i valori della precision e della recall tra loro. Per fare questo esistono vari approcci diversi:
Media aritmetica: Molto spesso calcolare la semplice media aritmetica non basta, in quanto offre un giudizio fin troppo ottimista.
Media armonica: La media armonica, definita come l'inverso della media degli inversi, è invece più pessimista della semplice media aritmetica, in quanto le più piccole variazioni nei valori di precision e recall possono avere un impatto significativo sul valore finale ottenuto. Nel contesto dei sistemi di IR tale metrica è chiamata F-measure, e può essere calcolata come segue
\[\text{F} = \frac{1}{\frac12 \cdot (\frac{1}{\text{R}} + \frac{1}{\text{P}})} = \frac{2 \text{R} \text{P}}{\text{R} + \text{P}}\]
In generale quindi ci sono vari modi per combinare la precision e la recall
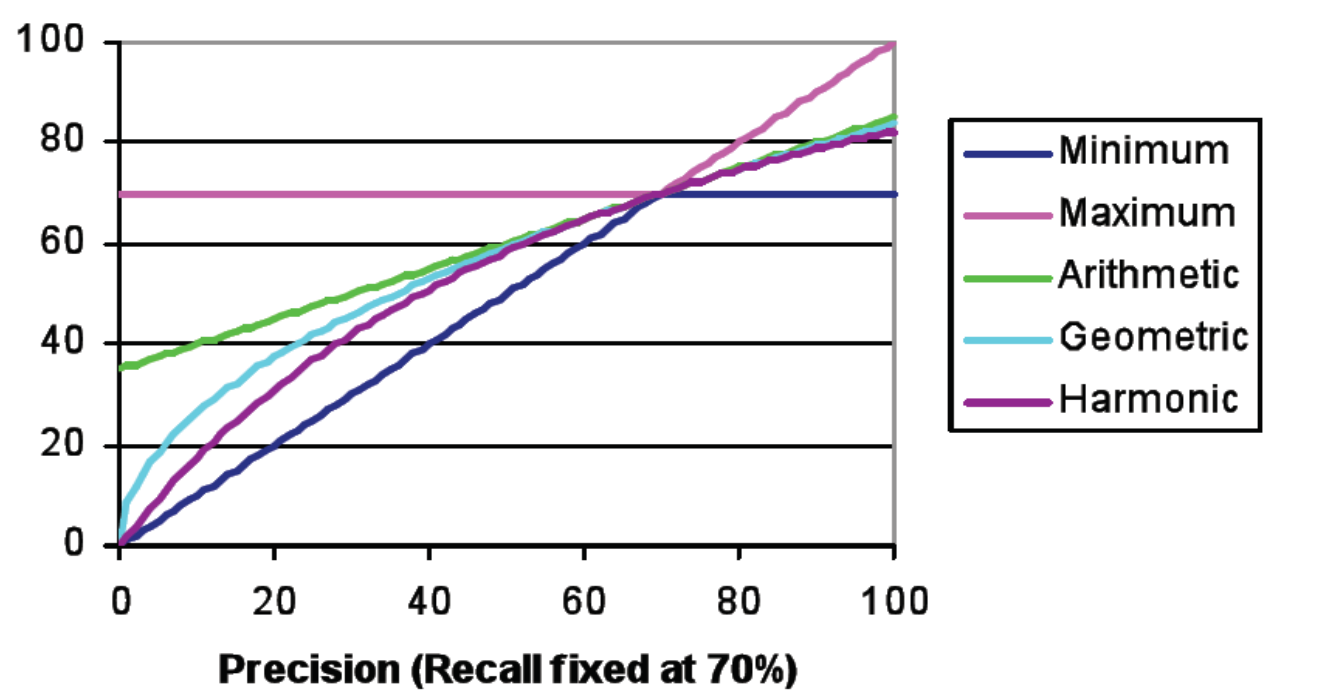
Tipicamente poi la precision e la recall vengono calcolate e combinate per ogni singola query, e poi le relative medie vengono combinate tra loro in una macro-media.
Con il crescere della dimensione delle collezioni dei documenti è diventato sempre più difficile andare a valutare un sistema di IR tramite una annotazione di ogni singolo risultato ottenuto, ovvero di ogni coppia \((\text{query}, \text{doc_ID})\). Sono state quindi definite una serie di misure che si basano sulla rilevanza dei documenti ritornata dal sistema di ranking.
Il focus si è quindi spostato dal considerare assieme la precision e la recall al considerare solamente la precision. Questa scelta è sensata in quanto per calcolare la recall dovrei sapere quanti sono tutti i documenti rilevanti per una data query, il che è molto difficile da fare per collezioni documentali molto grandi.
L'idea è quella di fissare un valore \(K\) e considerare solamente i documenti che il sistema di IR ritorna tra le prime \(K\) posizioni. La precision@K altro non è quindi che il tipico calcolo della precision ristretto però ai primi \(K\) documenti. La stessa cosa può poi essere fatta per la recall, permettendoci di calcolare la recall@K. Queste misure sono quindi definite rispetto al rank dei documenti.

Una volta che abbiamo calcolato la precision e la recall ristretta ai primi \(K\) documenti, per rendere la curva precision/recall monotona decrescente possiamo effettuare l'interpolazione, ovvero definiamo la funzione
\[P(\text{R}) = \max\big\{\text{P}' : \text{R}' \geq \text{R} \,\,\, \land \,\,\, (\text{R}', \text{S}') \in S \big\}\]
dove \(S\) è l'insieme di punti osservati (Recall, Precision).
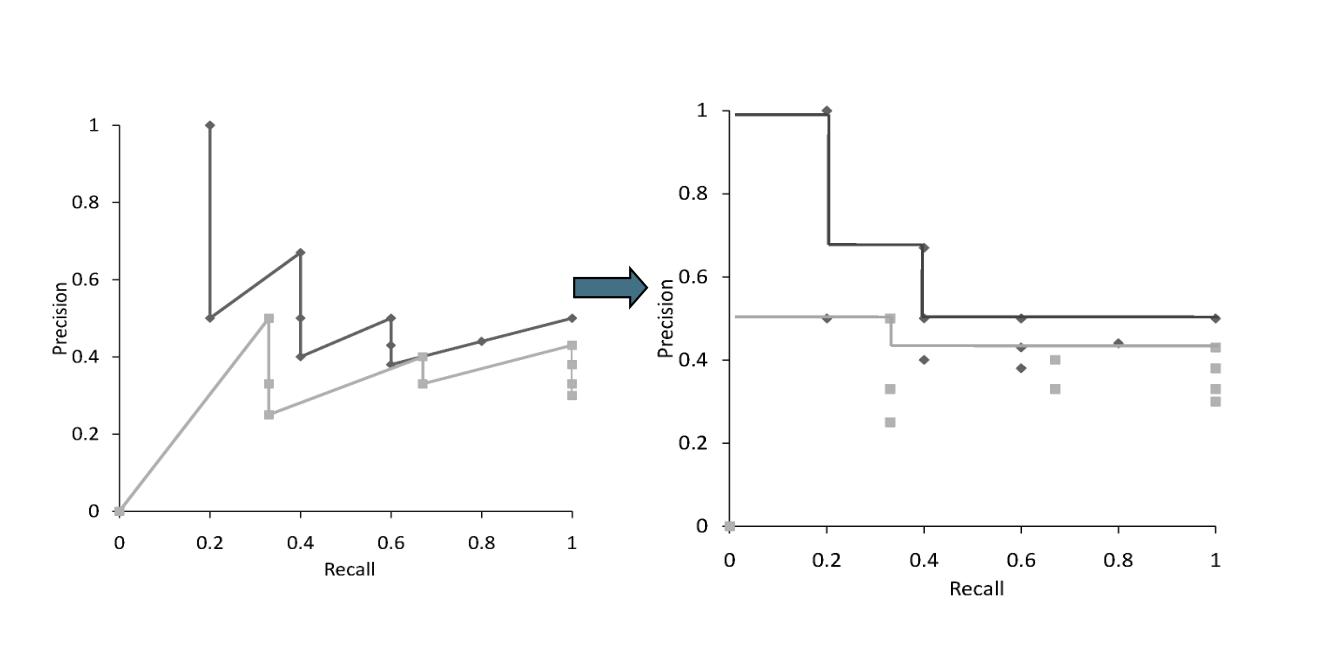
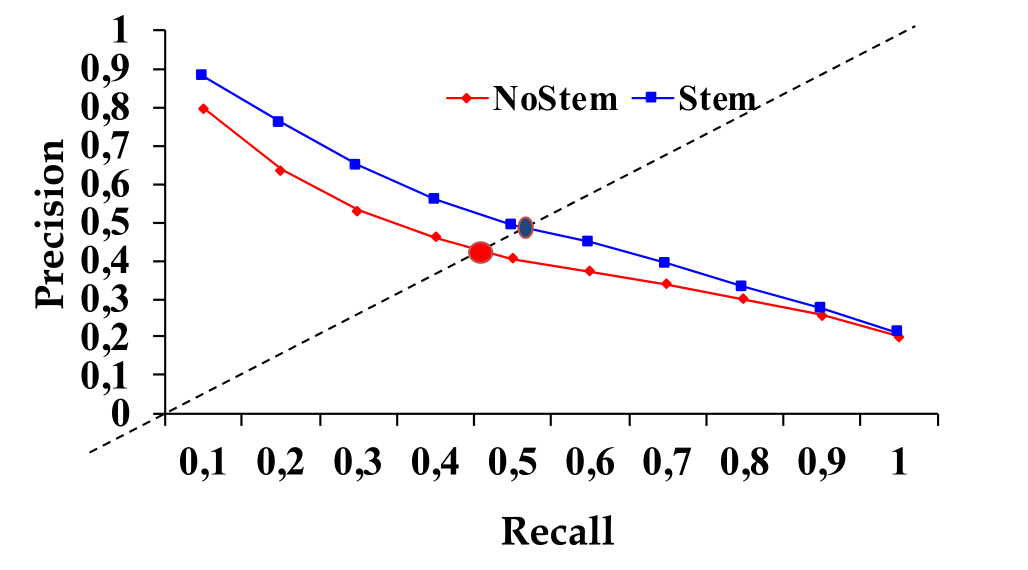
Così facendo per descrivere un sistema IR non utilizzo un numero, ma una funzione, che mappa tra loro i valori della recal e della precision. Questa funzione è chiamata curva precision/recall, e può essere applicata per comparare due sistemi IR.
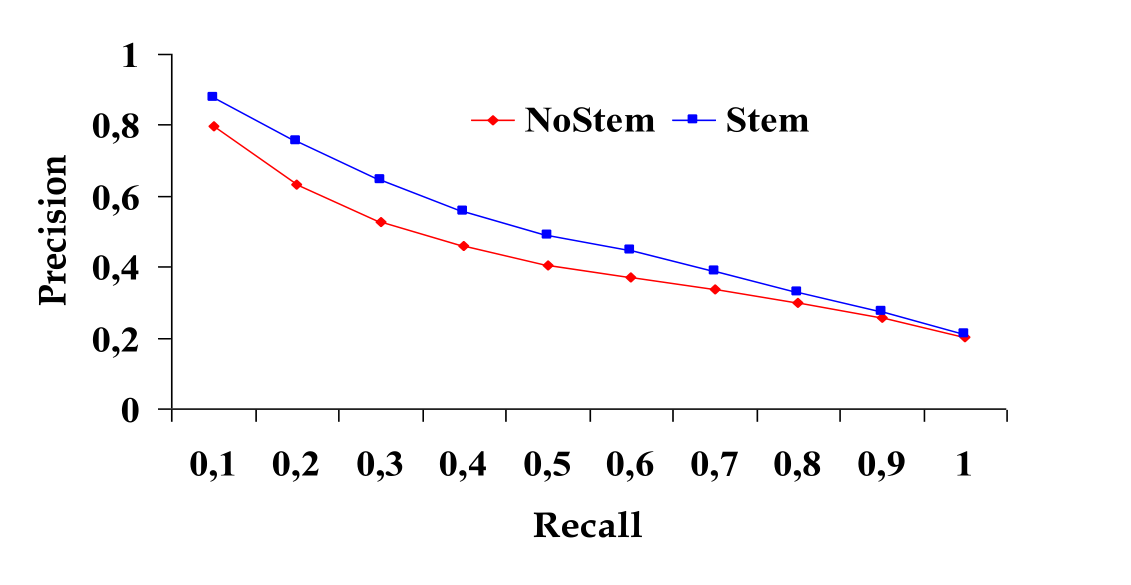
Il breakeven point è il punto della curva ottenuta tramite l'interpolazione tale che il valore della precision è uguale al valore della recall. Tale punto può essere utilizzato per "riassumere" l'andamento di un sistema.
Consideriamo le posizioni dei documenti rilevanti ritornate dall'algoritmo di ranking \(K_1, K_2, \ldots, K_r\). L'idea dietro al mean average precision (MAP) è quella di calcolare la Precision@K per ogni \(K_1, K_2, \ldots, K_r\), e poi fare la media tra questi valori.
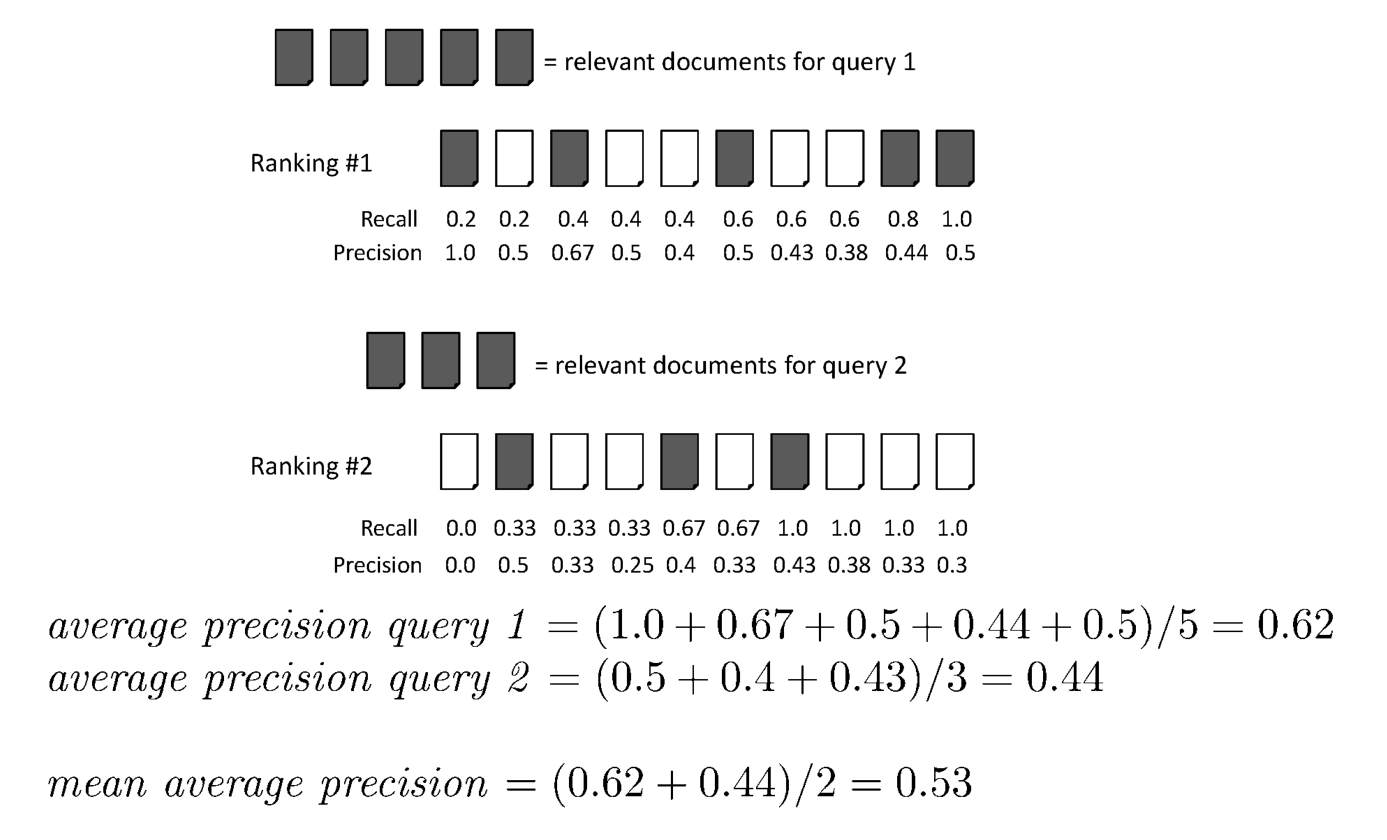
MAP assegna ad ogni query lo stesso peso, e attualmente è forse una delle metriche più utilizzate negli articoli di ricerca.
Le metriche definite fino a questo punto condividevano tutte un approccio binario alla rilavanza: o un documento era rilevante, oppure non lo era. Nella realtà però possiamo avere varie gradazioni di rilevanza, e queste ulteriori informazioni possono essere utili da prendere in considerazione al fine di misurare le performance di un sistema di IR.
Il Discounted Cumulative Gain (DCG) è una misura abbastanza famosa per misurare le performance delle search engines nel contesto del web. Essa si basa sullo sforzo che un utente mediamente pigro fa nel scegliere risultati che si trovano sempre più in baso nel ranking calcolato dalla search engine. In particolare il DCG cerca di minimizzare lo sforzo dell'utente.
Il DCG si basa sulle seguenti due assunzioni:
I documenti più rilevanti sono molto più utili dei documenti poco rilevanti rispetto all'information need dell'utente;
Più un documento è rankato in una posizione bassa, e meno è utile per l'utente, in quanto è poco probabile che l'utente lo guardi.
In questo schema quindi non abbiamo una rilevanza booleana, ma bensì graduale. In particolare la rilevanza di un documento è un numero reale che varia in \([0, r]\), con \(r > 2\).
Nel Cumulative Gain, il guadagno che ho per aver trovato per i primi \(n\) documenti con rilevanza pari a \(r_1\), \(r_2\), ..., \(r_n\), dove gli indici sono dati in base al ranking order, è uguale a
\[\text{CG} = r_1 + r_2 + ... + r_n\]
In altre parole non mi interessa la posizione del documento nel ranking fornito ma sono solo interessato dalla somma delle rilevanze dei documenti.
Nel Discounted Cumulative Gain invece diminuisco il guadagno che ogni documento mi fa fare in base alla posizione del documento all'interno del ranking. L'idea infatti è che più basso un documento rilevante si trova nel ranking finale, e meno punti mi da. La scalatura è effettuata in modo logaritmico come segue
\[\text{DCG} = r_1 + \frac{r_2}{\log 2} + \frac{r_3}{\log 3} + \ldots + \frac{r_n}{\log n}\]
Per confrontare query con un numero di documenti diversi applico la normalizzazione del DCG, che prende il nome di NDCG. In particolare normalizzo utilizzando il valore del DCG al rank \(n\) con il ranking ideale, dove il ranking ideale ritorna come primo elemento quello con più rilevenza, come secondo elemento quello con la seconda rilevanza più alta, etc.
Così facendo se il mio sistema è perfetto riceverà \(1\), e in generale ho un valore tra \([0, 1]\).
Sia
\[\text{Reciprocal Rank Score} = \frac{1}{K}\]
dove con \(K\) si indica la posizione nel ranking del primo documento rilevante ritornato. Il Mean Reciprocal Rank è la media del Reciprocal Rank su varie query.
Avere un team di esseri umani che giudichi i vari documenti per stabilire se sono rilevanti o no è una operazione molto costosa da effettuare, e può anche dare dei risultati inconsistenti, sia rispetto al tempo, che rispetto alle persone.
Tra le possibili alternative per ottenere dei benchmark da poter utilizzare troviamo il comportamenti degli utenti del sistema di IR che vogliamo valutare. Questo però può portare a varie problematiche, in quanto ad esempio è stato dimostrato da Joachmis che i documenti ritornati in posizioni più alte ricevono più user attention e più clicks. Bisogna quindi stare attenti a come si incorporano i dati ricavati dagli utenti.