IR - 09 - Ranking III
Data:
Sito corso: link
Slides:
In questa lezione abbiamo ripreso e terminato la discussione sulle funzioni di ranking.
Ricordiamo che lavorando con il modello \(\text{BIM}\) (Binary Indipendence Model), il calcolo del ranking dei documenti avviene tramite il calcolo degli odds ratios, definiti come segue
\[c_t := \log{\frac{p_t(1 - u_t)}{u_t(1 - p_t)}} = \log{\frac{p_t}{(1 - p_t)}} - \log{\frac{u_t}{(1 - u_t)}}\]
dove,
\(p_t :=\) Probabilità che il termine \(t\) compare in un documento rilevante.
\(u_t :=\) Probabilità che il termine \(t\) compare in un documento non rilevante.
Dato un documento \(d\) la sua rilevanza è quindi data da
\[\text{RSV}_d := \sum\limits_{x_t = q_t = 1} c_t\]
Quando avevamo terminato l'argomento in una lezione precedente avevamo lasciato il problema di stimare \(u_t\) e \(p_t\), per ogni termine \(t\) del vocabolario.
Un primo approccio per stimare i valori di \(u_t\) e \(p_t\) è quello di utilizzare la seguente tabella di contingenza
\[\begin{array}{c | c | c | c} & \textbf{# of relevant docs} & \textbf{# of non-relevant docs} & \textbf{total #}\\ \hline \textbf{term present} (x_t = 1) & s & \text{df}_t - s & \text{df}_t \\ \textbf{term present} (x_t = 1) & S - s & (N - \text{df}_t) - (S - s) & N - \text{df}_t \\ \textbf{total #} & S & N - S & N \\ \end{array}\]
in questo modo otteniamo le seguenti stime
\[\begin{align} p_t &= \frac{s}{S} \\ \\ u_t &= \frac{\text{df}_t - s}{N - S}\\ \end{align}\]
Notiamo però che così facendo necessitiamo comunque di conoscere i valori \(s\) e \(S\). Per fare questo esistono almeno i seguenti due approcci:
Ad-Hoc Retrieval: Consiste nel fare assunzioni molte forti al fine di semplificare il problema.
Pseudo-Relevance Feedback: Consiste nell'utilizzare l'output del sistema di IR per migliorare la stima dei documenti rilevanti.
L'Ad-Hoc retrieval si basa su effettuare due ipotesi semplificative. Queste sono:
Come prima ipotesi assumiamo che per ogni query il numero di documenti rilevanti sia una frazione molto piccola della collezione. Da questo segue che
\[u_t \approx \frac{\text{df}_t}{N}\]
e quindi
\[c_t = \log{\frac{p_t}{(1 - p_t)}} + \log{\frac{1-u_t}{u_t}} \approx \log{\frac{p_t}{1-p_t}} + \log{\frac{N}{\text{df}_t}}\]
La seconda ipotesi invece è molto più forte della prima, e consiste nell'assumere che ogni termine ha la stessa probabilità di comparire in un documento rilevante o in un documento non rilevante. Formalmente,
\[\forall \text{ termine } x_t: \,\,\,\, p_t = \frac12\]
con questa ipotesi abbiamo che
\[\log{\frac{p_t}{1 - p_t}} = 0\]
Combinando le due ipotesi descritte precedentemente otteniamo che
\[c_t \approx \log{\frac{N}{\text{df}_t}}\]
e quindi il ranking di un documento \(d\) è dato da
\[\text{RSV}_d = \sum\limits_{t: x_t=q_t=1} \log{\frac{p_t(1-u_t)}{u_t(1-p_t)}} \approx \sum\limits_{t: x_t=q_t=1} \log{\frac{N}{\text{df}_t}}\]
Questa stima può essere soddisfacente per fare il ranking di documenti brevi in caso di one-pass retrieval.
Andiamo adesso a vedere come aggiungere la term frequency e la length normalization in un setting probabilistico.
Il modello Okapi BM25 utilizza una semplificazione del modello 2-Poisson, modificata in modo empirico per aumetnare le performance. Attualmente è il metodo standard base utilizzato nei prodotti commerciali per calcolare il ranking dei documenti.
Il punto da cui iniziamo è il seguente
\[\text{RSV}_d := \sum\limits_{t \in q} \log{\frac{N}{\text{df}_t}}\]
Una prima modifica viene effettuata per introdurre la term frequency.
\[\text{RSV}_d := \sum\limits_{t \in q}\frac{(k_1 + 1)\text{tf}_{t,d}}{k_1 + \text{tf}_{t, d}} \cdot \log{\frac{N}{\text{df}_t}}\]
dove \(k_1\) è un parametro di tuning che viene utilizzato per controllare l'impatto della term frequency. Notiamo che il fattore \((k_1 + 1)\) non cambia il ranking, ma rende lo score del termine unitario (cioè che vale \(1\)), quando \(\text{tf}_{t, d} = 1\). Grazie a \(k_1\) siamo quindi in grado di limitare l'impatto che un singolo termine della query può avere sul ranking finale.
Valori tipici sono \(k_1 \in [1.2, \,\,\,2]\).
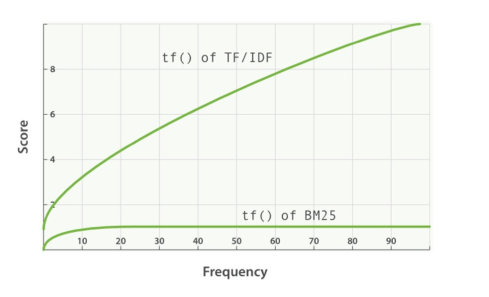
La seconda modifica viene introdotta per gestire la length normalization.
Notiamo che nei documenti più lunghi i valori della \(\text{tf}_{t, d}\) tendono naturalmente ad essere più alti. Un documento però può essere lungo per varie ragioni, tra cui:
Verbosity: Quando abbiamo tante ripetizioni degli stessi concetti. In questo caso il valore \(\text{tf}_{t, d}\) potrebbe essere troppo alto.
Larger scope: Quando si trattano vari argomenti in modo approfondito. In questo caso il valore \(\text{tf}_{t, d}\) potrebbe essere giusto.
Definiamo quindi la document length
\[L_d := \sum\limits_{t} \text{tf}_{t, d}\]
Sia poi \(L_{\text{ave}}\) la lunghezza media dei documenti della collezione. Allora il componente che andiamo ad aggiungere per introdurre la length normalization è
\[B := (1 - b) + b \cdot \frac{L_d}{L_{\text{ave}}} \,\,\,,\,\,\,\, 0\leq b \leq 1\]
dove \(b\) è un parametro di tuning che controlla l'impatto della normalizzazione nel ranking. Se \(b = 1\) abbiamo l'effetto massimo, mentre se \(b=0\) non abbiamo nessun effetto. Valori tipici per \(b\) sono \(\approx 0.75\).
La formula per il ranking diventa quindi
\[\text{RSV}_d := \sum\limits_{t \in q} \frac{(k_1 + 1) \cdot \text{tf}_{t, d}}{k_1 \cdot \Big( (1 - b) + b \cdot \frac{L_d}{L_{\text{ave}}}\Big) + \text{tf}_{t, d}} \cdot \log{\frac{N}{\text{df}_t}}\]
Tale ranking viene utilizzato nella versione più semplice di BM25.
Come ultima cosa, per gestire le query lunghe si potrebbe nuovamente verificare il problema della term frequency. La formula finale nel modello Okai BM25 è quindi la seguente
\[\text{RVS}_d := \sum\limits_{t \in q} \log{\frac{N}{\text{df}_t}} \cdot \frac{(k_1 + 1) \cdot \text{tf}_{t, d}}{k_1 \cdot \Big((1 - b) + b \cdot \frac{L_d}{L_{\text{ave}}} \Big) + \text{tf}_{t, d}} \cdot \underbrace{\frac{(k_3 + 1) \cdot \text{tf}_{t, q}}{k_3 + \text{tf}_{t, q}}}_{\text{Fattore aggiunto per le query}}\]
In totale abbiamo quindi tre parametri di tuning, che devono essere scelti in base al contesto. Tipici valori sono
\(\begin{cases} k_1, k_3 \in [1.2, \,\,\, 2] \\ b = 0.75 \end{cases}\)
I modelli di linguaggio sono un ulteriore modo per fare il ranking dei documenti tramite l'utilizzo di strumenti statistici. Un modello di linguaggio è, nella sua forma più semplice, una distribuzione di probabilità sui termini di un vocabolario.
Tramite un modello di linguaggio siamo in grado di associare ad ogni sequenza di termini (e quindi ad ogni documento), un valore di probabilità.
L'idea è quindi quella di derivare per ogni documento della collezione un modello di linguaggio. In un successivo momento poi, data una query, ci si calcola la probabilità della query rispetto ai vari modelli di linguaggio e si ordinano i documenti rispetto alle probabilità calcolate.
Troviamo quindi il seguente schema:
Definiamo il preciso modello di linguaggio che vogliamo utilizzare.
Per ogni documento, stimiamo i parametri per ottenere il relativo modello di linguaggio.
Data una query, calcoliamo la probabilità della query per ogni modello e ritorniamo i documenti più probabili.
Un modello di linguaggio può essere formalizzato come un automa a stati finiti, in cui ogni stato (nodo) rappresenta un termine, e le transazioni sono pesate da dei valori di probabilità. Detto altrimenti, un modello di linguaggio può essere formalizzato come una catena di markov. Una caratteristica importante delle catene di Markov è la dipendenza tra le varie transazioni nel tempo.
Nei modelli di linguaggio più semplici abbiamo che la probabilità di ottenere un termine non dipende dai termini visti precedentemente. Questo modello è chiamato modello unigram.
Osservazione: L'ipotesi fatta nel modello unigram è molto forte. Detto questo, più aumento la dipendenza dal contesto e più aumento le probabilità che dovrò stimare.
Nella prossima lezione andiamo a vedere come possiamo associare un modello di linguaggio ad un dato documento per poter poi effettuare il ranking.