IR - 12 - Efficient Scoring

Supponiamo di avere \(N\) documenti nella nostra collezione e supponiamo di aver già calcolato il ranking di ciascun documento. Andiamo adesso a discutere come gli steps (II) e (III) possono essere effettuati nello stesso momento tramite l'utilizzo di specifiche strutture dati.

L'idea è quella di utilizzare una coda di priorità per andare a selezionare direttamente i \(K\) documenti con il rank più alto, senza dover effettuare un completo sort di tutti i documenti. Questa differenza ha un forte impatto sulle performance, in quanto ordinare \(N\) elementi ha un costo di \(\Omega(N \cdot \log N)\), che è tipicamente molto più alto rispetto a quanto costerebbe selezionare solamente i \(K\) documenti con il rank più alto.

Consideriamo ad esempio la struttura heap, che ci permette di implementare una coda di priorità utilizzando un albero binario in cui ogni nodo ha un particolare valore, e i valori dei vari nodi sono ordinati in modo decrescente rispetto alla relazione padre-figlio, nel senso che il valore del padre è sempre maggiore del valore dei figli.

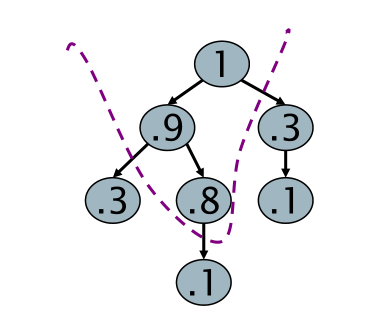
Utilizzando una heap, che può essere costruita in tempo lineare \(O(N)\), siamo in grado di leggere i \(K\) documenti con il ranking più alto in \(O(\log K)\) passi, il che è molto, molto più veloce rispetto a quanto richiesto da un sorting completo.

Il vero bottleneck della computazione risulta quindi essere lo step (I), ovvero il calcolo della cosine similarity. Per rendere più efficiente questo step l'idea potrebbe essere quella di calcolare il ranking solo su un campione scelto dei documenti, e non sull'intera collezione di documenti.

La scelta di calcolare la cosine similarity solo su alcuni documenti introduce però la possibilità che nei \(K\) documenti che ritorniamo potrebbe finire un documento che rispetto all'intera collezione non si trova nelle prime \(K\) posizioni. Parliamo di safe ranking quando un metodo ci garantisce che i \(K\) documenti ritornati sono effettivamente i primi \(K\) documenti che massimizzano il ranking rispetto all'intera collezione documentale.

I metodi che seguono non sempre sono safe. Anzi, tendenzialmente non sono safe, in quanto per ottimizzare la computazione finiscono col perdere dei documenti. Questo fatto però non è poi così distruttivo come può sembrare.

L'idea di questo metodo, che prende il nome di index elimination, è quella di considerare nel calcolo della cosine similarity solamente i documenti che contengono almeno un termine presente nella query. Questa idea base può poi essere estesa nei seguenti modi:

• Si può considerare nel calcolo del ranking solo i termini della query con un alto valore di \(\text{idf}\). Ad esempio nella query

  \[\text{catcher in the rye}\]

  possiamo intuire che l'eventuale presenza dei termini \(\text{in}\) e \(\text{the}\) nei documenti non andrà ad incrementare di molto il loro score, in quanto sono termini molto frequenti. L'idea è quindi quella di considerare solo i termini più significativi \(\text{catcher}\) e \(\text{rye}\). Così facendo non dobbiamo considerare le posting lists dei termini con un basso livello di \(\text{idf}\), che tipicamente sono abbastanza grandi.

• Un'altra possibile estensione è quella di considerare solamente i documenti che contengono tanti termini della query.

Queste strategie possono essere mischiate tra loro. L'importante in ogni caso è fare in modo che l'insieme dei contenders sia piccolo rispetto all'insieme di tutti i documenti, ma sia comunque significativo rispetto agli effettivi \(K\) documenti con il massimo rank.

L'idea è quella di pre-calcolare per ogni termine del dizionario \(t\) la lista degli \(r\) documenti con il peso maggiore nella posting list di \(t\). Questa lista è chiamata la champion list per il termine \(t\).

Il valore \(r\) deve essere scelto nel momento in cui iniziamo ad indicizzare i documenti. Può dunque succedere che \(r < K\).

Quando dobbiamo rispondere ad una query si calcola lo score solamente per i documenti presenti nella champion list di alcuni dei termini presenti nella query. Da questi vengono calcolati e ritornati i top \(K\) docs.

Fino a questo momento nel calcolo del ranking abbiamo sempre e solo considerato la rilevanza del documento rispetto alla query. C'è però un altro aspetto importate da tenere a mente: l'autorità del documento rispetto all'intera collezione documentale. Quest'ultima quantità tipicamente è una proprietà del documento indipendente dalla particolare query a cui vogliamo rispondere.

Mentre abbiamo modellato la rilevenza tramite la cosine similarity, per modellare l'autorità di un documento \(d\) possiamo utilizzare un numero nell'intervallo \([0, 1]\), detto quality score e denotato con il simbolo \(g(d)\). A seconda del contesto in cui ci muoviamo, ci sono vari segnali che possiamo utilizzare per calcolare questo \(g(d)\). Tra questi troviamo:

• Citazioni di un articolo scientifico;

• Valore del pagerank (trattato verso la fine del corso);

• Quantità di interazione da parte degli utenti come "mi piace" o "bookmarks".

L'idea è quindi quella di combinare il valore statico dell'autorità con quello dinamico della rilevanza per ottenere un net score del documento. La combinazione più semplice è la seguente

\[\text{net-score}(q, d) = g(d) + \text{cosine}(q, d)\]

Possiamo poi utilizzare questo net-score per ordinare i documenti e ritornare i primi \(K\) docs.

Osservazione: Questo metodo può anche essere combinato con l'utilizzo delle champion lists. In particolare si mantiene per ogni termine una champion list con i primi \(r\) docs che massimizzano \(g(d) + \text{tf-idf}_{t,d}\).

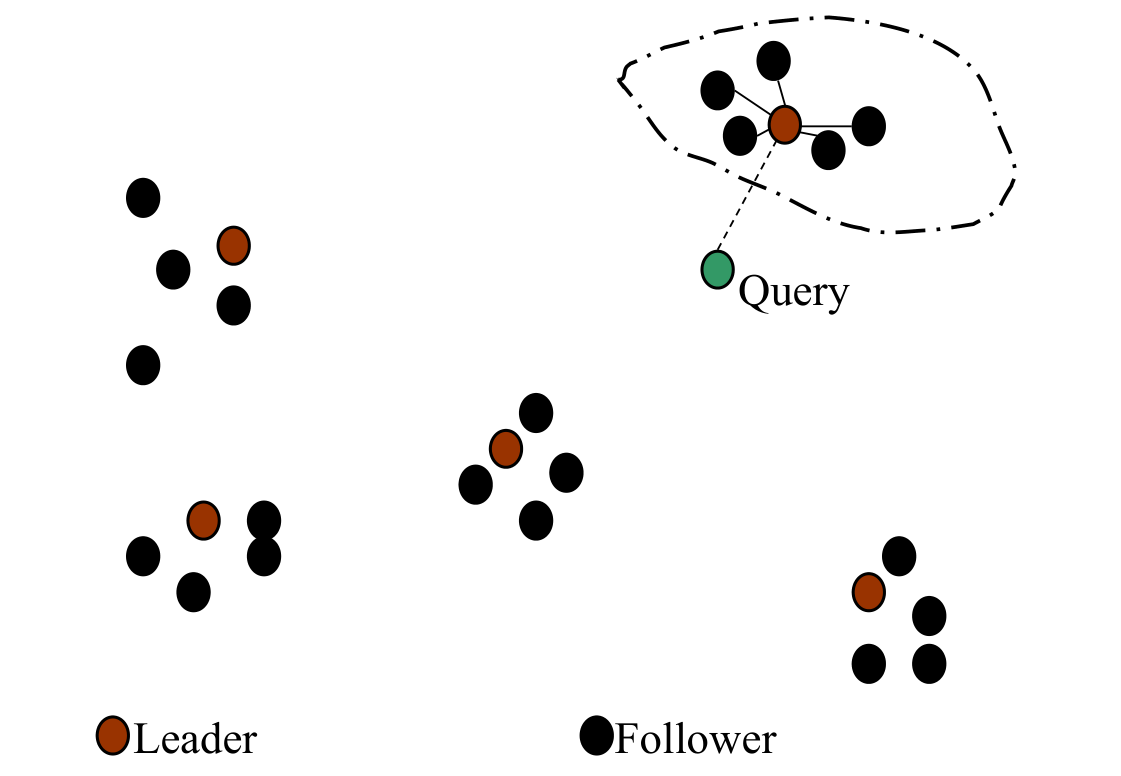
L'idea del cluster pruning è quella di scegliere in modo uniforme \(\sqrt{N}\) documenti dalla collezione. Questi saranno i leaders, mentre i restanti documenti sono i followers. Per ogni follower quindi ci si calcola il documento leader più vicino. Così facendo molto probabilmente ogni leader avrà \(\approx \sqrt{N}\) followers.

Il processo di risposta ad una query avviene nel seguente modo:

• Data una query \(Q\) troviamo il leader \(L\) più vicino a \(Q\);

• Prendiamo i \(K\) docs più vicini a \(q\) tra i followers di \(L\).

Graficamente troviamo

L'idea è quella di mantenere per ogni termine \(t\) due posting lists, una chiamata high e l'altra low. Possiamo pensare alla posting list high come se fosse una champion list. Quando necessitiamo di attraversare le posting lists di \(t\), andiamo prima in quella high. Se troviamo più di \(K\) docs ci fermiamo, altrimenti procediamo in quella low.

Volendo astrarre, l'idea generale è quella di spezzare le posting lists dell l'indice inverso in una gerarchia di posting lists, dalla più importante alla meno importante. Per fare questo si possono utilizzare sia valori statici come \(g(d)\) e sia altre misure. Quando poi dobbiamo rispondere ad una query esploriamo le posting lists di un termine \(t\) da quella più importante fino a quella meno importante, e ci fermiamo non appena abbiamo trovato più di \(K\) documenti.

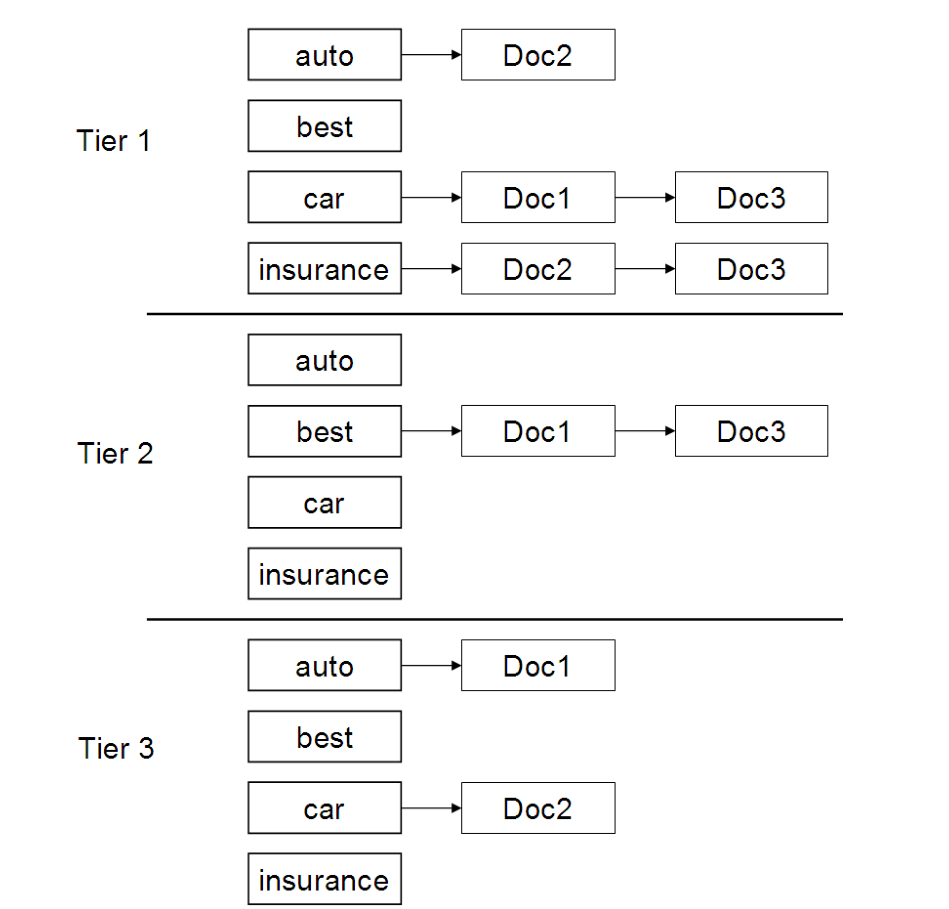
L'idea è quella di ordinare le posting lists del termine \(t\) utilizzando la frequenza del termine nel documento \(\text{wf}_{t,d}\). Per scegliere i documenti su cui calcolare la cosine similarity o altre misure di ranking abbiamo poi due approcci:

• Early termination: Ci fermiamo o dopo avere visto su un certo numero \(r\) di documenti, oppure quando la frequenza \(\text{wf}_{t,d}\) scende sotto un fissato valore di threshold. Una volta fermati calcoliamo il ranking sull'unione dei documenti che abbiamo visto.

• idf-ordered items: L'idea è quella di considerare i termini della query in ordine decrescente rispetto alla \(\text{idf}\). Infatti i termini con un alto valore di \(\text{idf}\) sono quelli che tipicamente hanno un maggiore contributo rispetto allo score finale. Smettiamo il processo quando vediamo che i termini della query che stiamo considerando non fanno cambiare di molto il ranking dei documenti.

Il WAND (Weak-AND) scoring è un ranking di tipo DAAT (Document-At-A-Time).

L'idea alla base del WAND è di avere le posting lists ordinate rispetto ai vari \(\text{docIDs}\) e di poter utilizzare un iteratore speciale che, dato un valore \(x\), ci permette di muoverci all'interno della posting list al primo \(\text{docID} > x\).

Durante la computazione abbiamo un finger (puntatore) per ogni termine che punta in una qualche posizione nella posting list del termine. Ogni finger si può muovere solamente a destra su dei \(\text{docIDs}\) più alti. Durante l'intera durata della computazione poi si mantiene la seguente proprietà invariante: tutti i \(\text{docIDs}\) più piccoli di qualsiasi finger sono già stati processati.

Questa procedura utilizza i valori di \(\text{tf}\) e \(\text{idf}\) assieme ad un valore di threshold per eliminare in modo safe i documenti che non riusciranno mai ad arrivare nei top \(K\). Per fare questo in ogni momento e per ogni termine \(t\) ci si memorizza un upper bound \(\text{UB}_t\) che rappresenta il massimo contributo che può avere un doc che si trova alal destra del finger associato a \(t\).

Utilizzando questi valori di upper bound si è in grado di capire se è possibile o meno superare il valore di threshold.

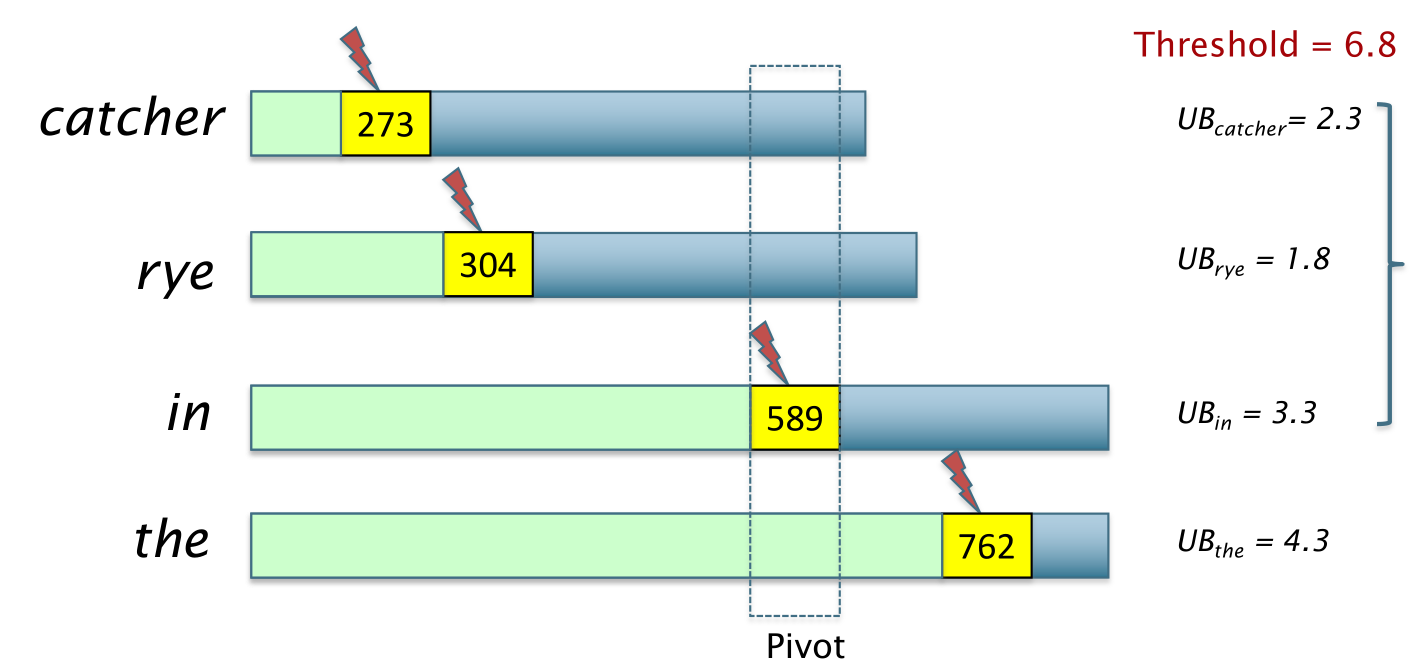
Nel caso in cui si capisce che non si riesce a superare la threshold, si è in grado di eliminare i documenti che sappiamo sicuramente non appartengono nei top \(K\).

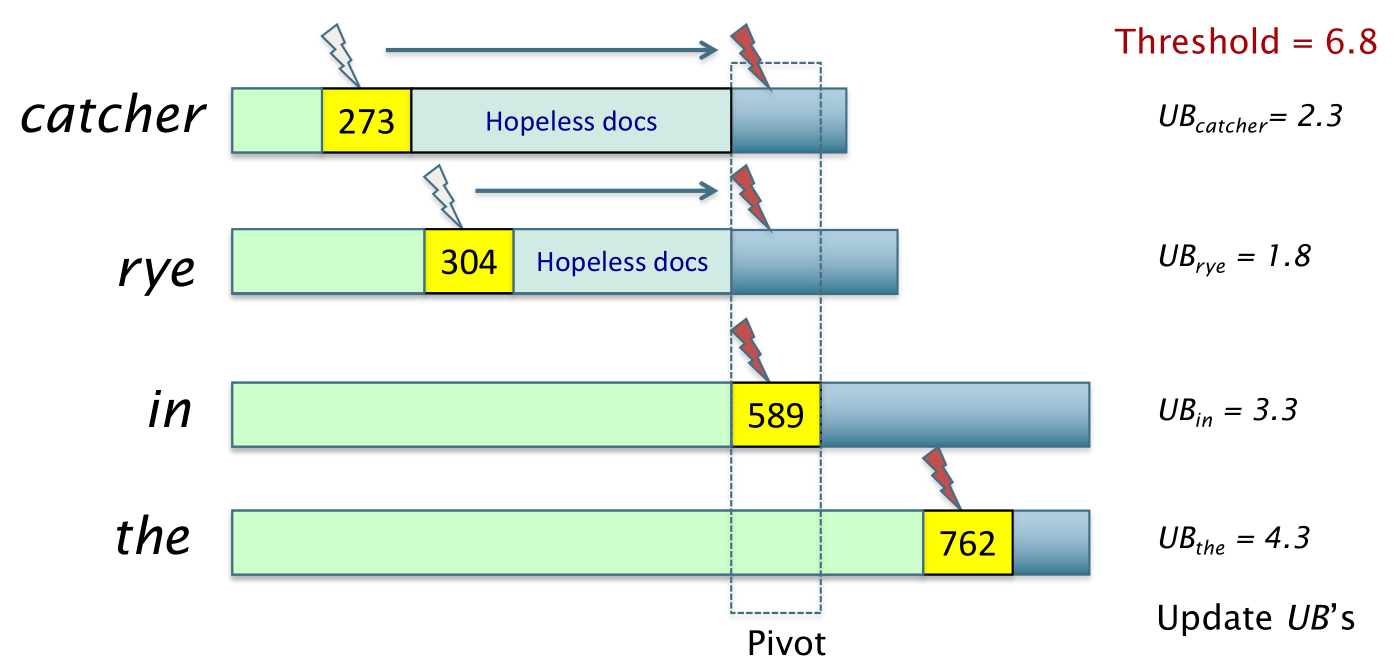
In tal caso quindi tramite l'iteratore siamo in grado di scartare tali documenti e passare al documento pivot, che rappresenta il documento che ci permette potenzialmente di superare il threshold.

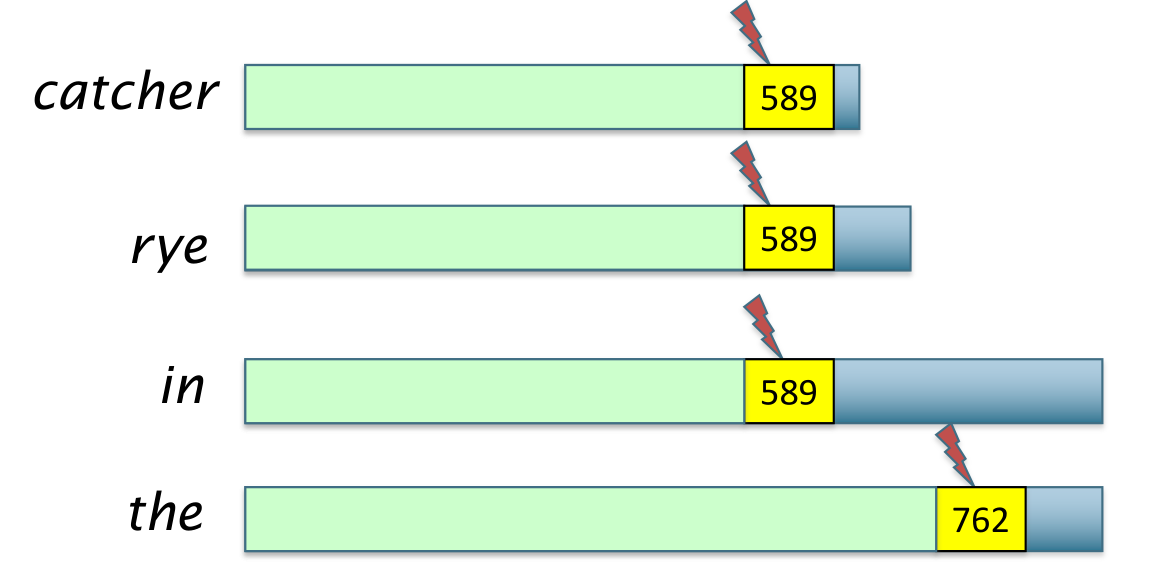
Tramite l'utilizzo di questa procedura si possono ottenere dei grandi benefici dal punto di vista di risorse computazionali utilizzate. Questo metoodo inoltre è molto generale, e può essere applicato per tutte le funzioni di ranking che sono additive by term.