ISTI - Esercizio 2

Date \(X, Y \sim U[0, \theta]\), calcolare la distribuzione di \(U := X + Y\).

---

[2020-06-25 gio 14:11]

Iniziamo notando che

\[\begin{split} F_U(t) &= P(U \leq t) \\ &= P(Y + X \leq t) \\ &= P(Y \leq -X + t) \end{split}\]

osserviamo poi che \(U\) non può assumere valori negativi, in quanto sia \(X\) che \(Y\) sono \(\geq 0\), e dunque anche la loro somma è \(\geq 0\). Questo significa che \(F_U(t) = 0\) per \(t < 0\). Andiamo adesso ad analizzare il restante caso in cui \(t \geq 0\).

L'idea è quella di rappresentare la regione del piano che contribuisce al valore di probabilità dell'evento \(\{Y \leq -X + t\}\). A seconda della relazione tra \(t\) e \(\theta\) possiamo avere tre particolari casi, che andiamo a discutere a seguire.

• Caso 1: \(\theta \geq t\)

  In questo caso troviamo il seguente grafico

  

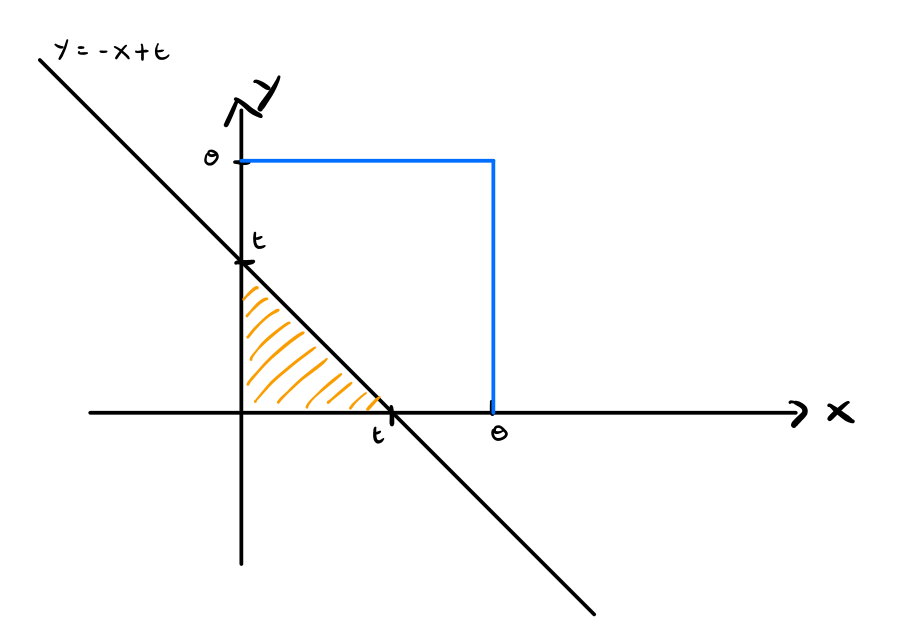
  notiamo che i punti \((x_0, y_0)\) che si trovano all'interno del quadrato blu sono i punti in cui la densità congiunta è maggiore di \(0\), \(f(x, y) > 0\). I punti contenuti nell'area in arancione sono invece i punti che contribuiscono all'evento a cui siamo interessati.

  Dato che \(X\) e \(Y\) sono i.i.d., abbiamo che la loro densità congiunta è data da

  \[f(x, y) = f(x) \cdot f(y) = \frac{1}{\theta} \cdot \frac{1}{\theta} = \frac{1}{\theta^2}\]

  La probabilità a cui siamo interessati può quindi essere calcolata tramite il seguente integrale doppio

  \[\begin{split} P(Y \leq -X + t) &= \int\limits_{x = 0}^t \int\limits_{y = 0}^{-x + t} \frac{1}{\theta^2} \,\, dy \, dx\\ &= \int\limits_{x = 0}^t \frac{1}{\theta^2} \cdot (-x + t) \,\, dx \\ &= \int\limits_{x = 0}^t - \frac{x}{\theta^2} + \frac{t}{\theta^2} \,\, dx \\ &= \Big[ -\frac{x^2}{2\theta^2} + \frac{tx}{\theta^2} \;\; \underset{x=0}{\overset{x=t}{|}} \; \Big] \\ &= -\frac{t^2}{2 \theta^2} + \frac{t^2}{\theta^2} \\ &= \frac{t^2}{2\theta^2} \\ \end{split}\]

• Caso 2: \(\theta \leq t \leq 2\theta\)

  Questo caso è leggermente più complesso, in quanto abbiamo la seguente figura

  

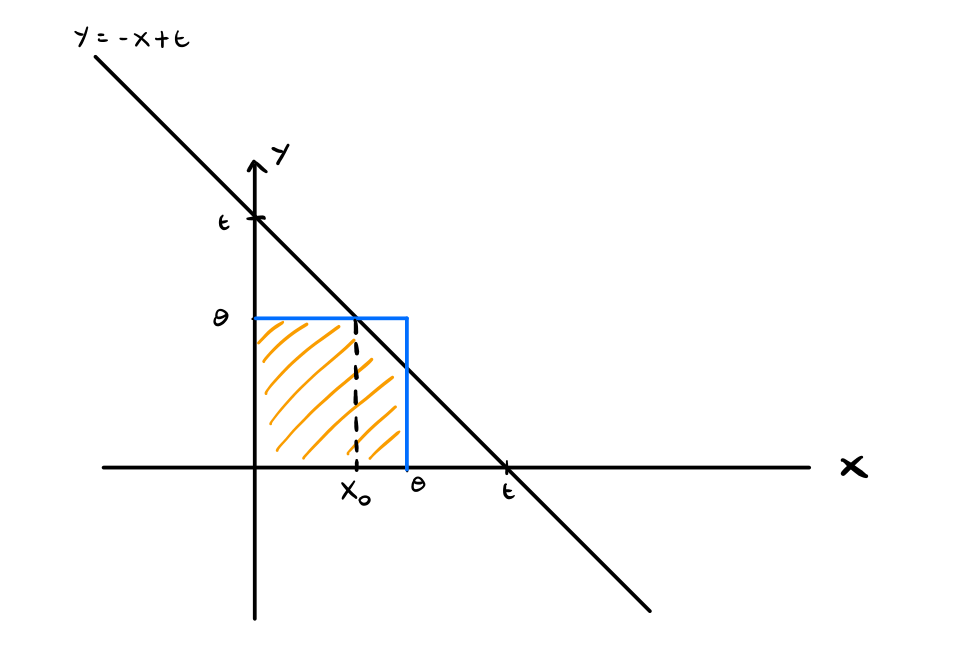
  come è possibile vedere infatti l'area a cui siamo interessati può essere spezzata in due parti, con punto di "rottura" il valore \(x_0\) tale che

  \[-x_0 + t = \theta \iff x_0 = t - \theta\]

  questo significa che la probabilità a cui siamo interessati può essere calcolata tramite i seguenti integrali doppi

  \[P(Y \leq -X + t) = \int\limits_{x = 0}^{t - \theta} \int\limits_{y = 0}^{\theta} \frac{1}{\theta^2} \,\, dydx + \int\limits_{x = t - \theta}^{\theta} \int\limits_{y = 0}^{-x + t} \frac{1}{\theta^2} \,\, dy dx\]

  che andandoli a calcolare ci danno

  \[\begin{split} \int\limits_{x = 0}^{t - \theta} \int\limits_{y = 0}^{\theta} \frac{1}{\theta^2} \,\, dydx &= \int\limits_{x = 0}^{t - \theta} \frac{1}{\theta} \,\, dx \\ &= \frac{1}{\theta} \cdot x \;\; \underset{x=0}{\overset{x=t - \theta}{|}} \;\\ &= \frac{t - \theta}{\theta} \\ \end{split}\]

  e

  \[\begin{split} \int\limits_{x = t - \theta}^{\theta} \int\limits_{y = 0}^{-x + t} \frac{1}{\theta^2} \,\, dy dx &= \int\limits_{x = t - \theta}^{\theta} \frac{y}{\theta^2} \;\; \underset{y=0}{\overset{y=-x + t}{|}} \; \,\, dx \\ &= \int\limits_{x = t - \theta}^{\theta} \frac{-x}{\theta^2} + \frac{t}{\theta^2} \,\, dx \\ &= -\frac{x^2}{2\theta^2} + \frac{xt}{\theta^2} \underset{y=t - \theta}{\overset{y=\theta}{|}} \\ &= \frac{-\theta^2}{2\theta^2} + \frac{\theta t}{\theta^2} + \frac{(t - \theta)^2}{2\theta^2} - \frac{(t - \theta)t}{\theta^2} \\ &= -\frac12 + \frac{t}{\theta} + \frac{(t-\theta)^2}{2\theta^2} - \frac{(t-\theta)t}{\theta^2} \\ \end{split}\]

  Sommando i due risultati troviamo quindi la seguente espressione

  \[P(Y \leq -X + t) = \frac{t - \theta}{\theta} -\frac12 + \frac{t}{\theta} + \frac{(t-\theta)^2}{2\theta^2} - \frac{(t-\theta)t}{\theta^2}\]

• Caso 3: \(t > 2\theta\)

  Per questo ultimo caso invece abbiamo la seguente situazione

  

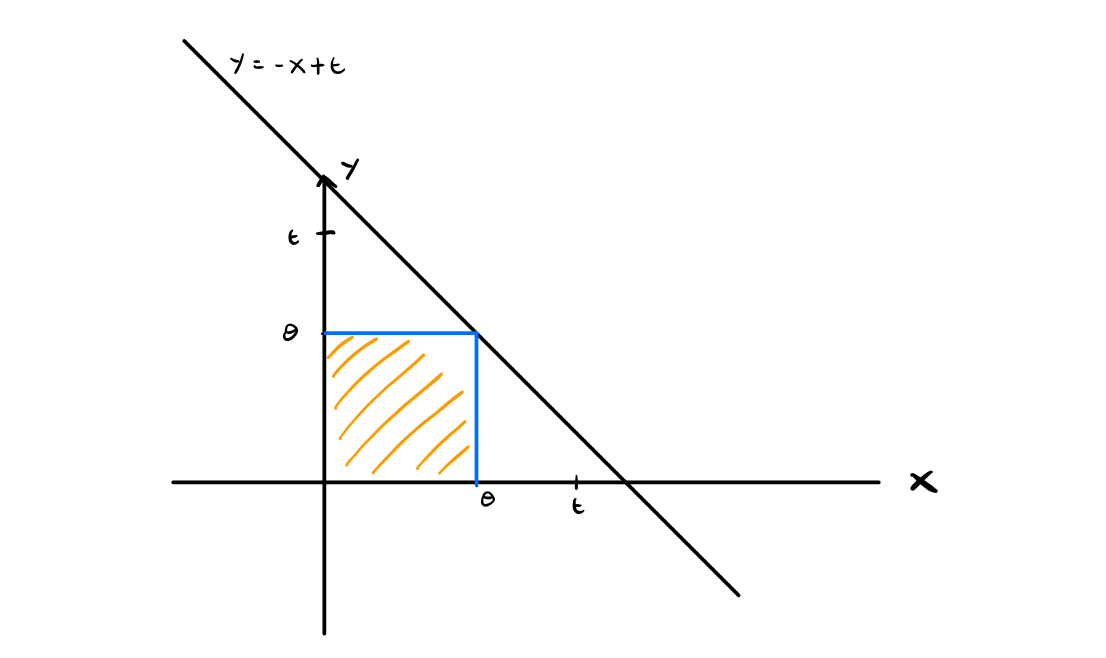
  in particolare la probabilità di interesse è data da

  \[P(Y \leq -X + t) = \int\limits_{x = 0}^{\theta} \int\limits_{y = 0}^{\theta} \frac{1}{\theta^2} \,\, dy \, dx = 1\]

Mettendo assieme tutti i casi troviamo la seguente espressione per la distribuzione di \(U\)

\[F_U(t) = \begin{cases} \displaystyle{\frac{t^2}{2\theta^2}} \,\,\,&, \,\,\, 0 < t < \theta \\ \\ \displaystyle{\frac{t - \theta}{\theta} -\frac12 + \frac{t}{\theta} + \frac{(t-\theta)^2}{2\theta^2} - \frac{(t-\theta)t}{\theta^2}} \,\,\,&, \,\,\, \theta \leq t < 2\theta \\ \\ 1 \,\,\,&, \,\,\, t \geq 2\theta \\ \end{cases}\]

\[\tag*{$\checkmark$}\]