ISTI - Esercizio 3
Traccia
Date \(X, Y \sim \mathcal{N}(0, 1)\) indipendenti tra loro, trovare la distribuzione di \(U := \frac{Y}{X}\).
Svolgimento
Iniziamo notando che
\[\begin{split} F_U(t) &= P(U \leq t) \\ &= P(\frac{Y}{X} \leq t) \\ &= P(\{Y \leq X \cdot t, \,\, X \geq 0\} \cup \{Y \geq X \cdot t, \,\, X < 0\}) \\ \end{split}\]
inoltre, dal fatto che \(X\) e \(Y\) sono indipendenti, segue che la loro densità congiunta è data da
\[f(x, y) = f_X(x) \cdot f_Y(y) = \frac{1}{2\pi} e^{-\frac12(x^2 + y^2)}\]
Il resto dell'analisi è spezzata in due casi, a seconda del valore di \(t\).
- Caso 1: \(t > 0\)
In questo caso troviamo la seguente zona di interesse, colorata di arancione
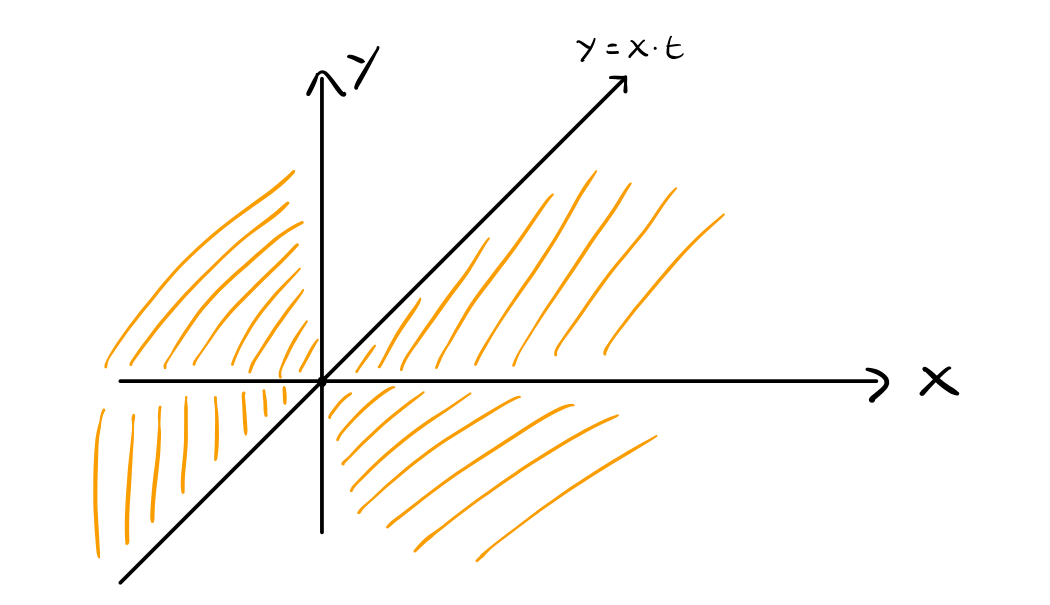
al fine di calcolare la probabilità di interesse utilizziamo le coordinate polari. Inoltre, dato che la funzione \(f(x, y)\) è una funzione radialmente simmetrica, ci basta calcolare il volume di una sola delle due sezioni e moltiplicare il valore trovato per due per ottenere il volume totale. Troviamo quindi
\[\begin{split} \iint\limits_D f(x, y) \,\, dy\,dx &= 2 \cdot \int\limits_{\theta = -\frac{\pi}{2}}^{\arctan(t)} \int\limits_{r = 0}^{+\infty} \frac{1}{2\pi} e^{-\frac12 r^2} r \,\, dr\,d\theta\\ &= 2 \frac{1}{2\pi} \Big[ \arctan(t) + \frac{\pi}{2} \Big] \\ &= \frac{\arctan(t)}{\pi} + \frac12 \\ \end{split}\]
- Caso 2: \(t < 0\)
In questo caso il grafico è il seguente
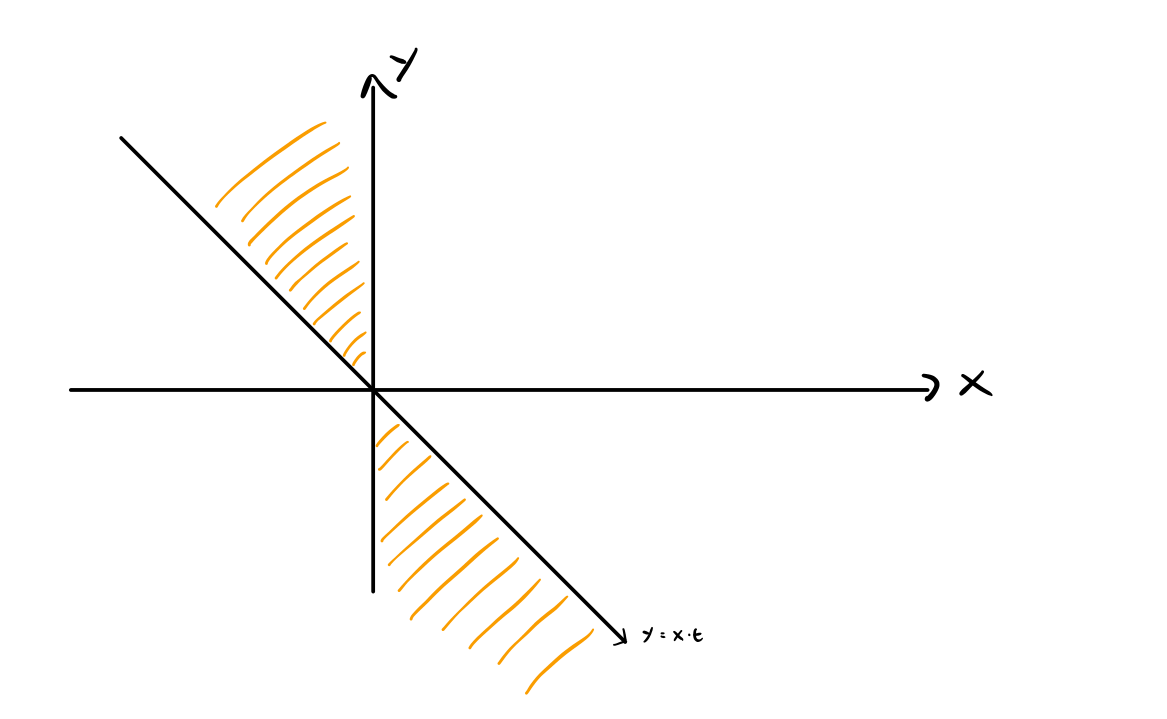
Nuovamente, possiamo utilizzare il cambio in coordinate polari e la simmetria radiale di \(f(x, y)\) per semplificare i calcoli e ottenere
\[\begin{split} P(U \leq t) = \iint_D \frac{1}{2\pi} e^{-\frac12(x^2 + y^2)} \,\, dy\,dx &= 2 \cdot \int\limits_{\theta = \frac{\pi}{2}}^{\pi + \arctan(t)} \int\limits_{r = 0}^{+\infty} \frac{1}{2\pi} e^{-\frac12 r^2} r \,\, dr d\theta \\ &= \frac{1}{\pi} \cdot \Big[ \pi + \arctan(t) - \frac{\pi}{2} \Big] \\ &= \frac{\arctan(t)}{\pi} + \frac12 \\ \end{split}\]
Dato che in entrambi i casi abbiamo la stessa espressione, mettendo tutto assieme troviamo
\[\forall t \in \mathbb{R}: \,\,\, F_U(t) = \frac{\arctan(t)}{\pi} + \frac12\]
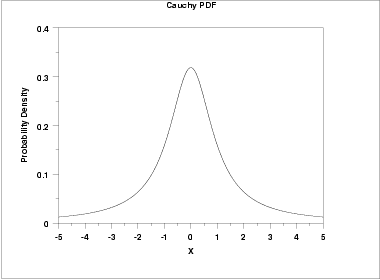
notiamo quindi come \(U\) abbia una distribuzione di Cauchy centrata nell'origine.
\[\tag*{$\checkmark$}\]
Osservazione: La densità della distribuzione di Cauchy è simile alla tipica forma a campana della densità normale con una minore concentrazione rispetto al valore medio. Per via di questa mancanta concentrazione dei valori la distribuzione di Cauchy è caratterizzat dal fatto di non avere un valore atteso finito. Segue una immagina della densità della distribuzione di Cauchy