ISTI - 01 - Concetti Base I

Consideriamo ora la seguente v.a. \(Y = g(X)\). Il valore atteso di \(Y\), utilizzando la definizione appena data, è dato dal seguente integrale

\[\mathbb{E}[Y] = \int_{-\infty}^{\infty}{y \cdot f_y(y) \,\,\, dy}\]

al fine di calcolare tale integrale effettuiamo il cambio di variabili \(y = g(x)\), che ci permette di ottenere

\[\frac{g(x)}{dx} = \frac{dy}{dx} \iff g'(x) = \frac{dy}{dx} \iff dy = g'(x) \,\, dx\]

sostituendo nell'integrale di prima otteniamo quindi

\[\begin{split} \mathbb{E}[Y] &= \int_{-\infty}^{\infty}{y \cdot f_y(y) \,\, dy} \\ &= \int_{-\infty}^{\infty} {g(x) \cdot f_y(g(x)) \cdot g'(x) \,\, dx} \\ \end{split}\]

utilizzando la formula precedentemente dimostrata troviamo che

\[f_y(g(x)) = \frac{f_x(g^{-1}(g(x)))}{g^{'}(g^{-1}(g(x)))} = \frac{f_x(x)}{g^{'}(x)}\]

continuando quindi il calcolo dell'integrale otteniamo

\[\begin{split} \mathbb{E}[Y] &= \int_{-\infty}^{\infty} {g(x) \cdot f_y(g(x)) \cdot g'(x) \,\, dx} \\ &= \int_{-\infty}^{\infty} {g(x) \cdot \frac{f_x(x)}{g^{'}(x)} \cdot g^{'}(x) \,\, dx} \\ &= \int_{-\infty}^{\infty} {g(x) \cdot f_x(x) d_x} \\ &= \mathbb{E}[g(X)] \\ \end{split}\]

Riassumendo, abbiamo dimostrato che se \(Y = g(X)\), allora

\[\mathbb{E}[Y] = \mathbb{E}[g(X)]\]

e quindi ci basta conoscere la densità di \(X\) per poter calcolare la media di una funzione di \(X\), come \(Y = g(X)\).

Un'altra formula utile nel calcolo dei momenti, ovvero delle media, è la seguente

\[\mathbb{E}[X^2] = \int_{-\infty}^{\infty} x^2 f_x(f) \,\, dx\]

Esiste un modo alternativo per calcolare la varianza, che è ottenuto utilizzando la proprietà di linearità del valore atteso nel seguente modo

\[ \begin{split} Var[X] &= \mathbb{E}[ (X - \mathbb{E}[X]) ^2 ] \\ &= \mathbb{E}[ X^2 - 2X\mathbb{E}[X] + \mathbb{E}[X]^2 ] \\ &= \mathbb{E}[X^2] - \mathbb{E}[2X\mathbb{E}[X]] + \mathbb{E}[\mathbb{E}[X]^2] \\ &= \mathbb{E}[X^2] - 2\mathbb{E}[X]^2 + \mathbb{E}[X]^2 \\ &= \mathbb{E}[X^2] - \mathbb{E}[X]^2 \\ \end{split}\]

Sia \((\Omega, F, P)\) uno spazio di probabilità, e sia \(A \in F\) un particolare evento. Indichiamo con \(1_A\) la funzione indicatrice dell'evento \(A\), ovvero la funzione \(1_A: \Omega \to \Omega\) definita come segue

\[\forall \omega \in \Omega: \,\, 1_A(\omega) = \begin{cases} 1 \,&,\, \omega \in A \\ 0 \,&,\, \omega \not \in A \\ \end{cases}\]

Notiamo che la densità discreta di \(1_A\) è data da

\[p(x) = \begin{cases} P(1_A = 0) = 1 - P(A) \,\,&,\,\, x = 0 \\ P(1_A = 1) = P(A) \,\,&,\,\, x = 1 \\ P(1_A = x) = 0 \,\,&,\,\, x \neq 0, 1 \\ \end{cases}\]

La distribuzione binomiale viene utilizzata per contare il numero di successi in uno schema di Bernoulli in cui si effettuano \(n\) prove indipendenti, ciascuna delle quali ha probabilità di successo \(p\) e probabilità di insuccesso \(1-p\).

Formalmente indichiamo una v.a. con distribuzione binomale con \(X \sim Bin(n, p)\). La densità di una v.a. con distribuzione binomiale è quindi la seguente

\[\forall k \in \{0, ..., n\}: \,\, p(k) = P(X = k) = \binom{n}{k} p^k (1-p)^{n-k}\]

Per quanto riguarda valore atteso e varianza, abbiamo che

• \(\mathbb{E}[X] = n \cdot p\)

• \(Var[X] = n \cdot p \cdot (1-p)\)

La distribuzione geometrica viene utilizzata per contare il numero di fallimenti necessari per ottenere il primo successo, assumendo di poter fare infinite prove di un esperimento in cui la probabilità di successo è \(p\) e la probabilità di insuccesso è \(1-p\).

Formalmente indichiamo una v.a. con distribuzione geometrica con \(X \sim Ge(p)\). La densità di tale v.a. è data da

\[p(k) = \begin{cases} p\cdot(1-p)^k \,\,&,\,\, k \geq 0 \\ 0 \,\,&,\,\, \text{ altrimenti } \\ \end{cases}\]

Per quanto riguarda valore atteso e varianza, abbiamo che

• \(\mathbb{E}[X] = \displaystyle{\frac{1}{p}}\)

• \(Var[X] = \displaystyle{\frac{1-p}{p^2}}\)

Una v.a. che segue la distribuzione di Poisson è indicata con \(X \sim Poisson(\lambda)\), con \(\lambda > 0\) parametro della distribuzione. Tale v.a. ha la seguente densità

\[p(k)=\begin{cases} \displaystyle{e^{-\lambda} \cdot \frac{\lambda^k}{k!}} \,\,&,\,\, k = 0,1,2,... \\ 0 \,\,&,\,\, \text{ altrimenti } \end{cases}\]

Notiamo che si tratta di una densità di probabilità in quanto, dallo sviluppo di Taylor, segue che

\[e^{\lambda} = \sum\limits_{k = 0}^{\infty} \frac{\lambda^k}{k!}\]

Per quanto riguarda valore atteso e varianza, abbiamo che

• \(\mathbb{E}[X] = \lambda\)

• \(Var[X] = \lambda\)

Una v.a. continua \(X\) è detta uniforme in \([a, b]\), in simboli \(X \sim U[a, b]\), se la probabilità che \(X\) assuma valori in un sottointervallo \([c, d]\) di \([a, b]\) dipende solamente dall'ampiezza del sottointervallo, e non da dove esso è collocato.

Tale variabile aletoria ha la seguente funzione di ripartizione

\[F_X(t) = \begin{cases} 0 \,&,\,\, t < a \\ \\ \displaystyle{\frac{t-a}{b-a}} \,&,\,\, a \leq t \leq b \\ \\ 1 \,&,\,\, t > b \\ \end{cases}\]

Dato che \(F_X(t)\) è continua e derivabile con derivata continua in tutto l'intervallo tranne che in \(0\) e \(1\), abbiamo che è possibile ottenere una densità di \(X\) andando a derivare \(F_X(t)\) e ottenendo

\[f_X(t) = \begin{cases} \displaystyle{\frac{1}{b-a}} \,&,\,\, a < t < b \\ \\ 0 \,&,\,\, \text{ altrimenti } \\ \end{cases}\]

Notiamo che, dati \(U \sim U[0,1]\) e \(a,b \in \mathbb{R}\), allora

\[Y = a + b \cdot U \sim U[a, a + b]\]

Una v.a. continua \(X\) è detta esponenziale con parametro \(\lambda\), in simboli \(X \sim Exp(\lambda)\), se ha la seguente densità

\[f_X(t) = \begin{cases} \lambda e^{-\lambda t} \,&,\,\, t > 0 \\ 0 \,&,\,\, \text{ altrimenti } \\ \end{cases}\]

La funzione di ripartizione è invece la seguente

\[F_X(t) = \begin{cases} 1 - e^{-\lambda t} \,&,\,\, t \geq 0 \\ 0 \,&,\,\, \text{ altrimenti } \\ \end{cases}\]

Una v.a. continua \(X\) è detta normale con parametri \(\mu, \sigma\), in simboli \(X \sim \mathcal{N}(\mu, \sigma^2)\), se ha la seguente densità

\[f_X(t) = \phi(t) = \frac{1}{\sigma \sqrt{2\pi}} \cdot e^{\displaystyle{-\frac12 \Big( \frac{x - \mu}{\sigma} \Big)^2}}\]

Graficamente quindi la densità normale è rappresentata come segue

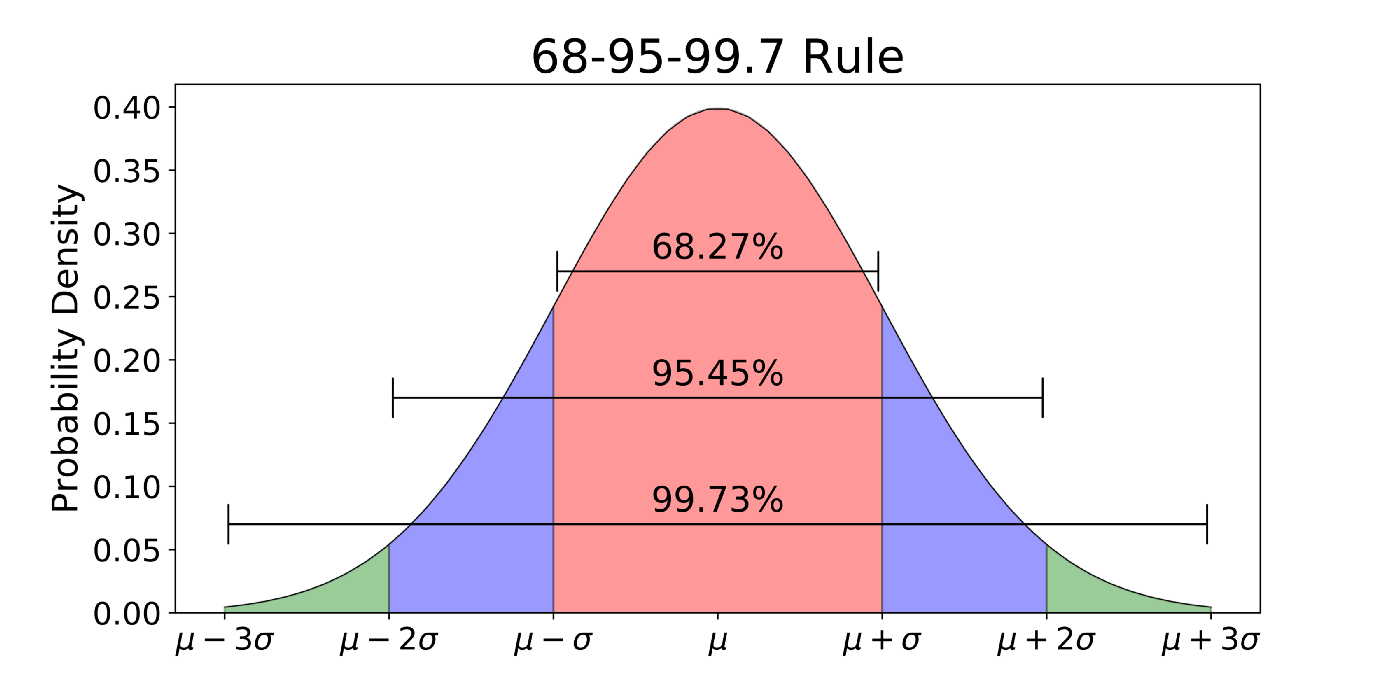
Notiamo che non è possibile esprimere la funzione di ripartizione per una v.a. normale con una funzione primitiva, in quanto è definita come segue

\[\Phi(t) := \int\limits_{-\infty}^t \phi(t) \, dt\]

Nel caso in cui \(\mu = 1\) e \(\sigma^2 = 0\), allora abbiamo a che fare con una v.a. normale standard.

La densità della distribuzione gamma è denotata con \(\Gamma(k, \lambda)\), dove \(k\) e \(\lambda\) sono i parametri della distribuzione, ed è definita dalla seguente formula

\[f(x) := \begin{cases} \displaystyle{\frac{\lambda^k x^{k-1} e^{-\lambda x}}{\Gamma(k)}} &, x > 0 \\ 0 &, x \leq 0 \\ \end{cases}\]

dove con \(\Gamma(k)\) si intende la funzione gamma, definita da

\[\Gamma(k) := \int\limits_{0}^{\infty} s^{x-1}e^{-x} ds\]

Graficamente otteniamo la seguente forma

Le origini della funzione gamma sono molto interessanti. Inizialmente la funzione gamma è stata definita per estendere la funzione fattoriale \(n!\) all'insieme dei valori reali. Notiamo infatti che utilizzando la tecnica di integrazione per parti

\[\int fg = F g - \int F g^{'} \,\,\, \text{, con } F \text{ primitiva di } f\]

è possibile far vedere che \(\forall x \in \mathbb{N}\)

\[\Gamma(x) = (x-1)!\]

Andiamo adesso a calcolare il valore atteso della distribuzione Gamma. Data la v.a. \(X \sim \Gamma(k, \lambda)\), troviamo che

\[\begin{split} \mathbb{E}[X] &= \int\limits_{0}^{\infty} x \cdot \frac{\lambda^k x^{k-1} e^{-\lambda x}}{\Gamma(k)} dx \\ &= \int\limits_{0}^{\infty} \frac{\lambda^{k} x^{k} e^{-\lambda x}}{\Gamma(k)} dx \\ &= \frac{\Gamma(k+1)}{\Gamma(k+1)} \cdot \frac{\lambda}{\lambda} \cdot \int_{0}^{\infty} \frac{\lambda^{k} x^{k} e^{-\lambda x}}{\Gamma(k)} dx \\ &= \frac{\Gamma(k+1)}{\Gamma(k)} \cdot \frac{1}{\lambda} \cdot \int_{0}^{\infty} \frac{\lambda^{k+1} x^{k} e^{-\lambda x}}{\Gamma(k+1)} dx \\ &= \frac{\Gamma(k+1)}{\Gamma(k)} \cdot \frac{1}{\lambda} \cdot 1 \\ &= \frac{k!}{(k-1)!} \cdot \frac{1}{\lambda} \\ &= \frac{k}{\lambda} \\ \end{split}\]

notiamo infatti che \(\displaystyle{\frac{\lambda^{k+1} x^{k} e^{-\lambda x}}{\Gamma(k+1)}}\) è la densità di una \(\Gamma(k+1, \lambda)\), e dunque integrandola da \(0\) a \(\infty\) otteniamo \(1\) per definizione di densità di probabilità.

Il calcolo appena mostrato è un esempio di un fenomeno più generale. Molto spesso infatti troviamo delle formule che inizialmente ci possono sembrare difficili da calcolare, ma che alla fine si riducono ad essere densità di distribuzioni di probabilità. Utilizzando il fatto fondamentale che, se \(f(x)\) è una densità di probabilità, allora

\[\int\limits_{-\infty}^{\infty} x \cdot f(x) \,\,dx = 1\]

possiamo semplificare enormemente il calcolo di tali formule, per ottenere il risultato cercato.

La distribuzione chi-quadro è ottenuta prendendo delle normali standard e elevandole al quadrato. Quindi, se \(Z \sim \mathcal{N}(0, 1)\), allora \(Z^2 \sim \chi^2(1)\).

La somma di \(k\) v.a. indipendenti con distribuzione \(\chi^2(1)\), ovvero la distribuzione di \(k\) quadrati di normali standard \(\mathcal{N}(0,1)\) indipendenti si rappresenta con \(\chi^2(k)\), e viene chiamata distribuzione chi-quadro con k parametri di libertà.

Nel seguente esercizio abbiamo dimostrato che \(\chi^2(k)\) è una gamma di parametri \(\Gamma(k/2, 1/2)\). In particolare la sua pmf (probability mass function) è la seguente

\[\begin{split} F_Y(t) = 2\Phi(\sqrt{t}) - 1 \end{split}\]

mentre la sua pdf (probability density function) è la seguente

\[f_Y(t) = \frac{1}{\sqrt{2\pi}}t^{-1/2}e^{-t/2}\]

Seguono alcune informazioni sulla distribuzione chi-quadro: