ISTI - 02 - Concetti Base II
1 Lecture Info
Data:
In questa lezione abbiamo introdotto alcuni concetti statistici importanti utilizzati durante il corso.
2 Simulazione di Processi Stocastici
Una delle trasformazioni più importanti e utili che possiamo considerare data una variabile aleatoria \(X\) con funzione di distribuzione \(F_X(t) = P(X \leq t)\) è data proprio da \(F\). Infatti, posto \(Y = F(X)\), con \(F\) invertibile, abbiamo che
\[\begin{split} P(Y \leq t) &= P(F(X) \leq t) \\ &= P(X \leq F^{-1}(t)) \;\;\; \text{(F è monotona e non-decrescente)}\\ &= F(F^{-1}(t)) \\ &= t \end{split}\]
ovvero \(Y \sim U[0,1]\).
Notiamo poi che, se \(F\) rispetta determinate condizioni, è anche possibile invertire il processo appena mostrato. Supponiamo infatti che \(F\) sia invertibile, e consideriamo la sua inversa \(F^{-1}\). Sia \(U \sim U[0,1]\) e sia \(X := F^{-1}(U)\). Andiamo adesso a calcolare la distribuzione di \(X\)
\[\begin{split} P(X \leq t) &= P(F^{-1}(U) \leq t) \\ &= P(F(F^{-1}(U) \leq F(t)) \;\;\; \text{(F è monotona non decrescente)}\\ &= P(U \leq F(t)) \\ &= F(t) \end{split}\]
il che vuol dire che \(X\) ha proprio \(F\) come funzione di distribuzione.
Il ragionamento appena descritto ci dà un modo per simulare un qualsiasi v.a. con funzione di ripartizione \(F(t)\), supponendo di essere in grado di calcolare la funzione inversa \(F^{-1}\). Conoscendo \(F^{-1}\) infatti si ha che \(F^{-1}(U)\) è una v.a. con \(F\) come funzione di ripartizione.
Andiamo adesso a far vedere qualche esempio di simulazione di processi stocastici.
2.1 Esempio 1: Simulazione di \(Exp(\lambda)\)
Supponiamo di voler simulare una distribuzione esponenziale di parametro \(\lambda\), \(X \sim Exp(\lambda)\), utilizzando una v.a. \(U \sim U[0,1]\). Per iniziare ricordiamo che la funzione di distribuzione di una esponenziale di parametro lambda è data da
\[F_X(t) := \begin{cases} 1 - e^{-\lambda t} &, t > 0 \\ 0 &, t \leq 0 \\ \end{cases}\]
Sia \(t > 0\). Andiamo adesso a calcolare l'inversa di \(F_X(t)\).
\[\begin{split} y = 1 - e^{-\lambda t} &\iff 1 - y = e^{-\lambda t} \\ & \iff \ln{(1 - y)} = -\lambda t \\ &\iff t = -\frac{\ln{(1 - y)}}{\lambda} \end{split}\]
Per quanto visto prima, abbiamo quindi che
\[F^{-1}(U) = -\frac{\ln{(1-U)}}{\lambda} \sim X\]
osservando poi che, se \(U\) è uniforme in \([0, 1]\), allora anche \(1 - U\) è uniforme in \([0,1]\), abbiamo che
\[-\frac{\ln{U}}{\lambda} \sim Exp(\lambda)\]
2.2 Esempio 2: Simulazione di \(Bern(p)\)
Supponiamo adesso di voler simulare il lancio di una moneta che ottiene testa con probabilità \(p \in [0,1]\). Tale esperimento è modellato dalla distribuzione di Bernoulli, denotata con \(Bern(p)\).
Al fine di simulare una v.a. di bernoulli possiamo utilizzare una v.a. uniforme \(U \sim U[0,1]\) per poter definire la seguente variabile aleatoria discreta
\[X = \begin{cases} 1 &, \,\,U \leq p \\ 0 &, \,\,U > p \\ \end{cases}\]
Notiamo a questo punto che, per come è stata definita la v.a. \(X\), abbiamo che
\[ P(X = 1) = P(U \leq p) = p \]
in altre parole abbiamo che \(X \sim Bern(p)\).
2.3 Esempio 3: Simulazione di \(\mathcal{N}(0, 1)\)
Consideriamo adesso una v.a. \(X\) con distribuzione normale standard, \(X \sim \mathcal{N}(0,1)\). Ricordiamo che la densità di \(x\) è data da
\[\phi(t) := \frac{1}{\sqrt{2\pi}} \cdot e^{-\frac{t^2}{2}}\]
mentre la funzione di ripartizione è data da
\[\Phi(t) := \int\limits_{-\infty}^t \frac{1}{\sqrt{2\pi}} \cdot e^{-\frac{x^2}{2}} dx\]
Dato che non esiste una formula esplicita per \(\Phi(t)\), non esiste neanceh una formula esplicita per l'inversa, ovvero \(\Phi^{-1}(t)\). Dunque non è possibile utilizzare il metodo che abbiamo appena mostrato per simulare una normale standard utilizzando una uniforme in \([0,1]\).
In ogni caso, esistono comunque dei metodi empirici per calcolare in modo approssimato l'inversa, e dunque, volendo, anche per simulare una normale standard. Ad esempio, la trasformazione di Box-Muller, discussa in seguito, permette di simulare una coppia di v.a. con distribuzione normale.
3 Normalizzazione di una v.a. Normale
Sia \(Z\) una variabile aleatoria con distribuzione normale standard, \(Z \sim \mathcal{N}(0, 1)\). A partire da \(Z\) è possibile ottenere una famiglia di distribuzioni nel seguente modo
\[X = \mu + \sigma \cdot Z\]
con \(\mu, \sigma \in \mathbb{R}\). In questo caso diciamo che \(X\) è una v.a. con distribuzione normale di parametro \(\mu\) e \(\sigma^2\). In forma simbolica, \(X \sim \mathcal{N}(\mu, \sigma^2)\).
Il processo tramite il quale passiamo da una v.a. normale \(X \sim \mathcal{N}(\mu, \sigma^2)\) ad una v.a. normale standard \(Z \sim \mathcal{N}(0, 1)\), è molto spesso chiamato processo di normalizzazione, e viene effettuato nel seguente modo
\[Z = \frac{X - \mu}{\sigma}\]
In questo caso diciamo che \(Z\) è la "normalizzata" di \(X\). Notiamo che tramite la normalizzazione possiamo sempre ricondurre il calcolo della funzione di distribuzione di una v.a. normale qualsiasi a quello di una normale standard \(\Phi(\cdot)\), i cui valori sono ben noti già da tempo, e sono disponibili in tabelle della seguente forma
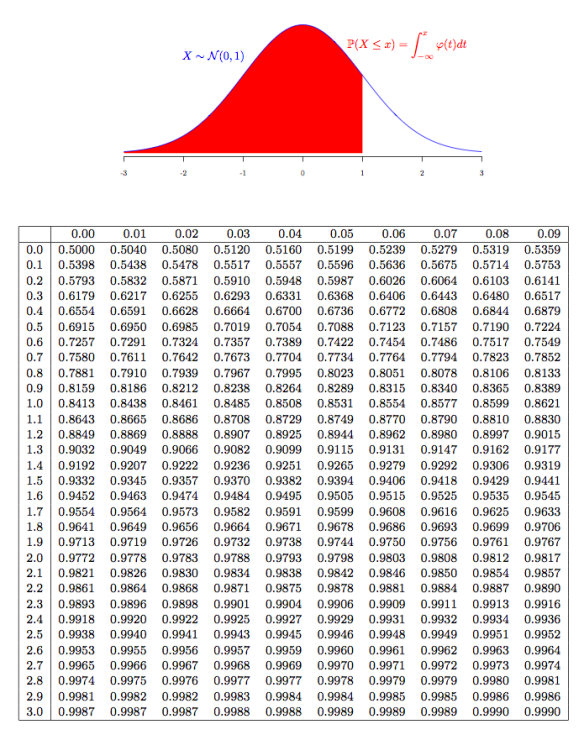
Ad esempio, se \(A \sim \mathcal{N}(175, 100)\), allora abbiamo che \[\begin{split} P(A \leq 180) &= P(\frac{A - 175}{10} \leq \frac{180 - 175}{10}) \\ &= P(Z \leq 0.5) \\ &= \Phi(0.5) \\ &= 0.6915 \\ \end{split}\]
4 Distribuzioni Multivariate
Se dobbiamo trattare più variabili aleatorie continue, ad esempio se abbiamo un vettore \((X_1, X_2, ..., X_k)\) di v.a. continue, si definisce la densità di tale vettore, chiamata la densità congiunta di \(X_1, X_2, ..., X_k\) come \(f(X_1, X_2, ..., X_k)\) che rispetta i seguenti vincoli
\(\int \int\limits_{\mathbb{R}^k} ... \int f(x_1, x_2, ..., x_k) \,\, dx_1 \,\, dx_2 \,\, ... \,\, dx_k = 1\)
\(f(x_1, x_2, ..., x_k) \geq 0\)
Questo significa che per calcolare la legge congiunta, ovvero per calcolare la probabilità \(P((X_1, X_2, ..., X_k) \in A\), con \(A \subseteq \mathbb{R}^k\), bisogna calcolare l'integrale multiplo con dominio di integrazione su \(A\).
4.1 Integrali Doppi
A questo punto può tornare utile ricordare come si calcolano gli integrali doppi. Supponiamo quindi di voler calcolare il seguente integrale doppio
\[\int_0^1 \int_0^1 x + y \,\, dy \, dx \]
Un integrale doppio ci permette di calcolare il volume dell'oggetto geometrico definito nello spazio tre dimensionale dalla funzione da integrare. Nel nostro particolare caso la funzione a due variabili è data da \(f(x, y) = x + y\), mentre il dominio di integrazione è il quadrato di lato \(1\) con un estremo nell'origine \((0,0)\) e un altro estremo nel punto \((1,1)\).
Al fine di calcolare un integrale doppio dobbiamo procede applicando lo stesso ragionamento utilizzato per il calcolo degli integrali singoli: Per calcolare il volume dell'oggetto in questione, spezziamo tale volume in tante superfici due dimensionali, calcoliamo l'area di ogni superficie e poi sommiamo tutte le aree calcolate per ottenere il volume finale. Formalmente il calcolo procedete nel seguente modo
\[\begin{split} \int_0^1 \int_0^1 x + y \,\, dy \, dx &= \int_0^1 [xy + y^2/2 \;\; \underset{y=0}{\overset{y=1}{|}} \;] dx \\ &= \int_0^1 x + 1/2 \,\, dx \\ &= [x^2/2 + 1/2x \;\; \underset{x=0}{\overset{x=1}{|}} \;] \\ &= 1/2 + 1/2 \\ &= 1 \\ \end{split}\]
Come altro esempio di calcolo di un integrale doppio, supponiamo di avere la seguente funzione a due variabili \(f(x, y)\), definita nel seguente modo
\[f(x, y) = \begin{cases} 1 &, \,\, x^2 + y^2 = 1 \\ 0 &, \,\, \text{ altrimenti } \\ \end{cases}\]
Vogliamo calcolare il volume dell'ogetto definito dalla funzione nel dominio dei punti \((x, y)\) in cui \(\{x^2 + y^2 = 1\}\). A tale fine spezziamo come prima il volume in tante superfici. Fissato \(x \in [-1, 1]\), \(y\) varia da \(-\sqrt{1 - x^2}\) a \(\sqrt{1 - x^2}\). Troviamo dunque il seguente integrale doppio
\[\begin{split} \overset{1}{\underset{x=-1}{\int}} \;\; \overset{\sqrt{1 - x^2}}{\underset{y=-\sqrt{1 - x^2}}{\int}} 1 \,\, dy \, dx &= \overset{1}{\underset{x=-1}{\int}} [ y \;\; \underset{y=-\sqrt{1-x^2}}{\overset{y=\sqrt{1 - x^2}}{|}} \;] \,\, dx \\ &= \overset{1}{\underset{x=-1}{\int}} \;\; 2\sqrt{1 - x^2} dx \\ &= \,\,... \\ &= 2\pi \\ \end{split}\]
4.2 Indipendenza con multiple v.a.
Ricordiamo che due v.a. continue \(X\) e \(Y\) si dicono indipendenti se e solo se
\[P((X \in A) \cap (Y \in B)) = P(X \in A) \cdot P(Y \in B), \,\, \forall A, B\]
Lavorando con v.a. indipendenti i calcoli si semplificano molto. Infatti, se \(X\) e \(Y\) sono indipendenti, allora la loro densità congiunta può essere spezzata nel seguente modo
\[f(x, y) = f_X(x) \cdot f_Y(y)\]
Questo ha delle conseguenze importanti nel calcolo degli integrali doppi. Infatti, se è possibile spezzare la densità congiuta, e se il dominio di integrazione è un prodotto cartesiano, allora il calcolo si semplifica enormemente, come è possibile vedere dal seguente esempio
\[\begin{split} P( (0 \leq X \leq 1) \cap (0 \leq Y \leq 1)) &= \int_0^1 \int_0^1 f(x,y) \, dy \, dx \\ &= \int_0^1 \int_0^1 f_x(x) \cdot f_y(y) \, dy \, dx \\ &= \int_0^1 f_x(x) \, dx \,\, \cdot \int_0^1 f_y(y) \, dy \\ \end{split}\]
per fare questo però richiediamo che \(X\) e \(Y\) siano due v.a. continue e indipendenti tra loro.
4.3 Densità Marginale e Densità Congiunta
Conoscendo la densità congiunta di un insieme di v.a. possiamo sempre ottenere la densità marginale di ciascuna v.a. presa in considerazione. Ad esempio, se abbiamo due v.a. \(X\) e \(Y\), e conosciamo la loro densità congiunta \(f(X, Y)\), per calcolare la densità marginale di \(X\) possiamo utilizzare la seguente formula
\[f_X(x) = \int\limits_{y = - \infty}^{\infty} f(x, y) \, dy\]
La funzione di distribuzione di \(X\) è quindi
\[F_X(t) = P(X \leq t) = \int_{-\infty}^t f_X(x) \, dx = \int_{-\infty}^t \int_{y = -\infty}^{\infty} f(x, y) \, dy \, dx\]
4.4 Valore Atteso, Varianza e Matrice di Covarianza
A seguire riportiamo come vengono calcolati i valori attesi e le varianze nel caso in cui trattiamo due v.a. \(X\) e \(Y\). Notiamo però che tutti questi risultati si possono facilmente generalizzare a \(n\) v.a. \(X_1\), \(X_2\), ..., \(X_n\).
\(\mathbb{E}[\begin{pmatrix} X \\ Y \\ \end{pmatrix}] = \begin{pmatrix} \mathbb{E}[X] \\ \mathbb{E}[Y] \end{pmatrix}\)
\(\mathbb{E}[g(X, Y)] = \int \int g(X, Y) \cdot f(X, Y) \, dx \, dy\)
\(Var[X + Y] = Var[X] + Var[Y] + 2 \cdot Cov[X, Y]\), con
\[Cov[X, Y] = \mathbb{E}[(X - \mathbb{E}[X]) \cdot (Y - \mathbb{E}[Y])]\]
Nel caso in cui \(X\) e \(Y\) sono indipendenti, il valore atteso e la varianza si semplificano nel seguente modo
\(\mathbb{E}[X \cdot Y] = \mathbb{E}[X] \cdot \mathbb{E}[Y]\)
\(Var[X + Y] = Var[X] + Var[Y]\), in quanto se \(X\) e \(Y\) sono indipendenti allora la loro covarianza è \(0\), \(Cov[X, Y] = 0\).
Al fine di descrivere la covarianza quando trattiamo con più v.a., si introduce la matrice di covarianza. Tale matrice contiene nella diagonale il valore della varianza per ogni v.a., e nel resto della matrice il valore della covarianza per ogni possibile coppia di v.a.
5 Trasformazione di Box-Muller
Siano \(X\) e \(Y\) due v.a. i.i.d. (indipendenti e identicamente distribuite) con distribuzione \(\mathcal{N}(0, 1)\). La trasformazione di Box-Muller è una tecnica che ci permette di simulare le v.a. \(X\) e \(Y\) utilizzando delle v.a. uniformi.
Consideriamo il piano cartesiano in cui possiamo mappare le nostre v.a. \(X\) e \(Y\), e andiamo ad eseguire la trasformazione in coordinate polari. Ad ogni punto \((x, y)\) del piano associamo due valori, \(r \geq 0\) e \(\theta\), che rappresentano rispettivamente l'ampiezza del vettore con coordinate \((x, y)\), e l'angolo, in radianti, tra l'asse delle \(x\) e il vettore con coordinate \((x, y)\). Troviamo quindi la seguente associazione
\[\begin{split} % TODO: what is theta exactly equal to? r &= \sqrt{x^2 + y^2} \;\; \longleftrightarrow \;\; x = r \cos{\theta} \\ \theta &\approx \arctan{\frac{y}{x}} \;\; \phantom{\longleftrightarrow} \;\;\;\;\;\, y = r \sin{\theta} \\ \end{split}\]
Poniamoci adesso il seguente quesito: come è cambiata la densità, ora che abbiamo effettuato questa trasformazione? Ricordiamo che, nel caso di una singola v.a., avevamo che se \(y = g(x)\), allora la densità di \(y\) è data da
\[f_y(y) = f_x(g^{-1}(y)) \cdot \frac{1}{g^{'}(g^{-1}(y))}\]
Tale formula può essere generalizzata tramite alcune modifiche e applicata al caso in cui abbiamo più v.a. In particolare, se ho un vettore di \(\bar{x} = \begin{pmatrix} x_1, x_2, ..., x_k \end{pmatrix}\) di \(k\) variabili aleatorie, e lo trasformo in un vettore \(\bar{u} = \begin{pmatrix} u_1, u_2, ... , u_k\end{pmatrix}\), con \(\bar{u} = \bar{g}(\bar{x})\) e in cui \(\bar{g}: \mathbb{R}^k \to \mathbb{R}^k\) è una funzione data da \(k\) funzioni \(g_1, g_2, ..., g_k\) con \(g_i: \mathbb{R}^k \to \mathbb{R}\) tale che \(u_i = g_i(x_1, x_2, ..., x_k)\), allora la densità di \(\bar{u}\) è data dalla seguente formula
\[f_{\bar{u}}(\bar{u}) = f_{\bar{x}}(g^{-1}(\bar{u})) \cdot \frac{d \bar{x}}{d \bar{u}}\]
dove con \(\frac{d \bar{x}}{d \bar{u}}\) intendiamo il determinante della matrice Jacobiana, che è la matrice \(J\) che contiene tutte le derivate parziali. In formula,
\[(J_{i, j}) = \frac{d x_i}{ d u_j}\]
Notiamo però che così facendo dobbiamo esprimere tutti i vari \(x_i\) in funzione dei vari \(u_j\). Per non dover fare questo, possiamo utilizzare la seguente uguaglianza
\[det(\frac{d \bar{x}}{d \bar{u}}) = \frac{1}{det(\frac{d \bar{u}}{d \bar{x}})}\]
Siamo quindi pronti ad applicare questa tecnica per simule due v.a. normali standard \(X\) e \(Y\). Come prima cosa consideriamo la loro densità congiunta. Dato che sono indipendneti, abbiamo che \(f(x, y) = f_x(x) \cdot f_y(y)\). E dato che sono entrambi \(\mathcal{N}(0, 1)\), troviamo la seguente densità congiunta, che viene anche chiamata cappello messicano
\[f(x, y) = \frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}} \cdot \frac{1}{\sqrt{2\pi}}e^{-\frac{y^2}{2}} = \frac{1}{2\pi} e^{-\frac{1}{2}(x^2+ y^2)}\]
Andando ad eseguire il cambio in coordinate polari \((r, \theta)\), ed esprimendo le vecchie coordinate \((x, y)\) nelle nuove, troviamo che
\[x = r \cos{\theta} \;\;\;,\;\;\; y = r \sin{\theta}\]
Inoltre, il determinante del Jacobiano è dato da
\[\frac{d \bar{x}}{d \bar{\theta}} = \begin{vmatrix} \dfrac{d x}{d r} & \dfrac{d x}{d \theta} \\[2ex] \dfrac{d y}{d r} & \dfrac{d y}{d \theta} \\[2ex]\end{vmatrix} = \begin{vmatrix} \cos{\theta} & -r\sin{\theta} \\[2ex] \sin{\theta} & r\cos{\theta} \\[2ex] \end{vmatrix} = rcos^2{\theta} + rsin^2{\theta} = r \]
Utilizzando le formule descritte in precedenza troviamo che la densità congiunta delle due v.a. normali standard in coordinate polari è data da
\[f(r, \theta) = \frac{1}{2\pi}e^{-\frac{1}{2}r^2} \cdot r\]
Notiamo che con questa trasformazione abbiamo spostato lo spazio della densità da \(\mathbb{R}^2\) al rettangolo infinito dato dai punti contenuti in \(\mathbb{R} \times [0, 2\pi]\). In particolare poi notiamo come siamo riusciti ad esprimere la densità come un prodotto di densità. Infatti \(\frac{1}{2\pi}\) è la densità di una uniforme nell'intervallo \([0, 2\pi]\), mentre \(e^{-\frac{r^2}{2}} \cdot r\) è una densità per \(r\) in \(\mathbb{R}\) in quanto
\[\int_0^{\infty}e^{-\frac{r^2}{2}} \cdot r \, dr = -e^{-\frac{r^2}{2}} \;\; \underset{0}{\overset{\infty}{|}} \; = 1\]
Osservazione: In generale, se riesco ad esprimere una densità congiunta come prodotto di densità marginali, allora posso essere sicuro che le v.a. in questione sono indipendenti.
Come ultima cosa, notiamo che
\[\begin{split} P[r^2 \leq t] &= P[r \leq \sqrt{t}] \\ &= \int_0^{\sqrt{t}} r e^{-\frac{r^2}{2}} \; dr \\ &= 1 - e^{-t/2} \\ &= F_Z(1/2) \end{split}\]
con \(Z \sim Exp(1/2)\). Detto altrimenti, abbiamo che \(r^2 \sim Exp(1/2)\).
Adesso abbiamo tutto quello che ci serve per descrivere il modo in cui simulare le v.a. \(X\) e \(Y\). Il metodo è descritto come segue
Prendiamo due uniformi \(U_1, U_2 \sim U[0, 1]\).
Calcoliamo \(U_1 \cdot 2\pi \sim \theta\).
Calcoliamo \(-\ln(U_2) \cdot 2 \sim Exp(1/2)\).
Calcoliamo \(\sqrt{-\ln(U_2)\cdot 2} \sim r\).
Utilizzando \((r, \theta)\) mi calcolo \(x\) e \(y\) come segue
\[x = r \cos{\theta} \,\, , \,\, y = r \sin{\theta}\]
6 Linguaggio R
Il linguaggio \(R\) è un linguaggio di programmazione che, tra le altre cose, permette di gestire varie quantità correllate con alcune delle più importanti distribuzioni conosciute in statistica. Ad esempio, abbiamo le seguenti funzioni correlate con la distribuzione normale standard:
pnorm(\(\cdot\)): permette di calcolare la funzione di ripartizione, ovvero in questo caso la funzione \(\Phi(\cdot)\).
qnorm(\(0.975\)), che permette di calcolare il punto della retta dei reali in cui dobbiamo andare per avere una probabilità di \(0.975\).
dnorm(\(\cdot\)), che permette di calcolare la funzione di densità, in questo caso la funzione \(\phi(\cdot)\).
rnom(\(k\)), che genera un vettore con \(k\) numeri generati dalla distribuzione \(\mathcal{N}(0,1)\).