ISTI - 05 - Statistiche D'ordine
1 Informazioni Lezione
Data:
In questa lezione abbiamo introdotto la funzione di ripartizione empirica e le statistiche d'ordine.
2 Funzione di Ripartizione Empirica
In statistica, quando lavoriamo con un campione di dati \(X_1, ..., X_n\) i.i.d., possiamo avere due approcci diversi:
Possiamo assumere il tipo di distribuzione che ha generato i dati su cui vogliamo lavorare. Ad esempio, possiamo assumere che i dati provengano da una distribuzione normale con media \(\mu\) e varianza \(\sigma^2\), ovvero che \(X_i \sim \mathcal{N}(\mu, \sigma^2)\). In questo caso ci poniamo il problema di stimare i valori dei parametri della distribuzione, e il problema da risolvere diventa un problema parametrico.
Altre volte invece non vogliamo assumere niente sul tipo di distribuzione prima di inferire qualcosa sulla distribuzione. In questo caso il problema da risolvere è un problema non-parametrico.
Poniamoci adesso nel secondo caso. Sia \(X\) i.i.d. al campione da noi analizzato, e supponiamo di voler dire qualcosa su \(F_X(t) := P(X \leq t)\). A tale fine introduciamo la funzione di ripartizione empirica, definita come segue
\[\hat{F}_n(t) := \frac{1}{n} \cdot \#\{X_i \leq t\}\]
Notiamo che la v.a. che conta il numero dei \(X_i\) che sono minori di \(t\) è una v.a. con distribuzione binomiale di parametri \(Bin(n, F(t))\). Per le caratteristiche della distribuzione binomiale poi, la funzione di ripartizione empirica rappresenta uno stimatore consistente della vera funzione di ripartizione. Valgono infatti le seguenti cose
La media di \(\hat{F}_n(t)\) è proprio \(F(t)\).
\[\mathbb{E}[\hat{F}_n(t)] = \frac{1}{n} \cdot \mathbb{E}[Bin(n, F(t))] = \frac{1}{n} \cdot n \cdot F(t) = F(t)\]
La varianza di \(\hat{F}_n(t)\) tende a \(0\) al crescere di \(n\).
\[Var[\hat{F}_n(t)] = \frac{1}{n^2} \cdot Var[Bin(n, F(t))] = \frac{nF(t)(1 - F(t))}{n^2} = \frac{F(t)(1 - F(t))}{n}\]
Così facendo, fissato \(t\) possiamo utilizzare \(\hat{F}_n(t)\) per stimare il valore di \(F(t)\). Se vogliamo invece studiare \(\hat{F}_n(t)\) come funzione di \(t\), dobbiamo ordinare i vari campioni \(X_1, X_2, ..., X_n\) in una statistica d'ordine \(X_{(1)}, X_{(2)}, ..., X_{(n)}\) con \(X_{(i)} \leq X_{(i+1)}\) in modo tale da ottenere il seguente grafico
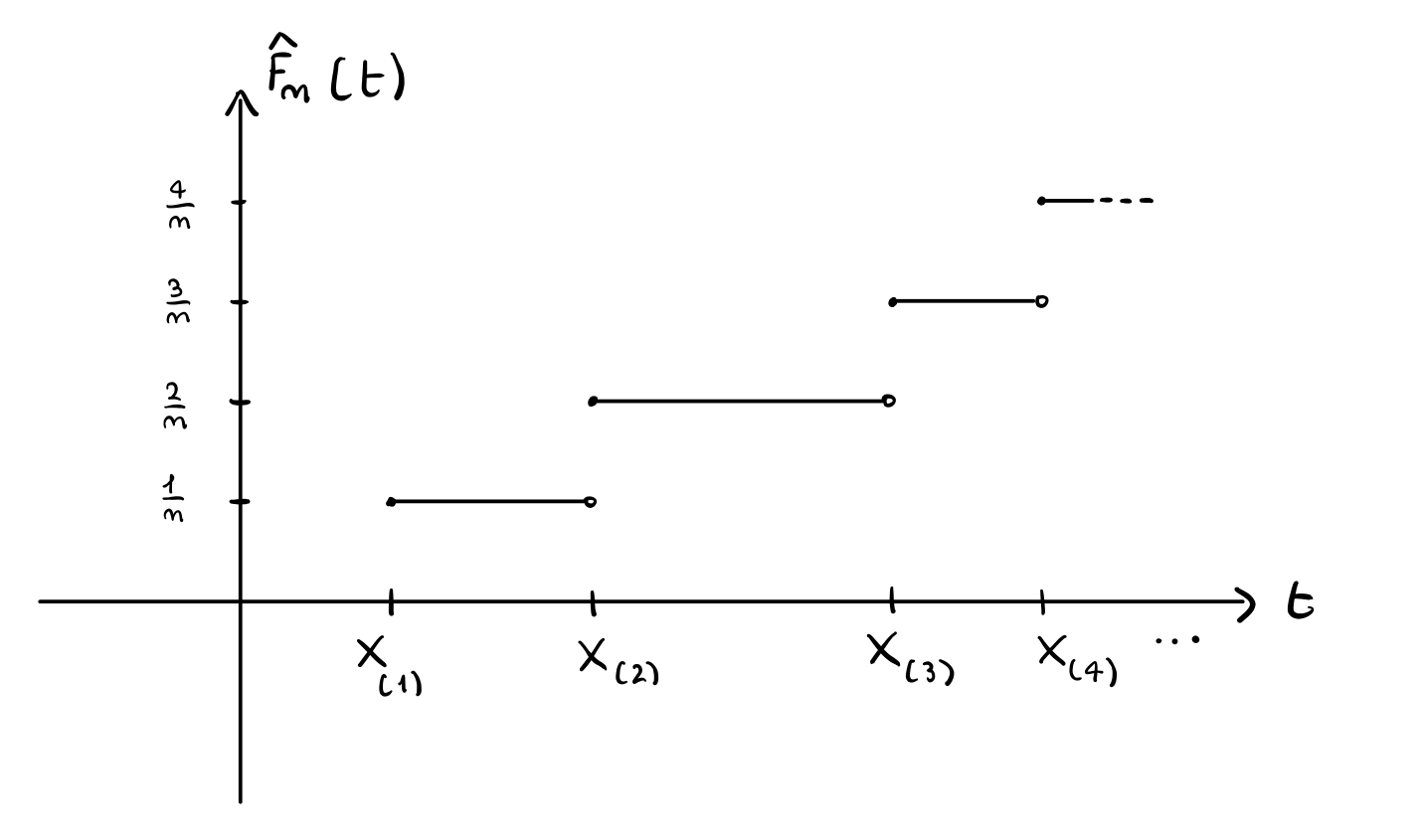
3 Statistiche D'ordine
Dato un campione \(X_1, X_2, ..., X_n\) i.i.d. si indica con \(X_{(1)}, X_{(2)}, ..., X_{(n)}\) il suo riordinamento, ovvero la sequenza di v.a. tale che \(X_{(1)} \leq X_{(2)} \leq ... \leq X_{(n)}\). Tale vettore prende il nome di statistica d'ordine, mentre \(X_{(k)}\) è una funzione dei valori campionari, e viene chiamata la k-esima statistica d'ordine del vettore \(X_1, X_2, ..., X_n\).
Andiamo adesso ad analizzare la distribuzione di alcune di queste statistiche d'ordine.
3.1 Distribuzione del massimo \(X_{(n)}\)
Per analizzare la distribuzione del massimo ci basta osservare la seguente equivalenza tra eventi: dire che il massimo di un insieme di valori è minore di \(t\) equivale a dire che tutti i valori sono minori di \(t\). Utilizzando poi l'indipendenza e il fatto che condividono tutte la stessa distribuzione, troviamo il seguente risultato per la funzione di ripartizione del massimo
\[\begin{split} F_{X_{(n)}}(t) = P(X_{(n)} \leq t) &= P(X_{1} \leq t, \,\, X_{2} \leq t, \,\,...,\,\, X_{n} \leq t) \\ &= \prod_{i = 1}^n P(X_{i} \leq t) \\ &= (F(t))^n \end{split}\]
la densità del massimo è invece data da
\[f_{X_{(n)}} = n(F(t))^{n-1} \cdot f(t)\]
3.2 Distribuzione del minimo \(X_{(1)}\)
Per quanto riguarda la distribuzione del minimo, notiamo che è più conveniente calcolare la funzione di sopravvivenza, ovvero l'evento complementare a \((X_{(1)} \leq t)\). In questo caso la seguente espressione per la funzione di ripartizione del minimo
\[\begin{split} P(X_{(1)} \leq t) &= 1 - P(X_{(1)} > t) \\ &= 1 - P(X_{1} > t, \,\, X_2 > t, \,\, ..., \,\, X_n > t) \\ &= 1 - (1 - F(t))^n \end{split}\]
la densità del minimi è invece data da
\[f_{X_{(1)}}(t) = n(1 - F(t))^{n-1} \cdot f(t)\]
3.3 Distribuzione del \(k-\) esimo \(X_{(k)}\)
Per quanto riguarda il calcolo della distribuzione della $k-$esima statistica d'ordine, sono possibili due approcci, il primo logico e formale e il secondo più intuitivo e informale.
Iniziamo con quello logico e formale. Questo approccio consiste in una generalizzazione del metodo usato precedentemente per il calcolo della distribuzione del massimo di una statistica d'ordine. L'approccio si basa infatti sulla seguente equivalenza tra eventi
\[X_{(k)} \leq t \iff \text{almeno } k \leq t\]
Per semplicità nei calcoli definiamo \(N := \#\{X_i \leq t\}\). Troviamo dunque
\[\begin{split} P(X_{(k)} \leq t) &= P(\text{ almeno } k \leq t) \\ &= \sum_{i = k}^n P(N = i) \\ &= \sum_{i = k}^n \binom{n}{i} F(t)^i (1 - F(t))^{n - i} \end{split}\]
3.4 Esempio: Massimo di \(n\) Uniformi
Siano \(X_1, X_2, ..., X_n \sim U[0, 1]\) e supponiamo di voler calcolare la distribuzione di \(X := \max_i X_i\). Utilizzando le formule viste prime troviamo
\[P(X \leq t) = P(\max X_i \leq t) = F(t)^n = t^n \]
e quindi \(f_X(t) = nt^{n-1}\). Da questo segue che la media di \(X\) è pari a
\[\mathbb{E}[X] = \int_{0}^1 t \cdot f_X(t) dt = \int_0^t n \cdot t^n dt = \frac{n}{n+1}\]
tale risultato è intuitivamente sensato, in quanto ci dice che il massimo di \(n\) uniformi in \([0, 1]\), in media, è molto vicino al valore \(1\).