ISTI - Coordinate Polari
1 Introduzione
In questo documento è presente una breve trattazioni su come è possibile utilizzare le coordinate polari nella risoluzione di integrali doppi. Questa tecnica viene molto spesso utilizzata nel calcolo della distribuzione di una qualche funzione di variabili aleatorie.
2 Coordinate Cartesiane e Coordinate Polari
Ricordiamo che utilizzando le coordinate cartesiane i punti del piano vengono espressi da una coppia di numeri \(P = (x_0, y_0)\), dove
- \(x_0\) rappresenta la distanza che la proiezione ortogonale del punto \(P\) sull'asse delle ascisse ha rispetto all'origine.
- \(y_0\) rappresenta la distanza che la proiezione ortogonale del punto \(P\) sull'asse delle ordinate.
Graficamente troviamo,
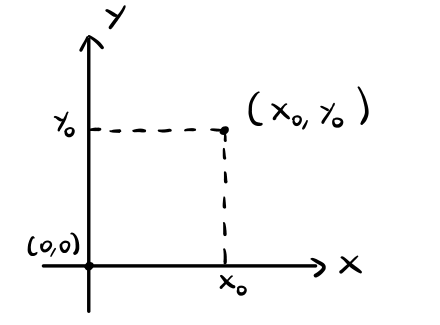
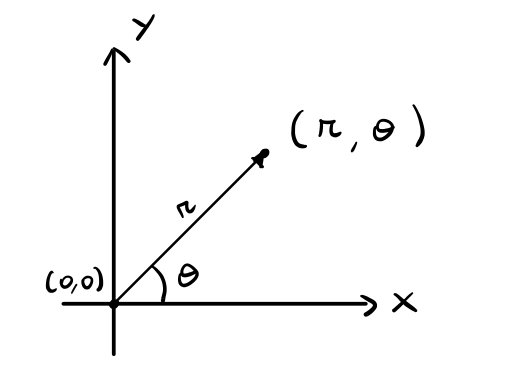
Utilizzando invece le coordiante polari, i punti del piano vengono espressi da una coppia di numeri \(P' = (r, \theta)\), dove
- \(r\) rappresenta la distanza dall'origine del punto in questione.
- \(\theta\) rappresenta l'angolo che il punto forma con l'asse orizzontale.
Graficamente troviamo,
3 Esprimere un Integrale Doppio in Coordinate Polari
Consideriamo adesso il seguente integrale doppio, inizialmente espresso nelle tradizionali coordinate cartesiane
\[\iint\limits_D f(x, y) \,\, dy \,dx\]
dove \(D \subseteq \mathbb{R}^2\) è il dominio di integrazione.
Per esprimere tale integrale utilizzando le coordinate polari dobbiamo effettuare i seguenti steps:
- Esprimere la funzione \(f(x, y)\) in funzione di \(r\) e \(\theta\).
Questo passo può essere fatto utilizzando le seguenti equazioni di conversione
\[\begin{cases} x = r \cos{\theta} \\ y = r \sin{\theta} \\ \end{cases}\]
Una identità molto utile per effettuare questo passo deriva da queste equazioni equazioni, ed è la seguente
\[x^2 + y^2 = (r \cos{\theta})^2 + (r \sin{\theta})^2 = r^2 \cdot (\cos^2{\theta} + \sin^2{\theta}) = r^2 \cdot 1 = r^2\]
- Esprimere \(dx \, dy\) in funzione di \(dr\) e \(d\theta\).
Questo passo non dipende dalla particolare funzione da integrare o dal particolare dominio di integrazione. È Infatti possibile dimostrare che passando dalle coordinate cartesiane a quelle polari si ha la seguente trasformazione
\[dy \, dx \longrightarrow r \cdot \, dr \, d\theta\]
- Esprimere il domindio \(D\) in funzione di \(r\) e \(\theta\).
Per fare questo passo dobbiamo capire come variano \(r\), ovvero la distanza dei punti in \(D\) dall'origine, e \(\theta\), ovvero l'angolo che i punti di \(D\) formano con l'asse delle ascisse.
4 Esempi
Andiamo adesso a presentare qualche esempio di calcolo di un integrale doppio tramite una conversione in coordinate polari.
4.1 Esempio 1
Consideriamo il seguente integrale doppio
\[\iint\limits_D e^{-(x^2 + y^2)} \,\, dy\,dx \,\,\,\, , \,\,\,\, D = \{(x, y) \in \mathbb{R}^2: \,\, x = \sqrt{4 - y^2}\}\]
Procediamo quindi con i vari steps come descritti in precedenza:
- Per esprimere \(f(x, y) = e^{-(x^2 + y^2)}\) in funzione di \(r\) e
\(\theta\) utilizziamo l'identità dimostrata in precedenza per
ottenere la seguente espressione
\[e^{-(x^2 + y^2)} = e^{-r^2}\]
- Per esprimere \(dx\) e \(dy\) in funzione di \(dr\) e \(d\theta\)
utilizziamo la trasformazione standard
\[dy \, dx \longrightarrow r \cdot \, dr \, d\theta\]
- Infine, per rappresentare il dominio \(D\) in funzione di \(r\) e
\(\theta\) una cosa molto utile da fare è rappresentarlo. Nel
nostro caso troviamo il seguente dominio di integrazione
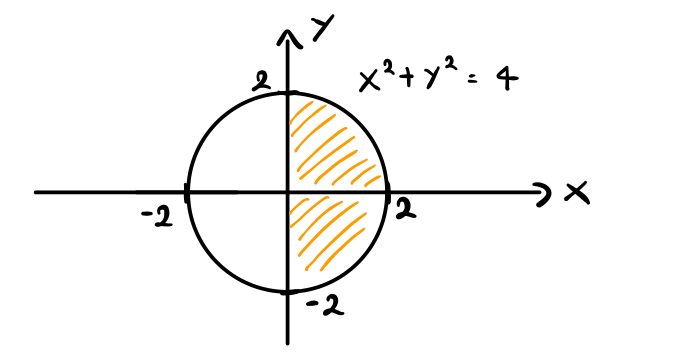
dalla figura possiamo notare che tutti i punti nel dominio \(D\) si trovano ad una distanza dall'origine compresa tra \(0\) e \(2\). Ma allora il valore di \(r\) in \(D\) varia da \(0\) e \(2\), e quindi \(r \in [0, 2]\). Per quanto riguarda il valore di \(\theta\), abbiamo che esso varia da \(-\pi/2\) a \(\pi/2\), e quindi \(\theta \in [-\pi/2, \pi/2]\).
Mettendo tutto assieme otteniamo la seguente trasformazione
\[\underbrace{\iint\limits_D e^{-(x^2 + y^2)} \,\, dy \, dx}_{\text{coordinate cartesiane}} \,\, = \,\, \underbrace{\int\limits_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \int\limits_0^2 e^{-r^2} \cdot r \,\, dr \, d\theta}_{\text{coordinate polari}}\]
Notiamo che adesso l'integrale è diventato molto più semplice da calcolare. Troviamo infatti il seguente risultato
\[\begin{split} \int\limits_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \int\limits_0^2 e^{-r^2} \cdot r \,\, dr \, d\theta \,\, &= \int\limits_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \Big[ -\frac{e^{-r^2}}{2} \;\; \underset{r=0}{\overset{r=2}{|}} \;\Big]\\ &= \int\limits_{-\frac{\pi}{2}}^{\frac{\pi}{2}} -\frac{e^{-4}}{2} + \frac12 \,\, d\theta \\ &= \Big[ -\frac{e^{-4}}{2} \cdot \theta + \frac12 \cdot \theta \;\; \underset{\theta=-\frac{\pi}{2}}{\overset{\theta=\frac{\pi}{2}}{|}} \Big] \\ &= -\frac{e^{-4}}{2} \cdot \frac{\pi}{2} + \frac12 \cdot \frac{\pi}{2} - \Big(\frac{e^{-4}}{2} \cdot \frac{\pi}{2} - \frac12 \cdot \frac{\pi}{2}\Big) \\ &= -e^{-4} \cdot \frac{\pi}{2} + \frac{\pi}{2} \\ &= \frac{\pi}{2} \cdot \Big(1 - e^{-4}\Big) \\ \end{split}\]
Riassumendo, abbiamo trovato che
\[\iint\limits_D e^{-(x^2 + y^2)} \,\, dy\,dx = \frac{\pi}{2} \cdot \Big(1 - e^{-4}\Big)\]
per concludere questo esempio, notiamo che dal punto di vista geometrico abbiamo effettuato la seguente trasformazione dello spazio
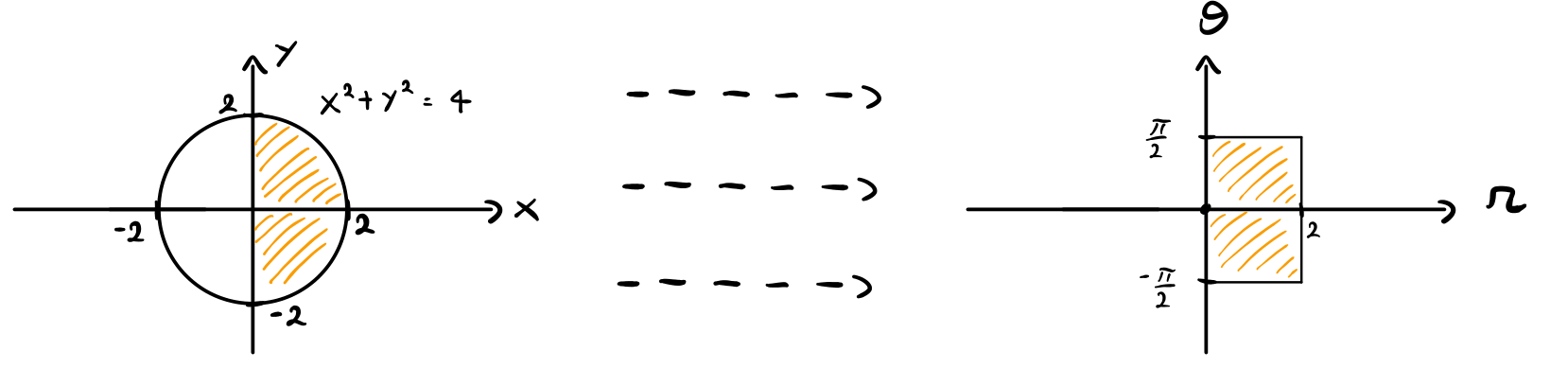
4.2 Esempio 2
Consideriamo il seguente integrale doppio
\[\iint\limits_D \frac{1}{2\pi} e^{-\frac12 \cdot (x^2 + y^2)} \,\, dy\,dx \,\,\,\, , \,\,\,\, D = \{(x, y) \in \mathbb{R}^2: y \geq -x \}\]
Procediamo quindi eseguendo i soliti passi per esprimere il nostro integrale in coordinate polari:
- La funzione da integrare \(f(x, y)\) viene espressa nel seguente
modo
\[\frac{1}{2\pi} e^{-\frac12 \cdot (x^2 + y^2)} = \frac{1}{2\pi} e^{-\frac12 \cdot r^2}\]
- Per quanto riguarda il dominio \(D\) invece, rappresentandolo
troviamo la seguente figura
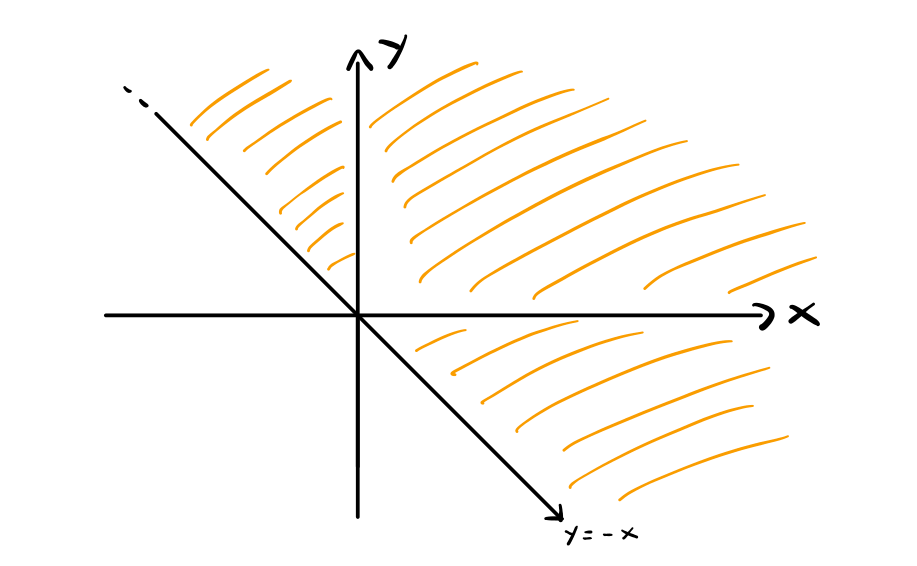
troviamo quindi che \(r \in [0, +\infty)\) e \(\theta \in [-\frac{\pi}{4}, \frac{3\pi}{4}]\).
Mettendo tutto assieme otteniamo
\[\begin{split} \iint\limits_D \frac{1}{2\pi} e^{-\frac12 \cdot (x^2 + y^2)} \,\, dy\,dx &= \int\limits_{-\frac{\pi}{4}}^{\frac{3\pi}{4}} \int\limits_0^{\infty} \frac{1}{2\pi} e^{-\frac12 r^2} r \, dr d\theta \\ &= \int\limits_{-\frac{\pi}{4}}^{\frac{3\pi}{4}} \frac{1}{2\pi} \cdot 1 \, dr d\theta \\ &= \frac{1}{2\pi} \cdot \big(\frac{3\pi}{4} + \frac{\pi}{4} \big) \\ &= \frac12 \\ \end{split}\]