ML - 02 - Fitting of Polynomial I
Date:
Lecturer: Giorgio Gambosi
Slides:
Table of contents:
In questa lezione abbiamo affrontato il nostro primo problema di machine learning.
Continuiamo la nostra introduzione al mondo del machine learning considerando un problema di inferenza sufficientemente semplice da poter essere trattato immediatamente ma anche sufficientemente complesso da poter discutere di una serie di considerazioni riguardanti ml nel contesto dell'apprendimento supervisionato.
Il problema che vogliamo affrontare è noto con il nome fitting of polynomials, ed è così descritto: abbiamo una funzione \(f(\cdot): \mathbb{R} \to \mathbb{R}\) ad una sola variabile e abbiamo \(n\) osservazioni \((x_1, t_1), \ldots, (x_n, t_n)\), dove \(f(x_i) = t_i\) per ogni \(i\). Il nostro obiettivo è quello di utilizzare queste osservazioni per inferire, per un qualunque valore \(\tilde{x} \in \mathbb{R}\) (dunque anche un valore diverso dagli \(x_i\)), il corrispondente valore del target \(t\).
Possiamo immaginare il nostro training set come una coppia di vettori
\[\begin{split} \textbf{x} &= \begin{pmatrix} x_1 & x_2 & \ldots & x_n \end{pmatrix}^T \\ \textbf{t} &= \begin{pmatrix} t_1 & t_2 & \ldots & t_n \end{pmatrix}^T \\ \end{split}\]
che sono relazionatori tra loro tramite una relazione funzionale a noi sconosciuta.
Supponiamo di avere il seguente training set.
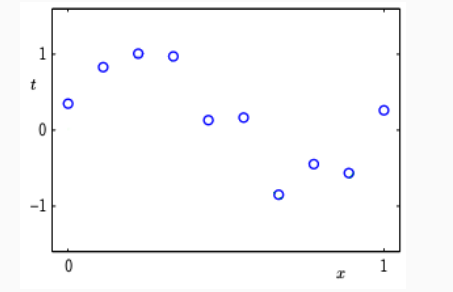
e supponiamo che il training set sia stato generato partendo dalla funzione funzione \(f(x) = t = \sin(2 \pi x)\) a cui poi si aggiunge un rumore gaussiano con media \(0\) e varianza \(\sigma^2\). Dunque abbiamo che
\[t_i = f(x_i) + \epsilon_i = \sin(2 \pi x_i) + \epsilon_i\]
con \(\epsilon_i \sim \mathcal{N}(0, \sigma^2)\).
Possiamo visualizzare la nostra funzione originaria nel seguente grafo, che è rappresentata dalla curva verde.
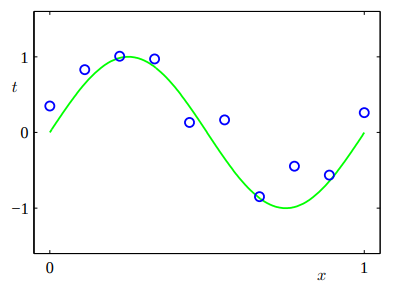
Mettiamoci ora nei panni di qualcuno che non conosce questa relazione e che invece la vuole approssimare utilizzando le osservazioni note, che contengono un piccolo errore derivante dal fattore \(\epsilon_i\).
Tra tutte le funzioni possibili che ci permettono di approssimare la nostra funzione \(f(\cdot)\) andiamo a restringere il campo di ricerca alle sole funzioni polinomiali. In particolare quindi supponiamo di utilizzare come modello un polinomio di grado \(M > 0\)
\[y(y, \textbf{w}) = w_0 + w_1 x + w_2 x^2 + \ldots + w_M x^M = \sum\limits_{j = 0}^M w_j x^j\]
Il nostro obiettivo sarà quindi quello di calcolare i coefficienti del polinomio, ovvero il vettore
\[\textbf{w} = \begin{pmatrix} w_1 & w_2 & \ldots & w_M \end{pmatrix}^T\]
Da notare che la funzione che noi andiamo a considerare è una funzione di grado \(M\) rispetto alla \(x\), ma è una funzione lineare rispetto al vettore \(\textbf{w}\). Dato che dal nostro punto di vista le incognite non sono le potenze delle \(x\) ma i pesi \(w_i\), abbiamo che il modello che vogliamo è un modello lineare rispetto a \(\textbf{w}\).
A questo punto il nostro problema diventa quello di trovare il vettore dei pesi \(\textbf{w}\) che mi fornisce il polinomio che si comporta "meglio", dove ovviamente il significato di "meglio" deve essere definito.
In generale però nel contesto del machine learning con "meglio" si intende il fatto che \(\textbf{w}\) definisce un polinomio che minimizza una determinata error function (o cost function) quando viene applicato ai dati del training set.
Uno dei metodi più tradizionali per valutare la qualità dell'approssimazione fornita da un determinato polinomio è la somma dei quadrati delle differenze. Questa funzione di errore è nota sotto il nome di least squares ed è definita nel seguente modo
\[\begin{split} E(\textbf{w}) &= \frac12 \sum\limits_{i = 1}^n (y(x_i, \textbf{w}) - t_i)^2 \\ &= \frac12 \sum\limits_{i = 1}^n \Big(w_0 + w_1 x_i + w_2 x_i^2 + \ldots + w_M x_i^M - t_i \Big)^2 \\ \end{split}\]
come è possibile vedere, la funzione si calcola tramite la differenza, al quadrato, tra il valore ritornato dal nostro modello e il valore del target fornitoci dal training set.
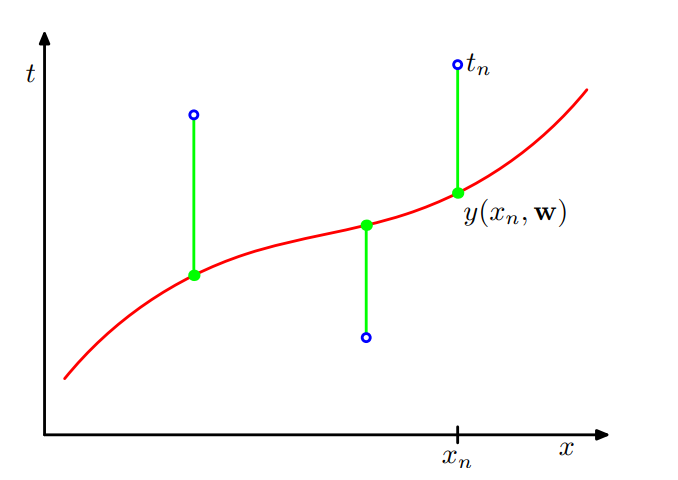
Il nostro obiettivo diventa quindi quello di trovare il vettore dei pesi che minimizza tale funzione.
Idealmente vorremmo trovare il valore \(\textbf{w}\) che minimizza in modo assoluto la funzione \(E(\textbf{w})\). Detto questo, trovare il minimo assoluto è un problema molto difficile, e dunque ci accontentiamo di trovare i vettori \(\textbf{w}\) che azzerano la derivata di \(E(w)\) rispetto a \(\textbf{w}\). Notiamo poi che in questo caso c'è un solo punto di minimo, in quanto \(E(\textbf{w})\) è una funzione quadratica, e quindi la sua derivata è lineare, ovvero si azzera in un punto solo, da adesso in poi denotato con \(\textbf{w}^*\).
Dato che \(\textbf{w}\) è un vettore, la derivata rispetto a \(\textbf{w}\) è in realtà una collezione di derivate. Azzerandole tutte otteniamo il seguente sistema lineare
\[\begin{cases} \frac{\partial E(\textbf{w})}{\partial w_0} &= \,\, \sum\limits_{i = 1}^n (y(x_i, \textbf{w}) - t_i) = 0 \\ \frac{\partial E(\textbf{w})}{\partial w_1} &= \,\, \sum\limits_{i = 1}^n x_i (y(x_i, \textbf{w}) - t_i) = 0 \\ &\vdots \\ \frac{\partial E(\textbf{w})}{\partial w_M} &= \,\, \sum\limits_{i = 1}^n x_i^M (y(x_i, \textbf{w}) - t_i) = 0 \\ \end{cases}\]
in quanto, ad esempio
\[\begin{split} \frac{\partial E(\textbf{w})}{\partial w_0} &= \frac{\partial }{\partial w_0} \Big[ \frac12 \cdot \sum\limits_{i = 1}^n \Big(w_0 + w_1 x_i + w_2 x_i^2 + \ldots + w_M x_i^M - t_i \Big)^2 \Big] \\ &= \frac12 \cdot \frac{\partial }{\partial w_0} \Big[ \sum\limits_{i = 1}^n \Big(w_0 + w_1 x_i + w_2 x_i^2 + \ldots + w_M x_i^M - t_i \Big)^2 \Big] \\ &= \frac12 \Big[\sum\limits_{i = 1}^n \frac{\partial }{\partial w_0} \Big(w_0 + w_1 x_i + w_2 x_i^2 + \ldots + w_M x_i^M - t_i \Big)^2 \Big] \\ &= \frac12 \Big[\sum\limits_{i = 1}^n 2 \cdot \Big(w_0 + w_1 x_i + w_2 x_i^2 + \ldots + w_M x_i^M - t_i \Big) \\ &\;\;\;\;\;\;\;\;\;\;\;\;\; \cdot \frac{\partial }{\partial w_0} \Big(w_0 + w_1 x_i + w_2 x_i^2 + \ldots + w_M x_i^M - t_i \Big) \Big] \\ &= \frac12 \cdot 2 \cdot \Big[\sum\limits_{i = 1}^n \Big(w_0 + w_1 x_i + w_2 x_i^2 + \ldots + w_M x_i^M - t_i \Big) \cdot 1 \Big] \\ &= \sum\limits_{i = 1}^n \Big(w_0 + w_1 x_i + w_2 x_i^2 + \ldots + w_M x_i^M - t_i \Big) \\ &= \sum\limits_{i = 1}^n (y(x_i, \textbf{w}) - t_i) \\ \end{split}\]
Notiamo che il sistema trovato è un sistema linare di \(M+1\) equazioni in \(M+1\) incognite, e quindi, a meno di casi degenere, ammette una e una sola soluzione.
La soluzione che troviamo risolvendo questo sistema lineare è il vettore \(\mathbf{w}^*\) che minimizza la funzione di errore richiesta. Dunque alla fine il modello calcolato risulta essere \(y(x, \mathbf{w}^*)\).
Notiamo che prima ancora di arrivare al punto in cui abbiamo trovato il giusto vettore dei pesi \(\mathbf{w}^*\), abbiamo prima scelto il particolare grado del polinomio che volevamo utilizzare come modello. In altre parole quindi c'è un ulteriore parametro, un iper-parametro, che entra in gioco prima ancora di trovare i parametri del modello. Il valore di questo iper-parametro determina il particolare modello e i particolari sotto-parametri che dobbiamo stimare.
Nel nostro caso l'iper-parametro è il grado \(M\) del polinomio che vogliamo utilizzare come modello. Ragionare su quale grado scegliere è un esempio di model selection, in quanto il valore di \(M\) determina il particolare modello che vogliamo utilizzare e quindi il numero di parametri del vettore \(\mathbf{w}\) da stimare. Mentre una volta fissato il valore di \(M\) per determinare il miglior vettore \(\mathbf{w}^*\) possiamo procedere come discusso prima, per scegliere invece qual è il migliore valore di \(M\) dobbiamo trovare qualche altro modo.
È possibile vedere che più aumento il parametro \(M\) e più sarò in grado di approssimare l'insieme dei punti che forma il mio training set.
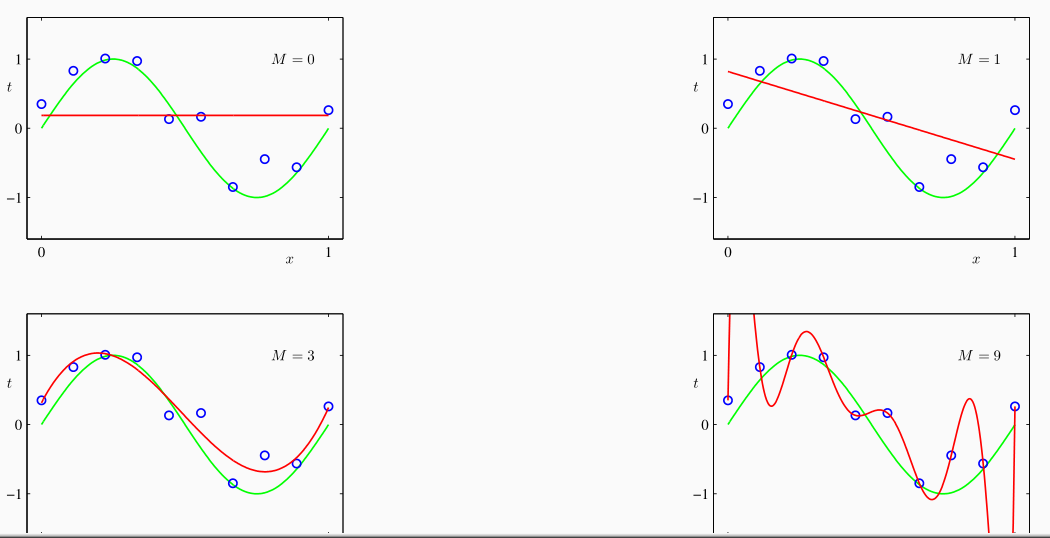
Al limite, se \(M + 1 = n\), il modello permette di ottenere un errore nullo, ovvero si ha che \(y(x_i, \mathbf{w}^*) = t_i\) per \(i = 1, \ldots n\). Osserviamo però che avere un errore nullo non è poi un risultato così gradevole, in quanto il nostro obiettivo non è stimare il valore dei punti già presenti nel training set, ma è bensì riuscire a generalizzare dall'esperienza per approssimare il valore dei punti che non fanno parte del training set. Questo fenomeno è chiamato overfitting.
Granted, a model thats too simple can fail to capture the essential pattern of the data. On the other hand, a model thats too complicated becomes oversensitive to the particular data points that we happened to observe. As a consequence, precisely because it is tuned so finely to that specific data set, the solutions it produces are highly variable. [...] So one of the deepest truths of machine learning is that, in fact, its not always better to use a more complex model, one that takes a greater number of factors into account. And the issue is not just that the extra factors might offer diminishing returns, performing better than a simpler model, but not enough to justify the added complexity. Rather, they might make our predictions dramatically worse.
Algorithms to Live by, Brian Christian, Thomas L. Griffiths.
Per andare a vedere come si comporta il nostro modello assumiamo di avere un ulteriore insieme di osservazioni denotato \(X_{\text{test}}\) e chiamato test set, che contiene \(100\) ulteriori osservazioni generate sempre nello stesso modo di prima.
L'idea è quella di separare il test set dal training set, utilizzare i dati contenuti nel training set per costruire il nostro modello, e utilizzare i dati contenuti nel test set per valutare il modello costruito.
In particolare, fissato un coefficiente \(M\):
Come prima cosa deriviamo il vettore \(\mathbf{w}^*\) dal training set \(X_{\text{traing}}\).
Successivamente calcoliamo l'errore sul test set, ovvero calcoliamo
\[E(\mathbf{w}^*, X_{\text{test}})\]
In alternativa possiamo calcolare la radice quadrata dell'errore medio empirico, ovvero
\[\begin{split} E_{\text{RMS}}(\mathbf{w}^*, X_{\text{test}}) &= \sqrt{\frac{E(\mathbf{w}^*, X_{\text{test}})}{|X_{\text{test}}|}} \\ &= \sqrt{\frac{1}{2 |X_{\text{test}}|} \sum\limits_{x \in X_{\text{test}}} \Big(y(x, \mathbf{w}) - t\Big)^2} \end{split}\]
Un valore basso di \(E_{\text{RMS}}(\mathbf{w}^*, X_{\text{test}})\), dove RMS sta per Root Mean Square è un segno di una buona generalizzazione.
Se andiamo a plottare l'errore \(E_{\text{RMS}}\) rispetto al valore \(M\) otteniamo il seguente grafico
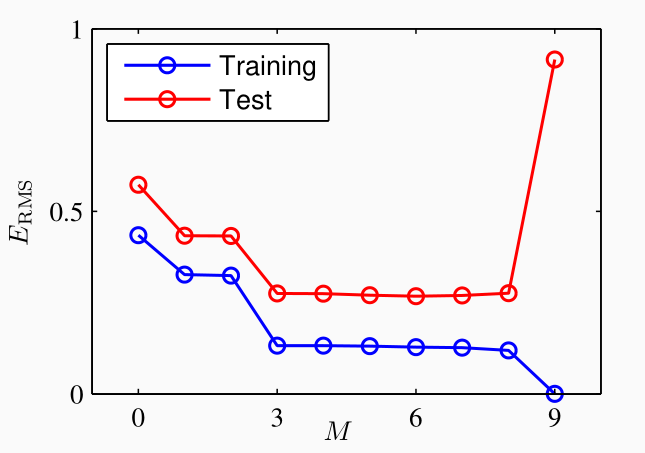
notiamo che inizialmente al crescere di \(M\) l'errore sia sul training set che sul test set diminuisce. Ad un certo punto però se aumentiamo ancora \(M\) succede che l'errore sul training set tende a \(0\), mentre quello sul test set tende ad aumentare molto. Questo effetto di "risalita" è proprio una conseguenza dell'overfitting.
Per limitare la complessità del nostro modello in modo da non cadere in situazioni di overfitting si può utilizzare una tecnica di regolarizzazione. Questa tecnica consiste nell'introdurre un termine aggiunto nella funzione di errore il cui ruolo è proprio quello di limitare la complessità.
Un tipico approccio alla regolarizzazione è quello di limitare il modulo dei valori dei coefficienti modificando la funzione di errore nel seguente modo
\[\begin{split} \tilde{E}(\mathbf{w}) &= \frac12 \sum\limits_{i = 1}^n (y(x_i, \mathbf{w}) - t_i)^2 + \frac{\lambda}{2} \sum\limits_{k = 0}^M w_k^2 \\ &= \frac12 \sum\limits_{i = 1}^n (y(x_i, \mathbf{w}) - t_i)^2 + \frac{\lambda}{2} ||\mathbf{w}||^2 \end{split}\]
Notiamo come questo limite non viene imposto "dall'alto", ovvero limitando a priori il valore dei coefficienti, bensì viene introdotto in modo implicito, andando ad aumentare l'errore nei modelli più complessi.
Observation: Il fattore di regolarizzazione in cui utilizziamo il quadrato dei coefficienti è chiamato ridge (regression). Tra le possibili alternative troviamo il fattore lasso, che invece consiste nel calcolare il modulo dei coefficienti \(\sum_{k = 0}^M |w_k|\).
Il parametro \(\lambda\) nel fattore di regolarizzazione è un iper-parametro del nostro modello, in quanto ci permette di determinare quanta regolarizzazione vogliamo fare: quanto maggiore è l'ambda tanto più il secondo termine vale rispetto al primo.
