ML - 03 - Probability/Statistics Review
Date:
Lecturer: Giorgio Gambosi
Slides: (ml_02_probstat-slides.pdf)
Table of contents:
In questa lezione abbiamo ripassato alcuni concetti base di probabilità e statistica.
Per quanto riguarda le variabili aleatorie discrete, ovvero per le variabili che assumono valori in insiemi finiti o al più numerabili, i seguenti concetti sono da ricordare:
Probability mass function (pmf).
Joint and conditional probabilities.
Union of events
Product rule
Sum rule and marginalization
\[p(x) = \sum_{y \in \mathcal{Y}} p(x, y) = \sum_{y \in \mathcal{Y}} p(x|y) \cdot p(y)\]
Bayes Rule
\[p(x|y) = \frac{p(y|x)p(x)}{p(y)} = \frac{p(y|x)p(x)}{\sum_{x \in \chi} p(y|x)p(x)}\]
in cui si utilizza la seguente terminologia:
\(p(x)\) è detta prior probability of \(x\).
\(p(x|y)\) è detta posterior of \(x\).
\(p(y|x)\) è detta likelihood of \(y\) given \(x\).
\(p(y)\) è detta evidence di \(y\).
Indipendence
\[p(x, y) = p(x) \cdot p(y)\]
Conditional independence
\[p(x,y|z) = p(x|z) \cdot p(y|z)\]
Per le variabili aleatorie continue invece i seguenti concetti sono da ripassare:
Cumulative distribution function (cdf).
\[\begin{split} F(x) &= P(X \leq x) \\ \\ P(a < X \leq b) &= F(b) - F(a) \\ \end{split}\]
Probability density function.
\[\begin{split} f(x) &= \frac{d}{dx} F(x) \\ \\ P(a < X \leq b) &= \int_{a}^b f(x) dx \\ \\ P(x < X < x + dx) &= f(x)dx \,\,\,\,\, \text{(for } dx \text{ sufficiently small)} \end{split}\]
Sum rule
\[f(x) = \int_{\mathcal{Y}}f(x, y) dy = \int_{y \in \mathcal{Y}} f(x|y) \cdot f(y) dy\]
Nel caso discreto
\[\begin{split} \mathbb{E}_p[g(x)] &= \sum_{x \in V_x}g(x) p(x) \,\,\,\, &\text{(caso discreto)} \\ \mathbb{E}_f[g(x)] &= \int_{-\infty}^{\infty} g(x)f(x) dx \,\,\,\, &\text{(caso continuo)} \\ \end{split}\]
Nel caso in cui \(g(x) = x\) abbiamo il valore medio
\[\begin{split} \mathbb{E}_p[x] &= \sum_{x \in V_x}x p(x) \,\,\,\, &\text{(caso discreto)} \\ \\ \mathbb{E}_f[x] &= \int_{-\infty}^{\infty} x f(x) dx \,\,\,\, &\text{(caso continuo)} \\ \end{split}\]
Il valore atteso ha le seguenti proprietà:
Per ogni \(a \in \mathbb{R}\): \(\mathbb{E}[a] = [a]\).
Per ogni \(a \in \mathbb{R}\): \(\mathbb{E}[af(x)] = a \mathbb{E}[f(x)]\).
\(\mathbb{E}[f(x) + g(x)] = \mathbb{E}[f(x)] + \mathbb{E}[g(x)]\).
Definita da
\[Var[X] = \mathbb{E}[(x - \mathbb{E}[x])^2]\]
o, equivalentemente,
\[Var[X] = \mathbb{E}[x^2] - \mathbb{E}[x]^2\]
ha le seguenti proprietà
Per ogni \(a \in \mathbb{R}\): \(Var[a] = 0\).
Per ogni \(a \in \mathbb{R}\): \(Var[af(x)] = a^2 Var[f(x)]\).
Le seguenti distribuzioni sono di interesse e devono essere ricordate:
Bernoulli distribution, Bern(\(p\))
\[\begin{split} x \in \{0, 1\} \\ \\ p(x) = \begin{cases} p \,\,&,\,\, x = 1 \\ p \,\,&,\,\, x = 0 \\ \end{cases} \\ \\ p(x) = p^x (1-p)^{1-x} \\ \\ \mathbb{E}[x] = p \,\,\,,\,\,\, Var[x] = p(1-p) \end{split}\]
Categorial distribution
\[p(x) = \prod\limits_{j = 1}^k p_j^{x_j}\]
Binomial distribution
\[p(x) = \binom{n}{x}p^x(1-p)^{n-x} = \frac{n!}{x!(n-x)!}p^x (1-p)^{n-x}\]
Poisson distribution
\[p(x) = e^{-\lambda}\frac{\lambda^x}{x!}\]
Normal (gaussian) distribution
\[f(x) = \frac{1}{\sqrt{2 \pi \sigma}} e^{\frac{(x-\mu)^2}{2\sigma^2}}\]
Beta distribution, Beta(\(\alpha, \beta\))
Questa distribuzione ci interessa in quanto ci permette di definire una variabile casuale che assumi valori tra \(0\) e \(1\).
\[\begin{split} f(x) &= \frac{\Gamma(\alpha + \beta)}{\Gamma(\alpha) \Gamma(\beta)} x^{\alpha - 1} (1 - x)^{\beta - 1} \\ \\ \Gamma(x) &j= \int_0^{\infty} u^{x-1}e^u \,\,du \\ \end{split}\]
Le distribuzioni multivariate sono definite su più di una variabile casuale.
È possibile estendere il concetto di cumulative joint distribution anche al caso multivariato
\[F(x, y) = P(X leq x, Y \leq y)\]
Se \(F(x, y)\) è derivabile in ogni punto rispetto sia a \(x\) che a \(y\) è possibile definire la joint probability density come segue
\[f(x, y) = \frac{\partial^2 F(x,y)}{\partial x \partial y}\]
e quindi
\[P((X, Y) \in A) = \int\int_{(x, y) \in A} f(x, y) \,\, dx dy\]
Il concetto di covarianza ci fornisce un modo per stimare quanto le variazioni di due variabili casuali siano collegate (linearmente) tra loro.
\[Cov[X, Y] = \mathbb{E}[(X - \mathbb{E}[X])(Y - \mathbb{E}[Y])]\]
o, equivalentemente,
\[Cov[X, Y] = \mathbb{E}[XY] - \mathbb{E}[X] \mathbb{E}[Y]\]
Per la covarianza valgono le seguenti proprietà:
$Var[X + Y] = Var[X] + Var[Y] + 2Cov[X, Y]$$
Se \(X\) e \(Y\) sono indipendenti, allora \(Cov[X, Y] = 0\).
Siano \(X_1, X_2, \ldots, X_N\) è un insieme di variabili casuali. Allora definiamo un vettore casuale (random vector), come segue
\[\mathbf{x} = \begin{bmatrix} X_1 \\ X_2 \\ \vdots \\ X_n \end{bmatrix}\]
Se poi abbiamo una funzione \(g:\mathbb{R}^n \to \mathbb{R}^m\), allora possiamo applicare la funzione al vettore per ottenere un vettore di funzioni come segue
\[g(\mathbf{x}) = \begin{bmatrix} g_1(\mathbf{x}) \\ g_2(\mathbf{x}) \\ \vdots \\ g_m(\mathbf{x}) \end{bmatrix}\]
dove \(\mathbf{x} \in \mathbb{R}^n\).
Dato un vettore random \(\mathbf{x} \in \mathbb{R}^n\), la sua matrice di covarianza \(\Sigma\) è una matrice \(n \times n\) tale che
\[\Sigma_{i, j} = Cov[X_i, X_j]\]
Ovvero,
\[\begin{split} \Sigma &= \begin{bmatrix} Cov[X_1, X_1] & Cov[X_1, X_2] & \ldots & Cov[X_1, X_n] \\ Cov[X_2, X_1] & Cov[X_2, X_2] & \ldots & Cov[X_2, X_n] \\ \ldots & \ldots & \ddots & \ldots \\ Cov[X_n, X_1] & Cov[X_n, X_2] & \ldots & Cov[X_n, X_n] \\ \end{bmatrix} \\ \\ &= \begin{bmatrix} Var[X_1] & Cov[X_1, X_2] & \ldots & Cov[X_1, X_n] \\ Cov[X_2, X_1] & Var[X_2] & \ldots & Cov[X_2, X_n] \\ \ldots & \ldots & \ddots & \ldots \\ Cov[X_n, X_1] & Cov[X_n, X_2] & \ldots & Var[X_n] \\ \end{bmatrix} \\ \end{split}\]
Equivalentemente,
\[\Sigma = \mathbb{E}[XX^T] - \mathbf{\mu}\mathbf{\mu}^T\]
Dove \(\mathbf{\mu} = \begin{pmatrix} \mu_1 & \ldots & \mu_n \end{pmatrix}^T\).
La matrice di covarianza ha le seguenti proprietà:
È semidefinita positiva, ovvero
\[\mathbf{z}^T \Sigma \mathbf{z} \geq 0\]
per ogni \(\mathbf{z} \in \mathbb{R}^n\).
È simmetrica, ovvero
\[Cov[X_i, X_j] = Cov[X_j, X_i]\]
Strettamente collegata al concetto di covariance matrix troviamo la correlation matrix, che è ottenuta applicando ad ogni coppia di v.a. il coefficiente di correlazione di Pearson, detto anche Person correlation coefficient
\[\rho_{X, Y} = \frac{Cov[X, Y]}{\sqrt{Var[X] \cdot Var[Y]}}\]
Notiamo le seguenti cose:
Se \(Y = aX + b\), allora
\[\begin{split} Cov[X, Y] &= \mathbb{E}[(X - \mu)(aX + b - a \mu - b)] \\ &= \mathbb{E}[a(X - \mu)^2] \\ &= a Var[X] \\ \end{split}\]
e dato che
\[Var[Y] = (aX - a\mu)^2 = a^2Var[X]\]
ne consegue che \(\rho_{X, Y} = 1\).
Se invece \(X\) e \(Y\) sono indipendenti, allora si ha che \(\rho_{X, Y} = 0\). Dunque, variabili indipendenti hanno una correlazione nulla.
Il contrario dell'ultima affermazione però non è vero: avere una correlazione nulla non implica essere indipendenti, come mostra il caso in cui abbiamo \(X\) uniforme in \([-1, 1]\) e \(Y = X^2\). Questo è una conseguenza del fatto che il concetto di correlazione corrisponde ad una dipendenza di tipo lineare tra le variaibli, che è quindi un caso particolare di dipendenza.
La matrice di correlazione è quindi fatta così
\[\begin{split} \mathbf{\Sigma} &= \begin{bmatrix} \rho_{X_1, X_1} & \rho_{X_1, X_2} & \ldots & \rho_{X_1, X_n} \\ \rho_{X_2, X_1} & \rho_{X_2, X_2} & \ldots & \rho_{X_2, X_n} \\ \ldots & \ldots & \ddots & \ldots \\ \rho_{X_n, X_1} & \rho_{X_n, X_2} & \ldots & \rho_{X_n, X_n} \\ \end{bmatrix} = \begin{bmatrix} 1 & \rho_{X_1, X_2} & \ldots & \rho_{X_1, X_n} \\ \rho_{X_2, X_1} & 1 & \ldots & \rho_{X_2, X_n} \\ \ldots & \ldots & \ddots & \ldots \\ \rho_{X_n, X_1} & \rho_{X_n, X_2} & \ldots & 1 \\ \end{bmatrix} \end{split}\]
Un'estensione al caso multivariato della distribuzione binomiale è la distribuzione multinomiale.
\[p(x_1, \ldots, x_k) = \frac{n!}{x_1! \ldots x_k!} \prod\limits_{i = 1}^k p_i^{x_i}\]
con
\[\sum_{i = 1}^k x_i = n\]
La ditributon di dirichlet è l'estensione al caso multivariato della distribuzione beta.
\[f(x_1, \ldots, x_k) = \frac{\Gamma(\sum_{i = 1}^k \alpha_i)}{\prod_{i = 1}^k \Gamma(\alpha_i)} \prod\limits_{i = 1}^k x_i^{\alpha_i - 1} = \frac{1}{\Delta(\alpha_1, \ldots, \alpha_k)} \prod\limits_{i = 1}^k x_i^{\alpha_i - 1}\]
dove
\[\sum\limits_{i = 1}^k x_i = 1\]
La distribuzione gaussiana ha una serie di caratteristiche utili, tra cui troviamo:
È analiticamente trattabile.
È completamente specificata dai primi due momenti (media e varianza).
Permette di modellare un determinato numero di processi stocastici (teorema del limite centrale).
Trasformazioni lineare di gaussiane ci forniscono altre gaussiane.
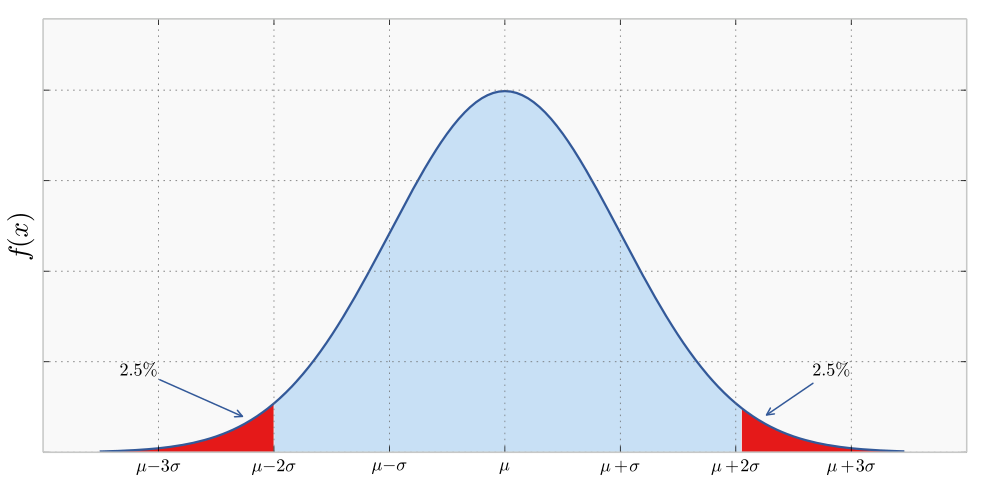
Come avevamo già visto, nel caso univariato la distribuzione gaussiana \(\mathcal{N}(\mu, \sigma^2)\) è definita come segue per ogni \(x \in \mathbb{R}\)
\[f(x) = \frac{1}{\sqrt{2 \pi \sigma}}e^{-\frac{(x - \mu)^2}{2\sigma^2}}\]
ed è rappresentata così
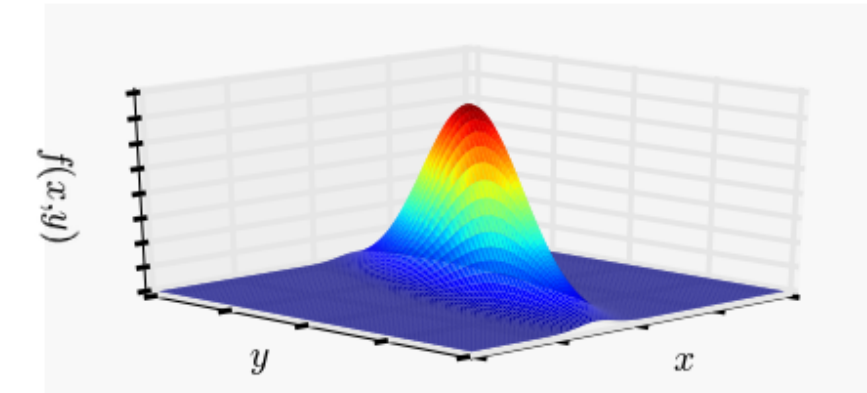
Nel caso di una gaussiana multivariata \(\mathcal{N}(\mathbf{\mu}, \mathbf{\Sigma})\) invece abbiamo che per ogni \(x \in \mathbb{R}^d\)
\[f(x) = \frac{1}{(2 \pi)^{d/2} |\mathbf{\Sigma}|^{1/2}}e^{-\frac12 \cdot (\mathbf{x} - \mathbf{\mu})^T \mathbf{\Sigma}^{-1}(\mathbf{x} - \mathbf{\mu})}\]
dove \(\mathbf{\mu}\) è il vettore dei valori attesi, mentre \(\mathbf{\Sigma}\) è la matrice \(d \times d\) delle covarianze \(\sigma_{i, j} = \mathbb{E}[(X_i - \mu_i)(X_j - \mu_j)]\).
Graficamente abbiamo,
Mentre la media definisce dove è posizionata la distribuzione di probabilità, la struttura della matrice di covarianza di covarianza mi definisce la forma della distribuzione. Tra le varie strutture troviamo le seguenti di particolare interesse:
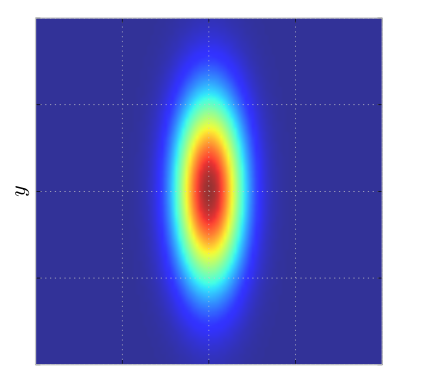
Diagonal covariance matrix: Se la matrice di covarianza è diagonale, ovvero se la covarianza tra le variabili è nulla
\[\mathbf{\Sigma} = \begin{bmatrix} \sigma_1^2 & 0 & \ldots & 0 \\ 0 & \sigma_2^2 & \ldots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \ldots & \sigma_n^2 \\ \end{bmatrix}\]
Allora la distribuzione di probabilità tende ad assumre una forma di questo tipo, ovvero tende ad essere orientata lungo gli assi.
Identity covariance matrix: Nel caso in cui la matrice di covarianza sia una matrice identità moltiplicata per una costante, allora abbiamo
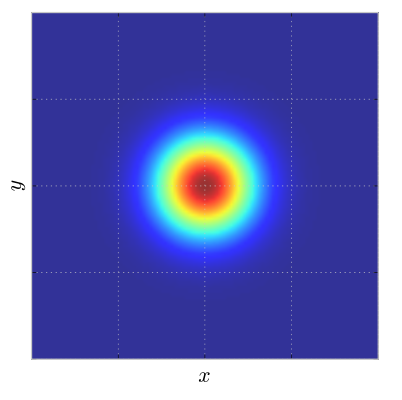
Possiamo vedere una generica distribuzione gaussiana rispetto alla decomposizione spettrale della matrice di covarianza.
Nel caso di una gaussiana multivarata possiamo vedere che gli assi della gaussiana sono orientati secondo gli autovettori della matrice di covarianza.
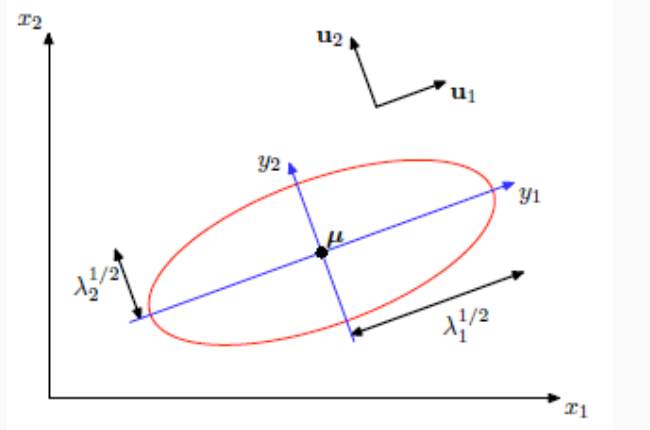
Se prendiamo un vettore normale distribuito gaussiano e applichiamo una trasformazione lineare, anche il risultato è un vettore gaussiano.
\[x \sim \mathcal{N}(\mathbf{\mu}, \mathbf{\Sigma}) \implies y \sim \mathcal{N}(A^T \mathbf{\mu}, A^T \Sigma A)\]
dove \(y = A^T x\) e \(x\) è un vettore normalmente distribuito.