ML - 05 - Information Theory
Date:
Lecturer: Giorgio Gambosi
Slides: (ml_02_probstat-slides.pdf)
Table of contents:
In questa lezione concludiamo il ripasso della probabilità e statistica ricordando qualche concetto ripreso dalla teoria dell'informazione.
Sia \(X\) è una v.a. discreta causale, vogliamo definire una misura \(h(x)\) dell'informazione che ci fornisce l'osservazione \(X=x\). In questo contesto misuriamo l'informazione di un evento rispetto alla "sorpresa" che proviamo nell'osservare quell'evento.
Questa misura \(h(x)\) deve rispettare i seguenti requisiti:
Gli eventi molto probabili suscitano una sorpresa molto bassa, se osservati, mentre quelli poco probabili suscitano una sorpresa molto alta. Otteniamo quindi che \(h(x)\) è inversamente proporzionale a \(P(x)\).
Se \(X\) e \(Y\) sono indipendenti, l'evento \((X = x \,\,\,,\,\,\, Y = y)\) ha probabilità \(P(x)P(y)\), mentre la "sorpresa" dell'evento è la somma delle sorprese dei due eventi. In formula,
\[h(x, y) = h(x) + h(y)\]
Una funzione che rispetta questi vincoli è la funzione logaritmica, tipicamente scelta in base \(2\).
\[h(x) = - \log_2 x\]
L'entropia della v.a. \(X\) è quindi definita come l'informazione attessa di tutti i possibili valori assunti da \(X\).
\[H(X) = - \sum\limits_x P(x) \cdot \log_2 P(x)\]
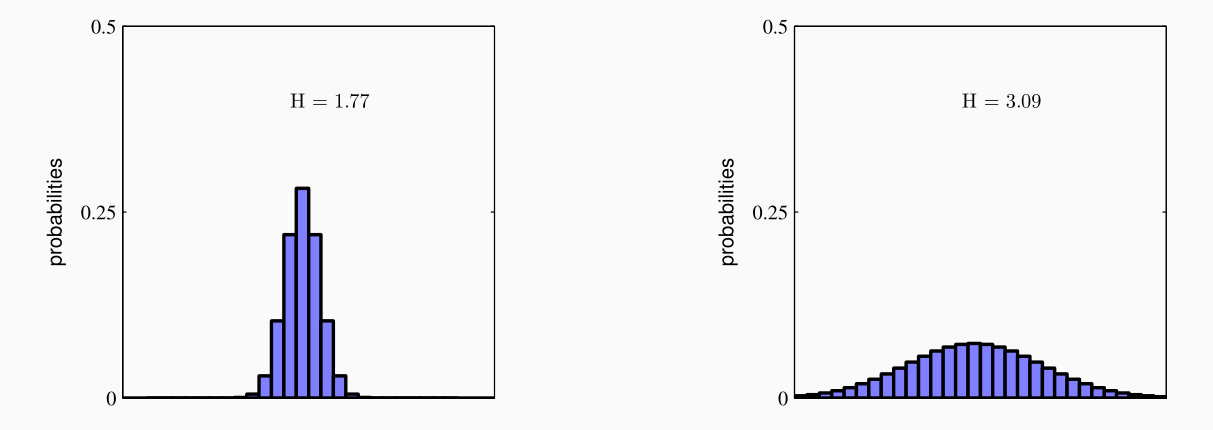
Notiamo come l'entropia è una grandezza associata ad una v.a. e viene utilizzata per misurare l'incertezza associata ad \(X\). Più bassa è l'entropia e più \(X\) seguirà una "peaked distribution", ovvero una distribuzione concentrata sul valore atteso. L'entropia è massimizzata quando \(X\) segue una distribuzione uniforme.
Banalmente valgono le seguenti proprietà per l'entropia di una v.a. discreta \(X\):
Dato che \(P(x) \in [0, 1]\), alora \(P(x) \cdot \log_2 P(x) \leq 0\) e quindi \(H(X) \geq 0\).
\(H(X) = 0\) se esiste un \(x\) tale che \(P(x) = 1\).
L'entropia è massimizzata si ha nel caso in cui la distribuzione di \(X\) è uniforme. In tal caso \(H(X) = \log_2 k\), dove \(k\) è il numero di eventi.
\(H(X)\) ci da un lower bound rispetto al numero atteso di bits che possono essere utilizzati per codificare i valori di \(X\).
Supponiamo di avere due v.a. discrete \(X\) e \(Y\). La quantità attessa di informazione aggiuntiva necessaria per specificare il valore di \(Y\) conoscendo il valore di \(X\) è nota come conditional entropy (entropia condizionata) di \(Y\) dato \(X\), ed è così definita
\[H(Y|X) = - \sum\limits_x \sum\limits_y P(x, y) \cdot \ln P(y | x)\]
Dato che \(\ln P(y|x) = \ln P(x,y) - \ln P(x)\) ne consegue che
\[H(X, Y) = H(Y|X) + H(X)\]
Assumiamo di non conoscere la distribuzione \(P(x)\) della v.a. \(X\) e di avere solo una approssimazione \(Q(x)\) di tale distribuzione.
Se utilizziamo la distribuzone \(Q(x)\) per codificare i valori di \(X\) la lunghezza media di tale codifica sarà
\[- \sum_x P(x) \cdot \ln Q(x)\]
mentre la lunghezza media minima, quella ottenuta conoscendo \(P(x)\), è di
\[-\sum_x P(x) \cdot \ln P(x)\]
Ora, la quantità di informazione aggiuntiva utilizzata per codificare i valori di \(X\) utilizzando l'approssimazione \(Q(x)\) rispetto alla distribuzione corretta \(P(x)\) prende il nome di Kullback-Leibler divergence, ed è così definita
\[\begin{split} KL(P||Q) &= - \sum\limits_x P(x) \cdot \ln Q(x) + \sum\limits_x P(x) \cdot \ln P(x) \\ &= -\sum\limits_x P(x) \cdot \ln \frac{P(x)}{Q(x)} \\ \end{split}\]
Il valore \(KL(P||Q)\) misura la differenza tra le distribuzioni \(P\) e \(Q\). Valgono quindi le seguenti proprietà:
\(KL(P||Q) = 0\)
\(KL(P||Q) \neq KL(Q||P)\), ovvero la funzione non è simmetrica e quindi non può essere utilizzata come misura di distanza.
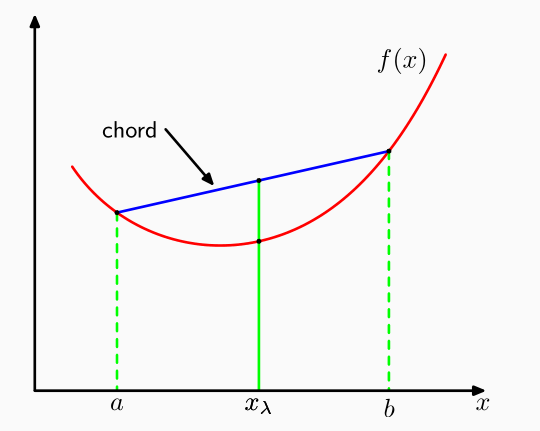
Una funzione è detta convessa in un'intervallo \([a, b]\) se per ogni valore di \(0 \leq \lambda \leq 1\) vale
\[f(\lambda a + (1 - \lambda b)) \leq \lambda f(a) + (1 - \lambda) f(b)\]
Graficamente,
Se \(f(x)\) è una funzione convessa, allora vale la Jensen's inequality per ogni punto \(x_1, \ldots, x_M\), che ci dice che
\[f\bigg(\sum\limits_{i = 1}^M \lambda_i x_i\bigg) \leq \sum\limits_{i = 1}^M \lambda_i f(x_i)\]
dove \(\lambda_i \geq 0\) per ogni \(i\) e \(\sum_{i = 1}^M \lambda_i = 1\).
Casi particolari in cui è possibile applicare questa diseguaglianza sono:
Se \(\lambda_i = P(x_i)\), troviamo
\[f(\mathbb{E}[x]) \leq \mathbb{E}[f(x)]\]
Se \(x\) è una v.a. continua, troviamo
\[f\bigg(\int x P(x) dx\bigg) \leq \int f(x) P(x) dx\]
Dato che la funzione logaritmo è convessa, applicandola a \(KL(P||Q)\) otteniamo
\[KL(P||Q) = - \int P(x) \cdot \ln{\frac{Q(x)}{P(x)}} dx \geq - \ln{\int Q(x) dx} = 0\]
e quindi \(KL\) è sempre non negativa.
Consideriamo un dataset \(\mathbf{x} = \begin{pmatrix} x_1, & \ldots &, x_n \end{pmatrix}\) generato da una distribuzione a noi sconosciuta \(P(x)\). Vogliamo modellare questa situazione utilizzando un modello probabilistico \(Q_\theta(x|\Theta)\) istanziato con un parametor \(\Theta\).
L'idea quindi è di derivare i parametri del modello che meglio ci permettono di rappresentare il dataset osservato \(\mathbf{x}\). Una possibile idea è quindi quella di minimizzare la KL rispetto ai dati a nostra disposizione
\[\begin{split} KL(P||Q_{\Theta}) &= - \sum\limits_x P(x) \cdot \ln{\frac{Q(x|\Theta)}{P(X)}} \\ &\approx - \frac{1}{n} \sum\limits_{i = 1}^n \ln{\frac{Q(x_i|\Theta)}{P(x_i)}} \\ &= \frac{1}{n} \sum\limits_{i = 1}^n \Big( \ln P(x_i) - \ln Q(x_i | \Theta) \Big) \\ \end{split}\]
Notiamo che il primo termine è indipendente da \(\Theta\), mentre il secondo termine è la log-likelihood di \(\mathbf{x}\) negata. Il valore del parametro \(\Theta\) che minimizza \(KL(P||Q_{\Theta})\) è dunque anche il valore che massimizza la log-likelihood.
La mutual information è una misura di indipendenza tra due v.a. discrete \(X\) e \(Y\), ed è definita come segue
\[\begin{split} I(X, Y) &= KL(P(X, Y) \,\, || \,\, P(X) \cdot P(Y)) \\ &= -\sum_x \sum_y P(x, y) \cdot \ln{\frac{P(x) P(y)}{P(x, y)}} \end{split}\]
Questa misura rappresenta quanto perdiamo nel momento in cui noi assumiamo l'indipendenza rispetto alla distribuzione effettiva. \(I(X, Y)\) tende ad essere tanto più bassa quanto più la distribuzione congiunta assomiglia al prodotto delle due distribuzioni, ovvero quanto più le due v.a. tendono ad essere indipendenti.
È possibile dimostrare le seguenti relazioni
\[\begin{split} I(X, Y) &= H(X) - H(X|Y) \\ I(X, Y) &= H(Y) - H(Y|X) \\ \end{split}\]
Observation: La mutual information può essere utilizzata per misurare la rilevanza che una particolare feature di un dataset ha nella classificazione. Per fare questo infatti basta calcolarsi la mutual information tra la feature in questione e il target.