ML - 06 - Model Inference
Date:
Lecturer: Giorgio Gambosi
Slides: (ml_03_modinf-slides.pdf)
In questa lezione introduciamo alcuni concetti fondamentali nell'inferenza dei modelli.
Inferire un modello probabilistico da una collezione di dati osservati \(\mathbf{X} = \{x_1, \ldots, x_n\}\) significa trovare una particolare distribuzione di probabilità sul dominio dei dati. Un modello probabilistico quindi può essere visto come una descrizione più compatta del dataset dal quale è possibile estrarre dell'informazione statistica/probabilistica.
Un dataset \(\mathbf{X}\) è una collezione di un certo numero \(N\) di dati osservati, che sono assunti essere indipendenti tra loro e identicamente distribuiti, ovvero possono essere visti come istanziazioni della stessa v.a. che assume valori rispetto alla sua distribuzione.
Quando facciamo model inference quindi vogliamo partire dai dati e arrivare ad un modello probabilisto.
\[X \longrightarrow \mathcal{M}\]
Questo problema può essere decomposto in tre sottoproblemi, che sono:
Model selection: In questa fase si individua un modello probabilisto \(\mathcal{M}\) che meglio può rappresentare una data collezione di dati osservati \(\mathbf{X}\). Questi modelli possono essere distribuzioni di probabilità o processi probabilistici. In generale sono modelli parametrizzati da un insieme di valori, detti appunto parametri.
Estimation: Fissate le caratteristiche di un modello probabilistico, in questa seconda fase si cerca di stimare i valori dei parametri \(\mathbf{\Theta} = (\theta_1, \ldots, \theta_D)\) del modello che spiegano nel modo migliore possibile i dati osservati.
Prediction: Alla fine si utilizza il modello per calcolare la probabilità di una nuova osservazione \(P(x|\mathbf{X})\) utilizzando i dati già osservati.
Notiamo come, alla fin fine, la parte più importante è quella della prediction, in quanto il nostro obiettivo finale è proprio quello di fare delle predizioni rispetti ai dati già osservati.
In quest'ambito parleremo quasi esclusivamente di apprendimento di tipo Bayesiano.
In questo contesto l'attività di selezione di un modello (la model selection) consiste nell'avere uno spazio di possibili modelli \(\mathcal{M}\) predefinito e in cui un modello \(m \in \mathcal{M}\) è una distribuzione di probabilità \(P(\mathbf{x} | m)\) sui dati.
Sia quindi \(P(m)\) una distribuzione a priori dei modelli, che assegna un valore di probabilità ad ogni modello e tale che
\[\sum\limits_{m \in \mathcal{M}} P(m) = 1\]
Allora la corrispondente distribuzione (a priori )predittiva sui dati è data da
\[P(\mathbf{x}) = \sum\limits_{m \in \mathcal{M}} P(\mathbf{x} | m) \cdot P(m)\]
Quando poi osserivamo un dataset \(\mathbf{X}\) in cui gli eventi sono indipendenti, allora andiamo ad aggiornare le probabilità nel seguente modo
\[\begin{split} P(m | \mathbf{X}) &= \frac{P(m) P(\mathbf{X}|m)}{P(\mathbf{X})} \\ &\propto P(m)P(\mathbf{X}|m) \\ &= P(m) \prod\limits_{i = 1}^n P(x_i | m) \\ \end{split}\]
la distribuzione predittiva a posteriori è quindi data da
\[P(\mathbf{x} | \mathbf{X}) = \sum\limits_{m \in \mathcal{M}} P(\mathbf{x} | m) \cdot P(m | \mathbf{X})\]
Nel caso invece in cui abbiamo dei modelli parametrici in cui quindi la variazione del modello consiste nella variazione di un parametro all'interno di un parameter space \(\mathbf{\Theta}\).
Definita una distribuzione dei parametri a priori \(P(\mathbf{\theta} | m)\) per il modello, la distribuzione predittiva a priori è data da
\[P(\mathbf{x} | m) = \int_{\mathbf{\Theta}} P(\mathbf{x } | \mathbf{\theta}, m) \cdot P(\mathbf{\theta} | m) \,\,\, d \mathbf{\theta}\]
Dopo aver osservato un dataset \(\mathbf{X}\) applicando la formula di Bayes otteniamo
\[P(\mathbf{\theta} | \mathbf{X}, m) = \frac{P(\mathbf{\theta}|m) P(\mathbf{X}|\mathbf{\theta}, m)}{P(\mathbf{X}|m)} \propto P(\mathbf{\theta} | m) \cdot P(\mathbf{X} | \mathbf{\theta}, m)\]
La distribuzione predittiva a posteriori è quindi data da
\[P(\mathbf{x} | \mathbf{X}, m) = \int_{\mathbf{\Theta}} P(\mathbf{x} | \mathbf{\theta}, m) P(\mathbf{\theta} | \mathbf{X}, m) \,\,\, d \mathbf{\theta}\]
Dato un modello \(m\), l'approccio bayesiano cerca di derivare una distribuzione a posteriori dell'insieme dei parametri \(\mathbf{\theta}\). Per fare questo dobbiamo calcolare
\[P(\mathbf{\theta} | \mathbf{X}) = \frac{P(\mathbf{X}| \mathbf{\theta}) P(\mathbf{\theta})}{P(\mathbf{X})} = \frac{P(\mathbf{X} | \mathbf{\theta}) P(\mathbf{\theta})}{\int_{\mathbf{\Theta}} P(\mathbf{X} | \mathbf{\theta}) P(\mathbf{\theta}) \,\, d \mathbf{\theta} }\]
e alla fine otteniamo
\[P(x | \mathbf{X}) = \int_{\mathbf{\theta}} P(x | \mathbf{\theta}) P(\mathbf{\theta} | \mathbf{X}) \,\,\, d \mathbf{\theta}\]
Molto spesso però questo calcolo è difficile da effettuare in modo efficiente, in quanto nel denominatore abbiamo un integrale multidimensionale rispetto a tutti i parametri che entrano in gioco.
Per semplificare questo calcolo l'idea è quella di effettuare una point estimate (stima di punto) dei parametri, che consiste nell'individuare preventivamente un valore specifico da assegnare ai parametri. L'idea quindi è quella di stimare un "migliore" valore \(\hat{\theta}\) nello spazio dei parametri \(\mathbf{\Theta}\), dove per "migliore" lo si intende rispetto a una qualche misura.
Così facendo la distributione predittiva a posteriori può essere approssimata come segue
\[\begin{split} P(x | \mathbf{X}) &= \int_{\mathbf{\Theta}} P(x | \mathbf{\theta}) P(\mathbf{\theta} | \mathbf{X}) \,\,\, d \mathbf{\theta} \\ &\approx \int_{\mathbf{\Theta}} P(x | \hat{\mathbf{\theta}}) P(\mathbf{\theta} | \mathbf{X}) \,\, d \mathbf{X} \\ &= P(x | \hat{\mathbf{\theta}}) \int_{\mathbf{\Theta}} P(\mathbf{\theta} | \mathbf{X}) \,\,\, d \mathbf{\theta} \\ &= P(x | \hat{\mathbf{\theta}}) \end{split}\]
ovvero la predizione è effettuata solamente rispetto al migliore valore dei parametri \(\hat{\theta}\).
L'approccio più utilizzato per selezionare un migliore valore di \(\theta\) è tramite l'utilizzo della stima per massima verosomiglianza. L'approccio in questo caso è un approccio tipicamente frequentista della probabilità, in cui assumiamo che i parametri che vogliamo stimare siano delle variabili deterministiche il cui valore è ignoto e deve essere stimati.
Il valore del parametro di interesse è quindi ottenuto massimizzando l'espressione della likelihood
\[L(\theta | \mathbf{X}) = P(\mathbf{X} | \theta) = \prod\limits_{i = 1}^N P(x_i | \theta)\]
Observation: Tipicamente in probabilità quando scriviamo \(P(\mathbf{x} | \theta)\) consideriamo tale espressione in funzione delle osservazioni \(\mathbf{x}\), dove il valore del parametro \(\theta\) è fissato. In questo caso invece guardiamo l'espressione con un altro punto di vista: l'osservazione \(\mathbf{x}\) è nota e facciamo variare il valore del parametro \(\theta\). È proprio per mettere in evidenza questo scambio di punto di vista che scriviamo \(L(\theta | \mathbf{x})\) al posto di \(P(\mathbf{x} | \theta)\).
Dato che devo massimizzare rispetto a \(\theta\), l'idea è quella di utilizzare le derivate. Dato però che l'espressione della derivata di un prodotto tende ad essere molto complessa, l'idea è quella di considerare la log-likelihood, ovvero di applicare alla funzione \(L(\theta | \mathbf{x})\) il logaritmo (tipicamente in base \(e\)), per otenere
\[l(\theta | \mathbf{X}) = \ln{L(\theta | \mathbf{X})} = \sum\limits_{i = 1}^N \ln{P(x_i | \theta}\]
Dato che la funzione logaritmo è una funzione monotona, essa non cambia il punto di massimo, ovvero
\[\underset{\theta}{\arg\max} \,\,\,\, l(\theta | \mathbf{X}) = \underset{\theta}{\arg\max} \,\,\,\, L(\theta | \mathbf{X})\]
Per trovare il punto di massimo devo quindi risolvere il seguente sistema
\[\forall i = 1, \ldots, D: \,\,\, \frac{\partial l(\theta | \mathbf{X})}{\partial \theta_i} = 0\]
o, in modo più coinciso, utilizzando la notazione del gradiente,
\[\Delta_{\theta} \,\,\, l(\theta | \mathbf{X}) = \mathbf{0}\]
Supponiamo che \(\mathbf{X}\) sia un dataset che contiene \(n\) eventi binari (lanci di moneta) e supponiamo di voler modellare tale dataset con una distribuzione di Bernoulli di cui non conosciamo il parametro \(\phi\). Abbiamo già visto che
\[P(x | \phi) = \phi^x (1 - \phi)^{1-x}\]
La verosimiglianza (likelihood) è quindi
\[L(\phi | \mathbf{X}) = \prod\limits_{i = 1}^N \phi^{x_i} (1 - \phi)^{1 - x_i}\]
Mentre la log-likelihood è data da
\[\begin{split} l(\phi | \mathbf{X}) &= \sum\limits_{i = 1}^N x_i \ln{\phi} + (1 - x_i) \ln{(1 - \phi)} \\ &= N_1 \ln{\phi} + N_0 \cdot \ln{(1 - \phi)} \\ \end{split}\]
Dove \(N_0\) è il numero di lanci in cui è uscito testa e \(N_1\) è il numero di volte in cui è uscito croce e tali che \(N_0 + N_1 = n\). Per massimiare quest'ultima espressione procediamo quindi con il calcolo della derivata
\[\frac{\partial \,\, l(\phi | \mathbf{X})}{\partial \phi} = \frac{N_1}{\phi} - \frac{N_0}{1 - \phi}\]
Impostando la derivata uguale a \(0\) otteniamo infine
\[\hat{\phi}_{\text{ML}} = \frac{N_1}{N_0 + N_1} = \frac{N_1}{N}\]
che è proprio la stima naturale e intuitiva che avrei dato.
La filosofia dietro alla massima verosimiglianza è proprio quella di trovare il valore del parametro \(\hat{\theta}\) che meglio descriva il dataset osservato \(\mathbf{X}\). Questo non è sempre una cosa positiva, in quanto già nelle lezioni precedenti abbiamo menzionato il fatto che se costruiamo un modello che spiega troppo bene i dati osservati potremmo cadere in una situazione di overfitting, in quanto il modello da noi ottenuto potrebbe essere troppo specializzato per i dati osservati e potrebbe non generalizzare bene.
Per evitare questo problema si introduce quindi un'ulteriore funzione \(P(\theta)\) chiamata penalty function, il cui compito è quello di limitare la complessità del modello e così facendo impedire di entrare in situazioni di overfitting. Così facendo quindi la funzione da massimizzare è la seguente
\[C(\theta | \mathbf{X}) = l(\theta | \mathbf{X}) - P(\theta)\]
Molto spesso come pentalty function è utilizzata una funzione proporzionale alla norma euclidea del vettore dei parametri. In formula,
\[P(\theta) = \frac{\gamma}{2} || \theta ||^2\]
dove \(\gamma\) è un parametro di tuning.
Un approccio diverso rispetto alla maximum-likelihood che ci permette nuovamente di effettuare una point estimate è quello della maximum a posteriori (MAP). Questo approccio è un approccio bayesiano, in cui il parametro da stimare \(\theta\) è visto come una variabile random la cui distribuzione deve essere ottenuta combinanto i dati osservati con la nostra conoscenza a priori del parametro.
In questo caso si calcola il valore del parametro che massimizza la seguente espressione
\[P(\theta | \mathbf{X}) = \frac{P(X | \theta) P(\theta)}{P(\mathbf{X})}\]
Notiamo che nell'espressione di prima il denominatore non dipende da \(\theta\). Possiamo quindi semplificare il calcolo e ottenere
\[\begin{split} \theta_{\text{MAP}} & = \underset{\theta}{\arg\max} \,\,\,\, P(\theta | \mathbf{X}) \\ &= \underset{\theta}{\arg\max} \,\,\,\, \frac{P(\mathbf{X} | \theta) P(\theta)}{P(\mathbf{X})} \\ &= \underset{\theta}{\arg\max} \,\,\,\, P(\mathbf{X} | \theta) P(\theta) \\ &= \underset{\theta}{\arg\max} \,\,\,\, L(\theta | \mathbf{X}) P(\theta) \\ &= \underset{\theta}{\arg\max} \,\,\,\, \ln{(L(\theta | \mathbf{X}) \cdot P(\theta))} \\ &= \underset{\theta}{\arg\max} \,\,\,\, l(\theta | \mathbf{X}) + \ln P(\theta) \\ &= \underset{\theta}{\arg\max} \,\,\,\, \Bigg( \sum\limits_{i = 1}^N \ln{P(x_i | \theta) + \ln{P(\theta)}}\Bigg) \\ \end{split}\]
Consideriamo sempre un dataset \(\mathbf{X}\) che contiene il risutlato di \(n\) lanci di moneta modellati tramite una Bernoulli di parametro \(\phi\), dove questa volta il parametro è modellato come una distribuzione beta
\[P(\phi | \alpha, \beta) = \frac{\Gamma(\alpha + \beta)}{\Gamma(\alpha) + \Gamma(\beta)} \phi^{\alpha - 1} ( 1- \phi)^{\beta - 1}\]
Calcolando la log-likelihood otteniamo
\[\begin{split} l(\phi | \mathbf{X}) &= \sum\limits_{i = 1}^N x_i \ln(\phi) + (1 - x_i) \ln{(1 - \phi)} \\ &= N_1 \ln \phi + N_0\ln{(1 - \phi)} \end{split}\]
Calcolando la derivata invece ottiamo
\[\frac{\partial }{\partial \phi} \,\, \Big[l(\phi | \mathbf{X}) + \ln Beta(\phi | \alpha, \beta)\Big] = \frac{N_1}{\phi} - \frac{N_0}{(1 - \phi)} + \frac{\alpha - 1}{\phi} - \frac{\beta - 1}{1 - \phi}\]
Impostando la derivata uguale a \(0\) e risolvendo per \(phi\) otteniamo quindi
\[\begin{split} \hat{\phi}_{\text{MAP}} &= \frac{N_1 + \alpha - 1}{N_0 + N_1 + \alpha + \beta - 2} \\ &= \frac{N_1 + \alpha - 1}{N + \alpha + \beta - 2} \\ \end{split}\]
Notiamo che applicando la calcolando il parametro tramite la MAP si potrebbe incorrere in problemi di precisione quando la distribuzione ha delle forme particolari.
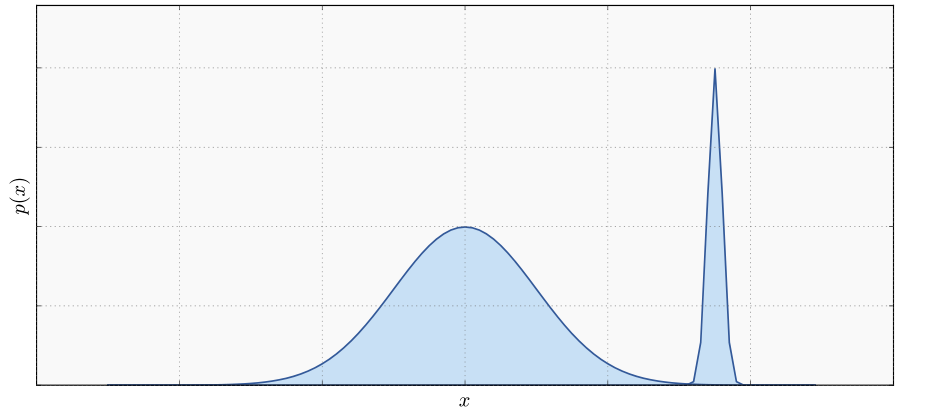
Per evitare questi problemi si potrebbe pensare di prendere il valore atteso di \(\theta\) rispetto a \(P(\theta | \mathbf{X})\).
\[\theta^* = \mathbb{E}_{p(\theta | \mathbf{X})}[\theta] = \int_{\theta} \theta P(\theta | \mathbf{X}) \,\,\, d \theta\]
Il costo da pagare per calcolare la media piuttosto che la moda è che adesso, al posto di calcolare delle derivate, dobbiamo risolvere un integrale.
In generale un altro approccio possibile è a partire dai dati osservati, cerchiamo di derivare una rappresentazione dell'intera distribuzione a posteirori.
Ad esempio, se consideriamo sempre il solito dataset \(\mathbf{X}\) che modella \(n\) lanci di moneta, ciascuno dei quali segue una Bernoulli distribuita con un parametro \(\phi\), che a sua volta è modellato da una \(Beta(\alpha, \phi)\) allora possiamo calcolare l'intera distribuzione a posteriori
\[\begin{split} P(\phi | \mathbf{X}, \alpha, \beta) &= \frac{\prod_{i = 1}^N \phi^{x_i}(1 - \phi)^{1 - x_i} P(\phi | \alpha, \beta)}{P(\mathbf{X})} \\ &= \frac{\phi^{N_1}(1-\phi)^{N_0} \phi^{\alpha-1} (1 - \phi)^{\beta - 1}}{\frac{\Gamma(\alpha) \Gamma(\beta)}{\Gamma(\alpha + \beta)} P(\mathbf{X})} \\ &= \frac{\phi^{N_1 + \alpha - 1} (1 - \phi)^{N_0 + \beta - 1}}{Z} \\ \end{split}\]
dunque otteniamo che
\[P(\phi | \mathbf{X}, \alpha, \beta) = Beta(\phi | \alpha + N_1, \beta + N_0)\]
E a partire da questa possiamo poi utilizzare delle informazioni specifiche sulla distribuzione per ottenere ciò che vogliamo, ovvero la probabilità di predizione a posteriori.
Osservazione: Abbiamo modellato il parametro \(\phi\) della Bernoulli come un Beta in quanto sappiamo dalla lezione 04 che la Beta è la coniugata della Bernoulli.
In pratica la model selection viene effettuata nell'ambito di un processo chiamato validation process.
Il validation process può essere svolto principalmente in due modi diversi:
L'idea è quella di dividere il dataset in due insiemi: il training set, utilizzato per imparare, e il test set, utilizzato per misurare la qualità del modello. Questo approccio offre dei buoni risultati quando si hanno un numero significativo di dati, in modo da garantire che sia il training set che il test set abbiano delle buone dimensioni.
L'idea in questo caso è quella di dividere il dataset in \(K\) sottoinsiemi della stessa dimensione (\(K\) fold cross validation). Iterativamente poi, in \(K\) fasi, si utilizza ciascun sottoinsieme come test set e l'unione degli altri \(K-1\) sottoinsiemi come training set. Alla fine abbiamo \(K\) valutazioni diverse, e possiamo prendere come valutazione finale la media delle valutazioni.
Un caso particolare della cross-validation prende il nome di leave-one-out cross validation e consiste nel togliere in modo iterativo un elemento e nell'utilizzare tutti gli altri punti come training set.
Rispetto ai processi di validazione, che tendenzialmente sono molto costosi, è possibile utilizzare delle misure riprese dalla teoria delle informazioni. Queste misure permettono di misurare la qualità di un modello. Tra queste misure troviamo:
Sia \(\mathbf{\Theta})\) l'insieme dei parametri del modello, e sia \(\theta_{\text{ML}}\) il valore ottenuto applicando la stima di massima verosomiglianza al dataset \(\mathbf{X}\). Alora otteniamo
\[\text{AIC} = 2| \theta | - 2 \log P(\mathbf{X} | \theta_{\text{ML}}) = 2| \theta | - 2\underset{\theta}{\max} l(\theta | \mathbf{X})\]
Il modello da individuare in termine di complessità è quindi il modello che ha un \(\theta\) che minimizza questa espressione.
Il BIC è una variante del precedente ed è così definito
\[\text{BIC} = | \theta | \log{|\mathbf{X}|} - 2 \log P(\mathbf{X} | \theta_{\text{ML}}) = | \theta | \log{|\mathbf{X}|} - 2\underset{\theta}{\max} l(\theta | \mathbf{X})\]
L'unica cosa che cambia è il modo in cui si misura la complessità del modello.