ML - 07 - Fitting of Polynomial II
Date:
Lecturer: Giorgio Gambosi
Slides: ()
In questa lezione abbiamo trattato il problema del fitting di un polinomio, questa volta però utilizzando un modello probabilistico.
Come abbiamo già visto, lo schema di riferimento nell'apprendimento supervisionato deterministico è composto dai seguenti elementi
Un algoritmo di previsione \(h(\cdot)\) che, dato i valori delle features di un certo punto \(x_i\), ci fornisce il valore predetto \(h(x_i) = y_i\)
Un training set \(T(X, T)\), ovvero un insieme di punti \((x_i, t_i)\).
Una funzione di costo \(C\) che ci fornisce una misura del costo associato al fatto di prevedere \(y_i\) invece del valore corretto \(t_i\).
L'idea è quindi quella di cercare la funzione \(h(\cdot)\) all'interno di una famiglia di funzioni \(H\) tale che la funzione di costo \(C(y_i, t_i)\) è la più piccola possibile.
In ambito probabilistico si cerca di fare la stessa cosa, ovvero si cerca di ottimizzare una grandezza che è funzione sia del modello di previsione che stiamo utilizzando e sia dei dati del training set.
Ad ogni particolare funzione di previsione \(h(\cdot)\) associamo una distribuzione di probabilità \(P_h(y|x)\) dipendente da tale funzione. Così facendo quindi per ogni valore del training set \(x\) abbiamo tramite \(P_h(y|x)\) siamo in grado di descrivere la probabilità dei possibili valori predetti associati ad \(x\).
Per ottenere poi la quantità da ottimizzare mi calcolo per ogni coppia \((x_i, t_i)\) del training set la probabilità di predirre il punto \(t_i\) utilizzando il modello \(h(\cdot)\), ovvero il valore \(P_h(t_i|x)\), e moltiplico queste probabilità tra loro per ottenere
\[L(h) = P_h(t_1 | x_1) \cdot P_h(t_2 | x_2) \cdot \ldots \cdot P_h(t_n | x_n)\]
Notiamo che fissato un training set il valore di \(L\) è solo funzione di \(h\). L'idea è quindi quella di trovare il valore di \(h\) tale per cui \(L(h)\) sia il più grande possibile. In altre parole, stiamo massimizzando la verosomiglianza, in quanto stiamo cercando la funzione \(h(\cdot)\) che mi rende più probabile generare i valori target \(t_i\) a parte dai valori \(x_i\).
Supponiamo quindi di avere un certo insieme di elementi (pallini blu), e supponiamo di considerare una particolare funzione di predizione \(y(x, \mathbf{w})\).
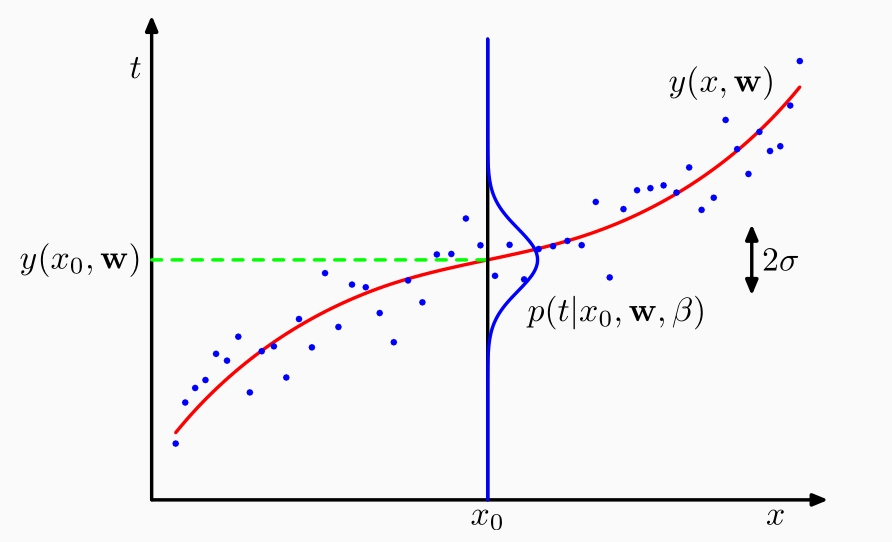
A questo punto definiamo un modello in cui la distribuzione \(P_h(y_i | x_i)\) è una distribuzione normale di media \(h(x_i)\) e di varianza \(\sigma^2 = \beta^{-1}\).
Una volta definito questo modello ci possiamo chiedere qual'è la probabilità di generare \(t_i\) per ogni valore \(x_i\) del training set utilizzando la distribuzione \(P_h(y_i | x_i)\).
È possibile poi stimare il parametro \(\beta_{\text{ML}}\) e i coefficienti del polinomio \(\mathbf{w}_{\text{ML}}\) andando a trovare i valori che massimizzano la likelihood (o equivalentemente il suo logaritmo).
\[L(t | X, w, \beta) = P(t|X, w, \beta) = \prod_{i = 1}^n \mathcal{N}(t_i | y(x_i, w), \beta^{-1})\]
dove il suo logaritmo è pari a
\[\begin{split} l(t | X, w, \beta) &= \sum_{i = 1}^n \log{\mathcal{N}(t_i | y(x_i, w), \beta^{-1})} \\ &= \sum_{i = 1}^n \log{\Big(\frac{\sqrt{\beta}}{\sqrt{2 \pi}} e^{-\frac{\beta}{2}(t_i - y(x_i, w))^2} \Big)} \\ &= -\sum_{i = 1}^n \frac{\beta}{2}(t_i - y(x_i, w))^2 + \frac{n}{2}\log \beta - \frac{n}{2} \log{2 \pi} \\ &= -\frac{\beta}{2} \sum_{i = 1}^n (t_i - y(x_i, w))^2 + \frac{n}{2}\log{\beta} + C \\ \end{split}\]
dove \(C\) è una costante.
Notiamo che massimizzare \(l(t|X,w, \beta)\) rispetto a \(w\) equivale a minimizzare la seguente espressione
\[\frac{1}{2} \sum_{i = 1}^n (t_i - y(x_i, w))^2\]
che è proprio la somma dei quadrati che abbiamo già incontrato.
Observation: anche se il risultato finale è lo stesso che avevo già ottenuto, adesso però abbiamo un modello più completo, che ci permette di vedere che questa particolare scelta di funzione da minimizzare è motivata da considerazioni di tipo probabilistico.
Se invece vogliamo massimizzare \(l(t|X,w, \beta)\) rispetto alla precisione \(\beta\) allora dobbiamo settare a \(0\) la seguente derivata
\[\frac{\partial l(t|X,w,\beta)}{\partial \beta} = -\frac{1}{2}\sum\limits_{i = 1}^n (t_i - y(x_i, w))^2 + \frac{n}{2\beta}\]
che una volta risolta ci permette di ottenere
\[\beta^{-1}_{\text{ML}} = \frac{1}{n} \sum\limits_{i = 1}^n (t_i - y(x-i, w))^2\]
Utilizzando questi parametri siamo quindi in grado di effettuare le previsioni come segue
\[P(t | x, w, \beta) = \mathcal{N}(t | y(x, w), \beta^{-1}) = \sqrt{\frac{\beta_{\text{ML}}}{2 \pi}}e^{-\frac{\beta_{\text{ML}}}{2} (t - y(x, w_{\text{ML}}))^2}\]
Se invece vogliamo approcciare le cose con un punto di vista bayesiano, allora al posto di stimare particolari valori per i parametri \(\beta\) e \(W\) possiamo assumere inizialmente che i parametri \(\beta\) e \(W\) siano distribuiti secondo una gaussiana.
In particolare quindi assumiamo che i coefficienti \(w\) siano distribuiti con una gaussiana multivariata a media \(0\) e con una matrice di covarianza diagonale con valori degli elementi tutti uguali all'inverso di un iperparametro \(\alpha\).
\[P(w|\alpha) = \mathcal{N}(w|0, \alpha^{-1}I) = \Big(\frac{\alpha}{2\pi}\Big)^{\frac{M+1}{2}} e^{-\frac{\alpha}{2}w^Tw}\]
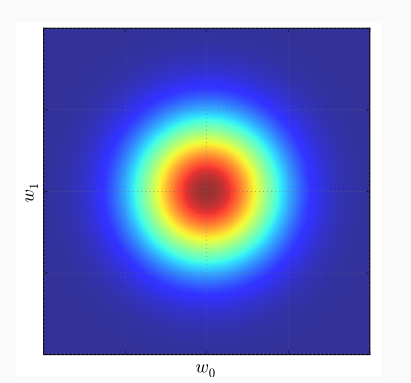
Applicando la regola di Bayes otteniamo quindi
\[P(w|X, t; \alpha, \beta) \propto P(t|X, w; \beta) P(w|\alpha)\]
ed effettuando l'inferenza via MAP otteniamo che il valore di W che massimizza la probabilità a posteriori minimizza anche la seguente espressione
\[\frac{\beta}{2} \sum\limits_{i = 1}^n (t_i - y(x_i, w))^2 + \frac{\alpha}{2}W^t W = \beta \Bigg( \frac{1}{2} \sum\limits_{i = 1}^n (t_i - y(x_i, w))^2 + \frac{\alpha}{2\beta}||w||^2 \Bigg)\]
Come è possibile vedere quindi il rapporto \(\alpha/\beta\) rappresenta l'iperparametro di regolarizzazione.
In questo caso la distribuzione di predizione di \(t\) dato \(x\) è analoga a quella trovata applicando il metodo ML, solo che questa volta abbiamo i parametri stimati tramite la MAP.
\[P(t | x, w, \beta) = \mathcal{N}(t | y(x, w), \beta^{-1}) = \sqrt{\frac{\beta_{\text{MAP}}}{2 \pi}}e^{-\frac{\beta_{\text{MAP}}}{2} (t - y(x, w_{\text{MAP}}))^2}\]
È possibile poi dimostrare che
\[\beta_{\text{MAP}} =\beta_{\text{ML}}\]
In un ambito puramente bayesiano la predizione non è fatta selezionando uno dei possibili modelli (ovvero assumendo di utilizzare un polinomio), ma si cerca di comporre le predizioni che possono essere effettuate da tutti i possibili modelli.
In particolare si ha che
\[\begin{split} P(t|x;X, t) &= \int P(t, w| x; X, t) \,\, dw \\ &= P(t|w,x;X,t) P(w|x;X,t) \,\, dw \\ &= P(t|w,x) P(w|X, t) \,\, dw \\ \end{split}\]
Infatti,
\(w\) è indipendente da \(x\), ma dipende solo dal training set, e quindi
\[P(w|x;X,t) = P(w|X,t)\]
Una volta fissato \(w\), \(t\) è indipendente dal trianing set, e quindi
\[P(t|w,x;X,t) = P(t|w,x)\]
Nell'ipotesi in cui tutte le seguenti quantità sono gaussiane
\[\begin{split} P(t|w,x;\beta) \\ P(w;\alpha) \\ P(t|w,X) \\ \end{split}\]
abbiamo che anche la probabilità finale è gaussiana
\[P(t|x, X, t) = \mathcal{N}(t|m(x), s^2(x))\]
con media e varianza ottenute dal training set come segue
\[\begin{split} m(x) &= \beta x^T S \sum_{i = 1}^n x_i t_i \\ \\ s^2(x) &= \beta^{-1} + x^T S x \\ \\ S &= \alpha I + \beta \sum_{i = 1}^n x x^T \\ \end{split}\]
A differenza dei casi precedenti, in questo caso fissato un valore di \(x\) non solo possiamo calcolare la media, ma possiamo anche calcolare la varianza, che sarà in funzione di \(x\).
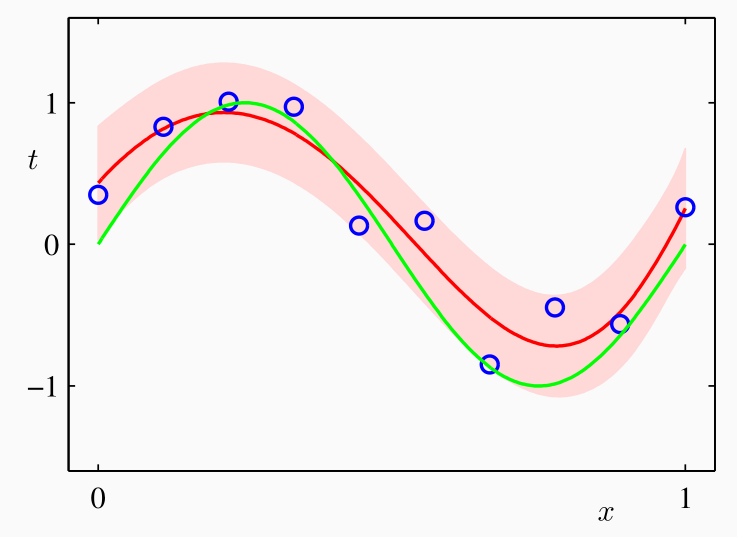
Il modello risultante quindi è sia più complesso che più potente, in quanto ci permette di stimare l'incertezza del risultato in funzione del punto che si vuole stimare. Tipicamente più questo punto si allontana dal training set e maggiore sarà l'incertezza associata al punto.