ML - 09 - Linear Classification I
Date:
Lecturer: Giorgio Gambosi
Slides: (ml_05_linclass-slides.pdf)
Table of contents:
In questa lezione abbiamo introdotto le basi della classificazione lineare.
A differenza della regressione, in cui il valore da associare all'elemento \(x\) è preso da un insieme di dimensione continua, come ad esempio \(\mathbb{R}\), nella classificazione i valori \(t\) da predirre sono presi da un insieme discreto, dove ciascun valore denota una particolare classe.
Esempi: Dato un insieme di clienti dei tipici problemi di classificazione sono:
Predirre se il cliente è sano o malato.
Predirre se il cliente è interessante o no.
Il caso più comune quando si tratta la classificazione è caratterizzato dal fatto che ogni elemento elemento da classificare appartiene ad una e una sola classe. In una situazione di questo tipo è possibile vedere geometricamente lo spazio di input come partizionato in una serie di decision regions (regioni di decisione). Le dimensioni dello spazio di input dipendono dal numero delle features associate ad ogni elemento da classificare. Tutti i punti che fanno parte della stessa regione sono assegnati alla stessa classe.
Nel caso in cui abbiamo un modello di classificazione lineare, i decision boundaries, ovvero i confini che definiscono le decision regions, sono funzioni lineari rispetto all'input \(x\).
Un dataset in questo caso contiene un insieme di elementi con i relativi valori delle features, e per ogni elemento il relativo valore target, ovvero la classe a cui quell'elemento appartiene. Visivamente è possibile utilizzare un colore diverso per distinguere gli elementi delle varie classi.
Se è possibile separare le varie classi (insieme di punti) di un dataset in modo chiaro tramite dei confini lineari (linear decision boundaries), allora le classi del dataset sono dette linearly separable (separabili linearmente).
Nella regressione il valore target \(\mathbf{t}\) è un vettore di reali. Nella classificazione invece ci sono vari modi per rappresentare le classi:
Binary classification: Viene utilizzata una variabile \(t \in \{0, 1\}\), dove \(t = 0\) denota la classe \(C_0\) e \(t = 1\) denota la classe \(C_1\).
More than 2 classes: Si utilizza codifica "1 of \(K\)" (detta anche one-hot encoding) in cui per rappresentare la classe \(C_j\) si utilizza un vettore \(\mathbf{t}\) di \(K\) bits in cui tutti i bit sono \(0\) tranne il \(j\) esimo, che è \(1\).
In generale ci sono tre approcci diversi alla classificazione lineare, uno deterministico e due probabilistici:
Discriminant function: Si cerca una funzione \(f: \mathbf{X} \to \{1, \ldots, K\}\), detta discriminant function, che mappa ogni input \(x\) ad una classe \(C_i\) tale che \(i = f(x)\).
Discriminative approach: Si determina la probabilità condizionata \(P(C_j|x)\) in una fase iniziale detta inference phase, e si utilizza tale distribuzione in una seconda fase, detta decision phase, per assegnare all'input una determinata classe.
Generative approach: Si determina la probabilità condizionata alla classe \(P(X|C_j)\) e la prior probability della classe \(P(C_j)\), e si applica la regola di Bayes per ottenere la probabilità a posteriori della classe \(P(C_j|x)\). Queste distribuzioni a posteriori vengono poi utilizzate per assegnare una classe ad ogni input.
I due approcci probabilistici differiscono in quanto nell'approccio discriminativo si inferiscono direttamente le probabilità \(P(C_j|x)\), mentre nell'approccio generativo si calcolano tali probabilità partendo da \(P(x|C_j)\) e \(P(C_j)\) e applicando la regola di Bayes.
Observation: \(P(x|C_j)\) è la probabilità che \(x\) appartiene alla classe \(C_j\), ovvero è la distribuzione di probabilità degli elementi appartenenti alla classe \(C_j\).
I primi due approcci invece sono detti discriminative in quanto affrontano il problema della classificazione derivando, a partire dal trianing set, un insieme di condizioni (ad esempio i decision boundaries) che, applicati ad un determinato input, permettono di discriminare la classe da associare a quell'input da tutte le altre.
Il terzo approccio invece è detto generativo e costruisce, a partire dal training set, un modello per ogni classe. In particolare quindi permette la generazione casuale di nuovi elementi per ogni classe da classificare. Paragonando l'elemento da classificare rispetto tutti i modelli, è possibile trovare il modello che descrive meglio l'elemento, e assegnare l'elemento alla classe associata a tale modello.
Un concetto tipicamente utilizzato nella classificazione lineare è l'idea di modello lineare generalizzato (generalized linear model).
Ricordiamo che nell'ambito della regressione lineare, la predizione del modello viene espressa tramite una funzione lineare
\[y(\mathbf{x}) = \mathbf{w}^T \mathbf{x} + w_0\]
Invece, nell'ambito della classificazione, per avere un modello the ci permette di ottenere le probabilità delle varie classi si utilizza un modello lineare generalizzato
\[y(\mathbf{x}) = f(\mathbf{w}^T \mathbf{x} + w_0)\]
dove \(f(\cdot)\) è una funzione non lineare detta activation function.
In questo caso le superfici di separazione (boundaries) corrispondono alle soluzioni di \(y(\mathbf{x}) = c\) per qualche costante \(c\). Questo ci permette di ottenre che
\[\mathbf{w}^T \mathbf{x} + w_0 = f^{-1}(c)\]
è un linear boundary. La funzione inversa \(f^{-1}\) è detta link function.
Consideriamo un problema di classificazione binaria, e quindi di utilizzare funzioni discriminative lineari. In questo caso abbiamo che la superficie dell'iperpiano di separazione è \(D-1\) dimensionale e suddivide le regioni delle due classi tramite una certa equazione lineare della forma
\[y(\mathbf{x}) = \mathbf{w}^T \mathbf{x} + w_0 = 0\]
Dati due punti dell'iperpiano \(\mathbf{x}_1, \mathbf{x}_2\), abbiamo che
\[\begin{split} &y(\mathbf{x}_1) = y(\mathbf{x}_2) = 0 \\ \iff \,\,\,\, & \mathbf{w}^t(\mathbf{x}_1) - \mathbf{w}^t(\mathbf{x}_1) = \mathbf{w}^T(\mathbf{x}_1 - \mathbf{x}_2) = 0 \\ \end{split}\]
e quindi \(\mathbf{x}_1 - \mathbf{x}_2\) e \(\mathbf{w}\) sono ortogonali. Questo ci dice che il vettore dei coefficienti di un iperpiano è ortogonale all'iperpiano stesso.
Per un qualcunque elemento su questo iperpiano \(\mathbf{x}\), ovvero t.c. \(y(\mathbf{x}) = 0\), il valore \(\mathbf{w}^T \mathbf{x}\) è, per definizione, la lunghezza della proiezione di \(\mathbf{x}\) nella direzione di \(\mathbf{w}\) calcolato in multipli di \(||\mathbf{w}||_2\).
Se poi normalizziamo rispetto alla norma \(||\mathbf{w}||_2 = \sqrt{\sum_i w_i^2}\) otteniamo la lunghezza della proiezione di \(\mathbf{x}\) nella direzione ortogonale all'iperpiano, assumendo \(||\mathbf{w}||_2 = 1\).
Infine, dato che \(\mathbf{w}^T \mathbf{x} = -w_0\), abbiamo che
\[\frac{\mathbf{w}^T \mathbf{x}}{||w||} = -\frac{w_0}{||w||}\]
e quindi la distanza dall'iperpiano è determinata dal valore di treshold \(w_0\).
Questo significa che per un qualunque punto \(\mathbf{x}\), il valore \(y(\mathbf{x}) = \mathbf{w}^T \mathbf{x} + w_0\) ci fornisce la distanza (in multipli di \(||w||\)) dell'elemento \(x\) dall'iperpiano.
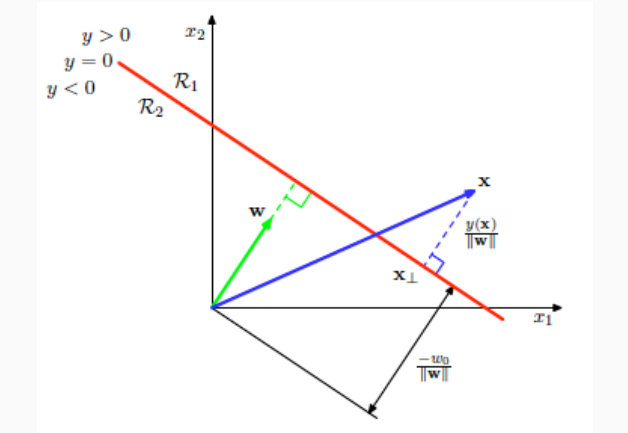
Andando a stimare il valore \(y(\mathbf{x})\), posso capire sia la distanza del punto dall'iperpiano (utilizzando il valore assoluto), e sia da che parte mi trovo dell'iperpiano (utilizzando il segno), ovvero in quale classe sto.
Observation: La distanza di un punto dall'iperpiano di separazione può essere interpretata come la "confidenza" che abbiamo nell'attribuire al punto una determinata classe: più il punto è distanza, e più siamo sicuri della nostra classificazione.
Consideriamo adesso un problema di classificazione in cui abbiamo \(K\) classi da classificare.
Un primo approccio potrebbe essere quello di definire \(K-1\) funzioni di discriminazione, e la funzione \(f_i\) viene utilizzata per discriminare i punti appartenenti alla classe \(C_i\) dai punti che appartengono a tutte le altri classi, per \(1 \leq i \leq K - 1\). In particolare,
\[f_i(x) > 0 \implies x \in C_i\]
altrimenti \(x \not \in C_i\).
Questo approccio però presenta delle problematiche. Consideriamo il seguente esempio
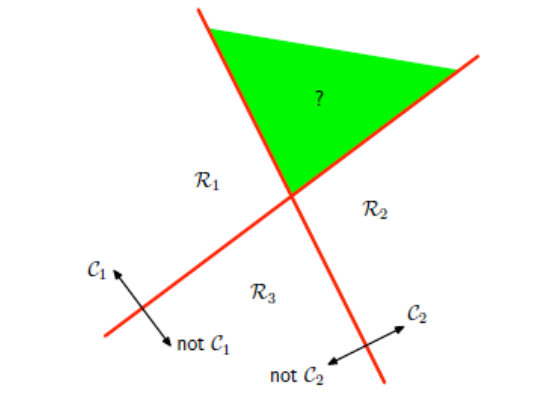
notiamo che i punti appartenenti alla regione verde vengono classificati correttamente sia da \(f_1\) che da \(f_2\), ma questo non può essere, in quanto assumiamo di lavorare con elementi che possono far parte di una e una sola classe.
Come secondo approccio potremmo definire una funzione di discriminazione per ogni coppia di classi.
Così facendo avremmo \(K(K-1)/2\) funzioni, dove la funzione \(f_{i, j}\) ci servirebbe per discriminare i punti che potrebbero appartenere alla classe \(C_i\) dai punti che potrebbero appartenere alla classe \(C_j\). Ciascun elemento sarebbe poi classificato utilizzando una regola di maggioranza.
Anche questo approccio però non funziona, come mostra il seguente esempio, in cui è presenza una zona del piano (la zona verde), in cui non è possibile assegnare in modo univoco una classe ai punti.
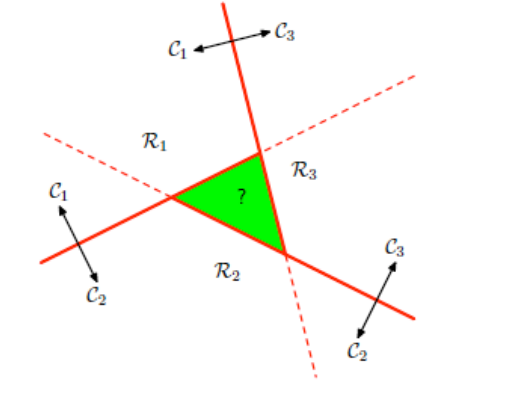
L'approccio effettivamente utilizzato è il seguente: si definiscono \(K\) funzioni lineari
\[y_i(\mathbf{x}) = \mathbf{w}_i^T \mathbf{x} + w_{i, 0}\]
Ogni elemento \(\mathbf{x}\) è assegnato alla classe \(C_k\) se e solo se \(y_k(x) > y_j(x)\) per tutti i \(j \neq k\). Ovvero,
\[k = \underset{j}{\text{argmax}} \,\,\, y_j(\mathbf{x})\]
Fissate due classi \(C_i\) e \(C_j\), il decision boundary tra le due classi è definito da tutti i punti \(\mathbf{x}\) tali che \(y_i(\mathbf{x}) = y_j(\mathbf{x})\), ovvero dal seguente \(D-1\) dimensional hyperplane
\[(\mathbf{w}_i - \mathbf{w}_j)^T \mathbf{x} + (w_{i,0} - w_{j, 0}) = 0\]
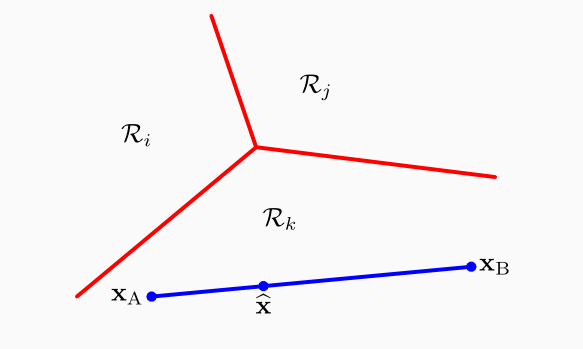
Observation: È poi possibile dimostrare che le regioni di decisioni risultanti da questo procedimento sono connesse e convesse, ovvero possiamo muoveris da un punto ad un altro di ogni classe senza uscire dalla regione per quella classe, e se consideriamo il segmento che unisce i due punti, tutti i punti del segmento fanno parte della regione.
Notiamo che quanto trattato per le funzioni discriminanti lineari può essere generalizzato. Ad esempio possiamo lavorare con delle quadratic discriminant functions, definite come segue
\[y(\mathbf{x}) = w_0 + \sum\limits_{i = 1}^D w_i x_i + \sum\limits_{i = 1}^D \sum\limits_{j = 1}^i w_{i, j} x_i x_j\]
In questo caso ovviamente i decision boundaries saranno più complessi rispetto a quanto visto nel caso di funzioni discriminanti lineari.
In generale, possiamo avere delle generalized discriminant functions utilizzando un insieme di funzioni \(\phi_1, \ldots, \phi_m\) come segue
\[y(\mathbf{x}) = w_0 + \sum\limits_{i = 1}^M w_i \phi_i(\mathbf{x})\]