ML - 10 - Linear Classification II
Date:
Lecturer: Giorgio Gambosi
Slides: (ml_05_linclass-slides.pdf)
Table of contents:
In questa lezione abbiamo visto tre metodi per risolvere la classificazione lineare:
Tramite regressione.
Tramite il discriminante lineare di Fisher.
Tramite il percettrone.
Il primo approccio alla classificazione che vediamo è basato sull'adattare la regressione lineare che abbiamo già visto a questo nuovo problema.
Assumiamo di avere \(K\) classi, e rappresentiamo le classi con un one-hot-encoding tramite un insieme di variabili \(z_1, \ldots, z_k\), dove la classe \(C_i\) è codificata dal vettore con valori \(z_i = 1\) e \(z_k = 0\) per \(k \neq i\).
Il nostro target è quindi formato da una matrice in cui ad ogni elemento, ovvero ad ogni riga della matrice, corrisponde un vettore che rappresenta una particolare classe.
Consideriamo poi la colonna \(i\) della matrice, e poniamoci il problema di inferire, a partire dai valori delle features, il valore della variabile \(z_i\). Anche se \(z_i\) è una variabile che assume valore in un insieme discreto, ignoriamo questo dettaglio e utilizziamo quanto visto per la regressione per trovare delle funzioni discriminanti \(y_i(\mathbf{x}) = \mathbf{w}_i^T + w_{i,0}\).
Una volta fatto questo l'elemento \(\mathbf{x}\) è associato alla classe \(C_k\) tale che
\[K = \underset{i}{\text{argmax }} y_i(\mathbf{x})\]
e quindi \(z_k(\mathbf{x}) = 1\) e \(z_j(\mathbf{x}) = 0\) per ogni \(j \neq k\).
I parametri di tutti i modelli lineari ottenuti per regressione possono poi essere raggruppati in una singola matrice
\[\mathbf{y}(\mathbf{x}) = \mathbf{W}^T \overline{\mathbf{x}}\]
Observation: Quando scriviamo \(\overline{\mathbf{x}}\) intendiamo il vettore delle features di \(\mathbf{x}\) esteso con una componente aggiuntiva che assume sempre il valore \(1\).
In generale una funzione di regressione fornisce una stima del target \(t\) dato l'input \(x\). In realtà, dato che potrei avere valori di target diversi per lo stesso punto, quello che viene effettivamente stimato è il valore \(\mathbb{E}[t|x]\), ovvero il valore atteso del target dato l'input.
Questo significa che in particolare la funzione \(y_i(\mathbf{x})\) è una funzione di regressione rispetto alla variabile \(z_i\), e quindi può essere considerata come una stima del valore attesso della v.a. binaria \(z_i\) condizionato all'aver visto \(x\), ovvero \(\mathbb{E}[z_i|x]\).
Se assumiamo che \(z_i\) è distribuita secondo una distribuzione di Bernoulli, tale valore atteso corrisponde alla posterior probability. E dato che \(y_i(\mathbf{x})\) stima \(\mathbb{E}[z_i|x]\) otteniamo
\[\begin{split} y_i(\mathbf{x}) &\approx \mathbb{E}[z_i|x] \\ &= P(z_i = 1 | \mathbf{x}) \cdot 1 + P(z_i = 0 | \mathbf{x}) \cdot 0 \\ &= P(z_i = 1 | \mathbf{x}) \\ &= P(C_i | \mathbf{x}) \\ \end{split}\]
Possiamo quindi vedere come \(y_i(\mathbf{x})\) ci permette di stimare la probabilità che interessa a noi per effettuare la classificazione. In ogni caso, è importante sottolineare il fatto che \(y_i(\mathbf{x})\) non è un valore di probabilità, in quanto potrebbe assumere un valore al di fuori dell'intervallo \([0,1]\).
Vediamo adesso come apprendere il valore dei coefficienti di questi \(K\) modelli lineari partendo dal nostro training set \(\mathbf{X}, \mathbf{t}\).
Un elemento del training set è una coppia \((\mathbf{x}_i, \mathbf{t}_i)\), dove \(\mathbf{x}_i \in \mathbb{R}^D\) e \(\mathbf{t}_i \in \{0, 1\}^K\).
La matrice dei coefficienti \(\mathbf{W} \in \mathbb{R}^{(D+1) \times K}\) contiene tutti i parametri delle funzioni \(y_i\) ottenuti tramite least squares (regressione lineare). In particolare la colonna \(i\) esima rappresenta i \(D+1\) parametri \(w_{i,0}, \ldots, w_{i,D}\) della funzione \(y_i\).
\[\mathbf{W} = \begin{pmatrix} w_{1,0} & w_{2,0} & \ldots & w_{K,0} \\ w_{1,1} & w_{2,1} & \ldots & w_{K,1} \\ \vdots & \vdots & \ddots & \vdots \\ w_{1,D} & w_{2,D} & \ldots & w_{K,D} \\ \end{pmatrix}\]
posso riassumere il vettore dei valori stimati nel seguente modo
\[\mathbf{y}(\mathbf{x}) = \mathbf{W}^T \overline{\mathbf{x}}\]
con \(\overline{\mathbf{x}} = (1, x_1, \ldots, x_{D-1}, x_D)\)
Continuando, posso rappresentare l'intero insieme degli elementi del training set tramite una matrice \(\overline{\mathbf{X}} \in \mathbb{R}^{n \times (D+1)}\) in cui ogni colonna corrisponde ad ogni feature, e ogni riga ad ogni elemento.
\[\overline{\mathbf{X}} = \begin{pmatrix} 1 & x_1^{(1)} & \ldots & x_1^{(D)} \\ 1 & x_2^{(1)} & \ldots & x_2^{(D)} \\ \vdots & \vdots & \ddots & \vdots \\ 1 & x_n^{(1)} & \ldots & x_n^{(D)} \\ \end{pmatrix}\]
Effettuando il prodotto tra la matrice \(\overline{\mathbf{X}}\) e la matrice \(\mathbf{W}\), ottengo una matrice di size \(n \times K\) che rappresenta le predizioni di ogni funzione lineare \(y_j\) per ogni elemento del training set. In particolare,
\[(\overline{\mathbf{X}} \mathbf{W})_{i,j} = w_{j,0} + \sum\limits_{k = 1}^D x_i^{(k)} w_{j,k} = y_j(\mathbf{x}_i)\]
Per capire la bontà del modello ottenuto confrontiamo il valore \(y_j(\mathbf{x}_i)\) con l'elemento \(\mathbf{T}_{i,j}\) nella matrice \(\mathbf{T}\), che è una matrice di size \(n \times K\) in cui la riga \(i\) esima corrisponde alla codifica 1-of-K nella classe associata all'elemento \(x_i\).
In particolare quindi considero la matrice dei residui
\[(\overline{\mathbf{X}} \mathbf{W} - \mathbf{T})_{i,j} = y_j(\mathbf{x}_i) - t_{i,j}\]
Posso poi calcolare la matrice
\[(\overline{\mathbf{X}} \mathbf{W} - \mathbf{T})^T (\overline{\mathbf{X}} \mathbf{W} - \mathbf{T})\]
e se considero gli elementi nella sua diagonale, ottengo
\[\Big((\overline{\mathbf{X}} \mathbf{W} - \mathbf{T})^T (\overline{\mathbf{X}} \mathbf{W} - \mathbf{T})\Big)_{i,i} = \sum\limits_{j = 1}^K \Big(y_j(\mathbf{x}_i) - t_{i,j}\Big)^2\]
Quindi, assumendo ceh \(x_i\) si trova nella classe \(C_k\), otteniamo
\[\Big((\overline{\mathbf{X}} \mathbf{W} - \mathbf{T})^T (\overline{\mathbf{X}} \mathbf{W} - \mathbf{T})\Big)_{i,i} = (y_k(x_i) - 1)^2 + \sum\limits_{j \neq k} y_j(\mathbf{x}_i)^2\]
Per avere una misura rispetto all'intero training set dobbiamo sommare gli elementi nella diagonale di \((\overline{\mathbf{X}} \mathbf{W} - \mathbf{T})^T (\overline{\mathbf{X}} \mathbf{W} - \mathbf{T})\). Tale somma equivale proprio alal somma dei quadrati delle differenze tra il valore predetto dal modello \(\mathbf{W}\) e il valore effettivo. Questa somma corrisponde alla traccia della matrice \((\overline{\mathbf{X}} \mathbf{W} - \mathbf{T})^T (\overline{\mathbf{X}} \mathbf{W} - \mathbf{T})\).
Il nostro obiettivo è quindi quello di minimizzare la seguente quantità
\[E(\mathbf{W}) = \frac12 \cdot \text{tr}\Big((\overline{\mathbf{X}} \mathbf{W} - \mathbf{T})^T (\overline{\mathbf{X}} \mathbf{W} - \mathbf{T})\Big)\]
Come al solito, procediamo risolvendo
\[\frac{\partial E(\mathbf{W})}{\partial \mathbf{W})} = 0\]
Per risolvere tale equazione cominciamo notando che è possibile esprimere il gradiante di \(E(\mathbf{W})\) nel seguente modo
\[\frac{\partial E(\mathbf{W})}{\partial \mathbf{W})} = \overline{\mathbf{X}}^T \overline{\mathbf{X}} \mathbf{W} - \overline{\mathbf{X}}^T \mathbf{T}\]
Impostando il lato destro della precedente equzione a \(\mathbf{0}\), otteniamo
\[\mathbf{W} = (\overline{\mathbf{X}}^T \overline{\mathbf{X}})^{-1} \overline{\mathbf{X}}^T \mathbf{T}\]
e quindi l'insieme delle funzioni discriminanti ci è dato da
\[\mathbf{y}(\mathbf{x}) = \mathbf{W}^T \overline{\mathbf{x}} = \mathbf{T}^T \overline{\mathbf{X}}(\overline{\mathbf{X}}^T \overline{\mathbf{X}})^{-1} \overline{\mathbf{x}}\]
Il metodo che abbiamo appena visto è un metodo alquanto semplice di apprendimento, in quanto può essere fatto tramite l'utilizzo di una forma chiusa (closed form).
Questo metodo è poi molto sensibili agli outliers, ovvero agli elementi che rispetto alle classi in gioco si pongono in modo eccentrico.
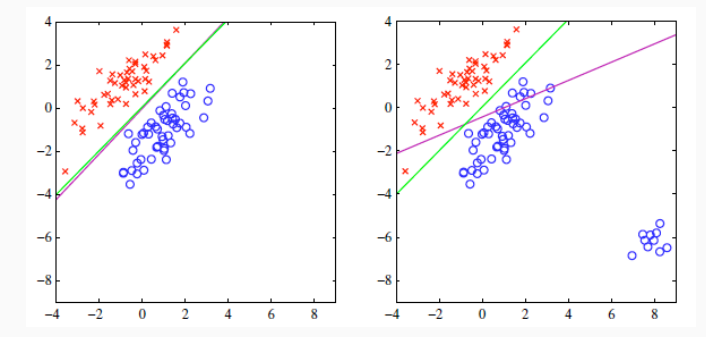
Il metodo tende anche ad avere una poca precisione nei casi in cui abbiamo più di due classi \(K > 2\).
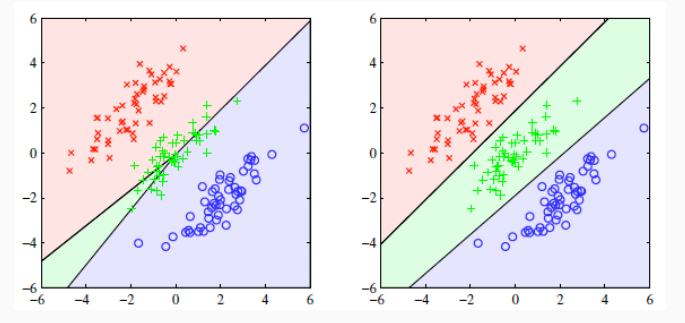
Il metodo del discriminante lineare di Fisher (Fisher linear discriminant) è un metodo algebrico che può essere utilizzato per effettuare classificazione binaria, ma che permette anche delle estensioni al caso multiclasse. In questa sede considereremo solamente il caso binario.
Il discriminante lineare di Fisher si basa sulla Linear Discriminant Analysis (LDA) è quella di trovare una proiezione lineare del training set in un opportuno sottospazio in modo tale da separare il più possibile i punti delle varie classi.
Observation: Il termine LDA presenta delle ambiguità, in quanto può anche essere utilizzato per indicare un approccio generativo che noi però chiameremo Gaussian Discriminant Analysis (GDA).
Graficamente possiamo visualizzare la questione nel seguente modo: consideriamo dei punti nello spazio, il cui colore indica la classe di appartenenza.
A questo punto cerchiamo una retta le cui proiezioni dei punti sulla retta permettano di distinguere in modo chiaro le due classi. Notiamo che non tutte le rette hanno questa caratteristica. Alcune infatti presenteranno una buona separazione delle due classi, mentre altre una separazione quasi nulla.
L'idea è quindi quella di proiettare tutti i punti dello spazio \(D\) dimensionale del training set in uno spazio unidimensionale tramite una trasformazione lineare della forma
\[y = \mathbf{w} \cdot \mathbf{x} = \mathbf{w}^T \mathbf{x}\]
where \(\mathbf{w}\) è il vettore \(D\) dimensionale che corrisponde alla direzione della proiezione desiderata, e dato che ci sono più vettori \(D\) dimensionali che corrispondo alla direzione della proiezione, noi consideriamo solamente quello a norma unitaria.
Se \(K = 2\) si deriva un velore di threshold \(\tilde{y}\) e si assegna un elemento \(\mathbf{x}\) alla classe \(C_1\) se e solo se la sua proiezione \(y = \mathbf{w}^T \mathbf{x}\) è tale che \(y > \tilde{y}\). Altrimenti \(\mathbf{x}\) è assegnato alla classe \(C_2\).
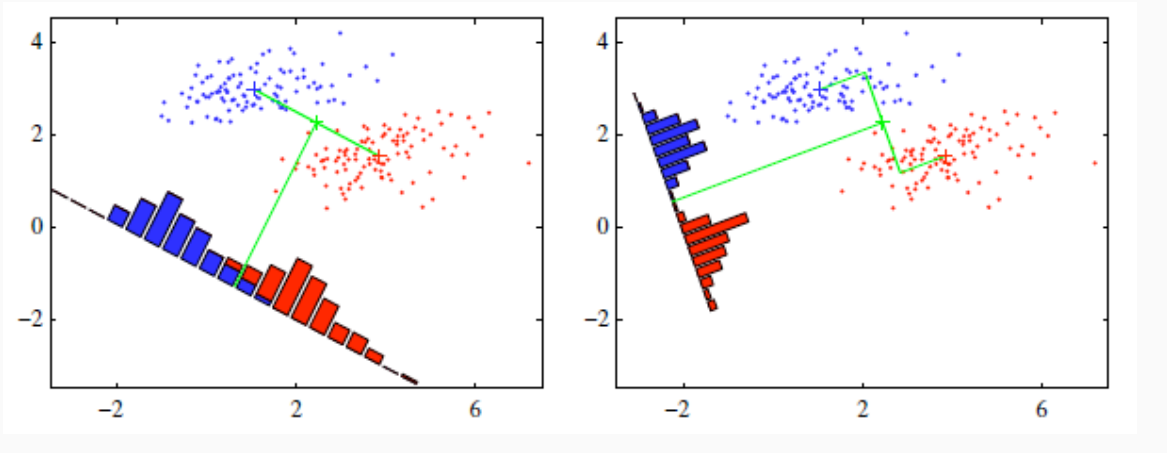
Notiamo che più è netta tale separazione e più il valore soglia ci permetterà di discriminare correttamente la classe di appartenenza di ogni elemento basandoci solamente sulla proiezione dell'elemento calcolata.
Al variare della direzione della proiezione, ovvero al variare dei parametri di \(\mathbf{w}\), si avranno diverse proprietà di separazione.
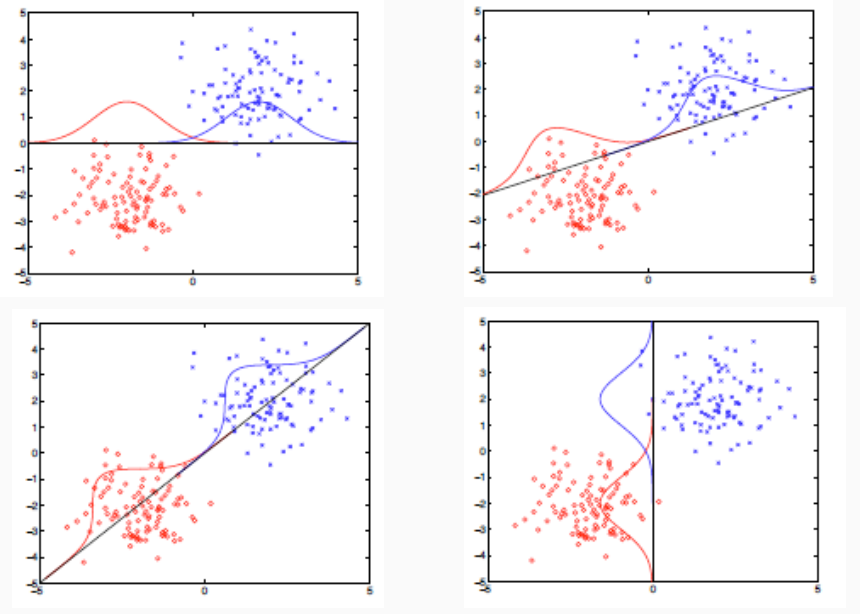
A questo punto per procedere prima definiamo meglio cosa intendiamo quando parliamo di "separabilità" tra due classi. Poi invece procederemo vedendo come effettivamente si calcola tale proiezione.
Supponiamo di avere una proiezione \(\mathbf{w}\), e sia \(n_1\) il numero degli elementi della classe \(C_1\), e sia \(n_2\) il numero degli elementi nella classe \(C_2\). I punti medi (baricentri) delle due classi sono
\[\begin{split} \mathbf{m}_1 &= \frac{1}{n_1} \sum\limits_{\mathbf{x} \in C_1} \mathbf{x} \\ \\ \mathbf{m}_2 &= \frac{1}{n_2} \sum\limits_{\mathbf{x} \in C_2} \mathbf{x} \\ \end{split}\]
Una semplice misura di separazione tra le due classi quando queste vengono proiettate tramite la proiezione \(\mathbf{w}\) potrebbe quindi essere definita come la differenza tra la proiezione dei baricentri delle due classi. In formula,
\[m_2 - m_1 = \mathbf{w}^T \mathbf{m}_2 - \mathbf{w}^T \mathbf{m}_1 = \mathbf{w}^T (\mathbf{m}_2 - \mathbf{m}_1)\]
dove \(m_1\) è la proiezione di \(\mathbf{m}_1\) e \(m_2\) è la proiezione di \(\mathbf{m}_2\).
Per trovare la direzione della retta \(\mathbf{w}\) l'idea è quella di massimizzare la quantità \(m_2 - m_1\).
Notiamo però che \(\mathbf{w}^T(\mathbf{m}_2 - \mathbf{m}_1)\) può essere reso arbitrariamente grande semplicemente moltiplicando \(\mathbf{w}\) con una costante adeguata, non cambiando così facendo la direzione. Per scalvare questo problema considereremo solamente vettori unitari, ovvero vettori \(\mathbf{w}\) tali che
\[||\mathbf{w}||_2 = \mathbf{w}^T \mathbf{w} = 1\]
Così facendo otteniamo il seguente problema di ottimizzazione vincolato
\[\underset{\mathbf{w}: \mathbf{w}^T \mathbf{w} = 1}{\max} \mathbf{w}^T (\mathbf{m}_2 - \mathbf{m}_1)\]
Questo problema può poi essere trasformato in un problema di ottimizzazione senza vincolo modificando opportunamente la funzione obiettivo. Questa trasformazione ci è offerta dalla teoria dei lagrangian multipliers, e ci permette di trasformare il problema di prima nel seguente equivalente
\[\underset{\mathbf{w} \,\,,\,\, \lambda}{\max} \mathbf{w}^T (\mathbf{m}_2 - \mathbf{m}_1) + \lambda(1 - \mathbf{w}^T \mathbf{w})\]
Per risolvere questo problema quindi procediamo come al solito derivando e impostando a \(0\) il risultato.
Per quanto riguarda \(\mathbf{w}\) otteniamo
\[\frac{\partial }{\partial \mathbf{w}} \Big(\mathbf{w}^T (\mathbf{m}_2 - \mathbf{m}_1) + \lambda(1 - \mathbf{w}^T \mathbf{w}) \Big) = \mathbf{m}_2 - \mathbf{m}_1 + 2 \lambda \mathbf{w}\]
impostando a \(\mathbf{0}\) otteniamo
\[\mathbf{w} = \frac{\mathbf{m}_2 - \mathbf{m}_1}{2 \lambda}\]
Per \(\lambda\) invece troviamo
\[\frac{\partial }{\partial \lambda} \Big(\mathbf{w}^T (\mathbf{m}_2 - \mathbf{m}_1) + \lambda(1 - \mathbf{w}^T \mathbf{w}) \Big) = 1 - \mathbf{w}^T \mathbf{w}\]
utilizando adesso la soluzione trovata prima otteniamo
\[1 - \mathbf{w}^T \mathbf{w} = 1 - \frac{(\mathbf{m}_2 - \mathbf{m}_1)^T (\mathbf{m}_2 - \mathbf{m}_1)}{4 \lambda^2} = 0\]
e quindi \(\lambda\) è dato da
\[\lambda = \frac{\sqrt{(\mathbf{m}_2 - \mathbf{m}_1)^T (\mathbf{m}_2 - \mathbf{m}_1)}}{2} = \frac{||\mathbf{m}_2 - \mathbf{m}_1||_2}{2}\]
Sostituendo il valore di \(\lambda\) nell'espressione ottenuta prima otteniamo quindi
\[\mathbf{w} = \frac{\mathbf{m}_2 - \mathbf{m}_1}{||\mathbf{m}_2 - \mathbf{m}_1||_2}\]
Geometricamente questa soluzione ci dice che la direzione che minimizza la distanza della proiezione tra i punti medi è proprio la direzione del vettore che unisce i due punti medi tra loro.
Questo tipo di soluzione non sempre è ottimale, in quanto non prende minimamente in considerazione come i punti delle classi sono distribuiti, ma considera solamente il punto medio. In altre parole, questo metodo non funziona bene per classi con una elavata varianza.
Cerchiamo adesso di migliorare quanto fatto. In particolare vogliamo scegliere una direzione che garantisce:
I punti medi delle due classi sono separati il più possibile.
Le proiezioni delle classi si disperdono il meno possibile.
In particolare quindi vogliamo massimizzare una funzione che presenta i seguenti comportamenti:
Da un lato è crescente rispetto alla separazione delle classi proiettate (questa separazione può essere calcolata tramite il punto medio)
Dall'altro lato però è decrescente rispetto alla dispersione delle proiezioni dei punti per ogni classe.
In particolare quindi la nostra funzione premia la separazione delle due classi, ma penalizza la dispersione rispetto alle singole classi.
A tale fine introduciamo quindi una nuova misura per calcolare la varianza presente nelal proiezione di una classe (within-class variance). Tale misura è definita come segue
\[s_i^2 = \sum\limits_{\mathbf{x} \in C_i} (\mathbf{w}^T \mathbf{x} - m_i)^2\]
dove la total within-class variance è ottenuta sommando le singole within-class variance
\[s_1^2 + s_2^2\]
Per poi avere una funzione che da un lato rende \(m_2 - m_1\) il più grande possibile, e dall'altro rende \(s_1^2 + s_2^2\) il più piccolo possibile, si definisce il Fisher criterion a partire da una direzioner \(\mathbf{w}\) nel seguente modo
\[J(\mathbf{w}) = \frac{(m_2 - m_1)^2}{s_1^2 + s_2^2}\]
Così facendo abbiamo che \(J(\mathbf{w})\) cresce all'aumentare della separazione delle classi, e decresce all'aumentare della within-class variance.
Siano \(S_1\) e \(S_2\) le within-class covariance matrices, definite come segue
\[S_i = \sum\limits_{\mathbf{x} \in C_i} (\mathbf{x} - \mathbf{m}_i) (\mathbf{x} - \mathbf{m}_i)^T\]
è possibile calcolare la within-class covariance delle proiezioni \(s_1^2\) e \(s_2^2\) a partire da \(S_1\) e $S_2 nel seguente modo
\[\begin{split} s_i^2 = \sum\limits_{\mathbf{x} \in C_i} (\mathbf{w}^T \mathbf{x} - m_i)^2 &= \sum\limits_{\mathbf{x} \in C_i} (\mathbf{w}^T \mathbf{x} - \mathbf{w}^T \mathbf{m}_i)^2 \\ &= \sum\limits_{\mathbf{x} \in C_i} (\mathbf{w}^T \mathbf{x} - \mathbf{w}^T \mathbf{m}_i) (\mathbf{w}^T \mathbf{x} - \mathbf{w}^T \mathbf{m}_i) \\ &= \sum\limits_{\mathbf{x} \in C_i} (\mathbf{w}^T \mathbf{x} - \mathbf{w}^T \mathbf{m}_i) ( \mathbf{x}^T \mathbf{w} - \mathbf{m}_i^T \mathbf{w}) \\ &= \sum\limits_{\mathbf{x} \in C_i} \Big( \mathbf{w}^T (\mathbf{x} - \mathbf{m}_i) \Big) \Big( (\mathbf{x} - \mathbf{m}_i)^T \mathbf{w} \Big) \\ &= \sum\limits_{\mathbf{x} \in C_i} \mathbf{w}^T (\mathbf{x} - \mathbf{m}_i) (\mathbf{x} - \mathbf{m}_i)^T \mathbf{w} \\ &= \mathbf{w}^T \Bigg( \sum\limits_{\mathbf{x} \in C_i} (\mathbf{x} - \mathbf{m}_i) (\mathbf{x} - \mathbf{m}_i)^T \Bigg) \mathbf{w} \\ &= \mathbf{w}^T \mathbf{S}_i \mathbf{w} \\ \end{split}\]
Questo comporta che, definendo le seguenti due quantità:
total within-class covariance matrix
\[\mathbf{S}_W = \mathbf{S}_1 + \mathbf{S}_2\]
between-class covariance matrix
\[\mathbf{S}_B = (\mathbf{m}_2 - \mathbf{m}_1)(\mathbf{m}_2 - \mathbf{m}_1)^T\]
Possiamo riscrivere il fisher criterion nel seguente modo
\[\begin{split} J(\mathbf{w}) &= \frac{(m_2 - m_1)^2}{s_1^2 + s_2^2} \\ &= \frac{(\mathbf{w}^T \mathbf{m}_2 - \mathbf{w}^T \mathbf{m}_1)^2}{\mathbf{w}^T \mathbf{S}_1 \mathbf{w} + \mathbf{w}^T \mathbf{S}_2 \mathbf{w}} \\ &= \frac{(\mathbf{w}^T \mathbf{m}_2 - \mathbf{w}^T \mathbf{m}_1) (\mathbf{w}^T \mathbf{m}_2 - \mathbf{w}^T \mathbf{m}_1)}{\mathbf{w}^T \mathbf{S}_1 \mathbf{w} + \mathbf{w}^T \mathbf{S}_2 \mathbf{w}} \\ &= \frac{\mathbf{w}^T (\mathbf{m}_2 - \mathbf{m}_1) (\mathbf{m}_2 - \mathbf{m}_1)^T \mathbf{w}}{\mathbf{w}^T \mathbf{S}_1 \mathbf{w} + \mathbf{w}^T \mathbf{S}_2 \mathbf{w}} \\ &= \frac{\mathbf{w}^T \mathbf{S}_B \mathbf{w}}{\mathbf{w}^T \mathbf{S}_W \mathbf{w}} \\ \end{split}\]
Come abbiamo fatto nel caso precedente, l'idea è sempre quella di massimizzare \(J(\mathbf{w})\) rispetto a \(\mathbf{w}\) calcolando il gradiente e settandolo a \(\mathbf{0}\).
In questo caso il gradiente è dato dalla seguente espressione
\[\frac{\partial}{\partial \mathbf{w}} \frac{\mathbf{w}^T \mathbf{S}_B \mathbf{w}}{\mathbf{w}^T \mathbf{S}_W \mathbf{w}} = 2\frac{(\mathbf{w}^T \mathbf{S}_B \mathbf{w}) \mathbf{S}_W \mathbf{w} - (\mathbf{w}^T \mathbf{S}_W \mathbf{w})\mathbf{S}_B \mathbf{w}}{(\mathbf{w}^T \mathbf{S}_W \mathbf{w})(\mathbf{w}^T \mathbf{S}_W \mathbf{w})^T}\]
Che una volta impostato a \(\mathbf{0}\) ci permette di ottenere
\[(\mathbf{w}^T \mathbf{S}_B \mathbf{w}) \mathbf{S}_W \mathbf{w} = (\mathbf{w}^T \mathbf{S}_W \mathbf{w}) \mathbf{S}_B \mathbf{w}\]
Osservando che:
\(\mathbf{w}^T \mathbf{S}_B \mathbf{w}\) è uno scalare \(c_B\)
\(\mathbf{w}^T \mathbf{S}_W \mathbf{w}\) è uno scalare \(c_W\)
\((\mathbf{m}_2 - \mathbf{m}_1)^T \mathbf{w}\) è uno scalare \(C_m\)
otteniamo che possiamo scrivere la condizione di prima nel seguente modo
\[c_B \mathbf{S}_W \mathbf{w} = c_W \mathbf{S}_B \mathbf{w}\]
Ricordandoci poi la definizione di \(\mathbf{S}_B\) otteniamo
\[c_W \mathbf{S}_B \mathbf{w} = c_W (\mathbf{m}_2 - \mathbf{m}_1) (\mathbf{m}_2 - \mathbf{m}_1)^T \mathbf{w} = c_W (\mathbf{m}_2 - \mathbf{m}_1) c_m\]
e quindi
\[\mathbf{w} = \frac{c_W c_m}{c_B} \mathbf{S}_W^{-1} (\mathbf{m}_2 - \mathbf{m}_1)\]
Dato che noi siamo interessati solamente alla direzione di \(\mathbf{w}\), possiamo considerare la seguente soluzione
\[\hat{\mathbf{w}} = \mathbf{S}_W^{-1} (\mathbf{m}_2 - \mathbf{m}_1) = (\mathbf{S}_1 + \mathbf{S}_2)^{-1} (\mathbf{m}_2 - \mathbf{m}_1)\]
Andiamo adesso a vedere come stimare il valore di treshold che ci permette di classificare i vari elementi nelle due classi a partire dalla direzione calcolata \(\mathbf{w}\).
L'idea è quella di modellare la distribuzione delle proiezioni dei punti \(y = \mathbf{w}^T \mathbf{x}\) come una distribuzione gaussiana e stimare la media e la varianza di tale distribuzione utilizzando le seguenti formule
\[\begin{split} m_i &= \frac{1}{n_i} \sum\limits_{\mathbf{x} \in C_i} \mathbf{w}^T \mathbf{x} \;\;\; \text{(media)} \\ \\ \sigma_i^2 &= \frac{1}{n_i - 1} \sum\limits_{\mathbf{x} \in C_i} (\mathbf{w}^T \mathbf{x} - m_i)^2 \;\;\; \text{(varianza)} \end{split}\]
dove \(n_i\) è il numero degli elementi nel training set facenti parte della classe \(C_i\).
Tramite la regola di Bayes si derivano poi le probabilità delle classi
\[\begin{split} P(C_i | y) &\propto P(y|C_i) P(C_i) \\ &= P(y|C_i) \cdot \frac{n_i}{n_1 + n_2} \\ &\propto n_i e ^{-\frac{(y - m_i)^2}{2 \sigma_i^2}} \\ \end{split}\]
Il valore di threshold \(\tilde{y}\) è quindi definito come il minimo \(y\) tale che
\[\frac{P(C_2 | y)}{P(C_1 | y)} = \frac{n_2}{n_1} \frac{P(y|C_2)}{P(y|C_1)} > 1\]
Il terzo metodo di classificazione lineare che consideriamo è quello del percettrone (percepron). Questo metodo è stato introdotto negli anni '60s e anche se presenta una serie di limiti, mantiene comunque una importante significanza storica in quanto è stato il primo esempio di approccio di tipo neurale o connessionistico, che successivamente ha dato origine alle reti neurali.
Il percettrone è un modello semplice di un singolo neurone, nel senso che a partire da certi valori di input fornisce un singolo output simulando a grandi linee il funzionamento di un neurone all'interno del nostro cervello.
I neuroni nel nostro cervello infatti sono collegati tra loro attraverso delle complesse reti. Essi funzionano secondo un modello alquanto semplice: hanno un valore soglia (threhsold), e quando le scariche ricevute dai neuroni a cui sono collegati sommate superano questa threshold, il neurone a sua volta scarica verso altri neuroni.
Considerato da solo, il percettrone ci permette di effettuare risolvere la classificazione binaria. Detto questo, ci sono alcuni limiti significativi da tenere a mente, tra cui.
Non è possibile valutarlo in termine di probabilità.
Il modello funziona solamente quando le classi sono linearmente separabili.
Mentre la prima condizione non è poi così grave, in quanto vale anche per altri modelli già visti, la seconda condizione invece è molto più forte, in molti casi non è verificata, e in particolare non è possibile da valutare a priori se la condizione è verificata o no.
Questo significa che nel caso in cui le classi sono linearmente separabili, allora l'algoritmo del percettrone converge ad un separatore lineare. Se invece le classi non sono linearmente separabili, allora l'algoritmo non converge ma continua a ciclare in un insieme di possibili soluzioni.
Il percettrone corrisponde ad un modello di classificazione binaria così descritto:
All'elemento \(\mathbf{x}\) da classificare è possibile applicare una funzione base non lineare per ottenere \(\phi(\mathbf{x})\). Questo passo non è strettamente necessario, e il modello funziona anche quando la funzione base è l'identità.
La classificazione viene effettuata in base al segno della combinazione lineare delle features \(\mathbf{w}^T \phi(\mathbf{x})\). Ovvero,
\[y(\mathbf{x}) = f(\mathbf{w}^T \phi(\mathbf{x}))\]
dove,
\[f(i) = \begin{cases} -1 & i < 0 \\ 1 & i \geq 0 \\ \end{cases}\]
Quando \(y(\mathbf{x}) = 1\) diciamo che \(\mathbf{x} \in C_1\), mentre quando \(y(\mathbf{x}) = -1\) diciamo che \(\mathbf{x} \in C_2\). Ad ogni elemento \(\mathbf{x}_i\) del training set associamo quindi un target value \(t_i \in \{-1, 1\}\) a seconda se \(\mathbf{x}_i \in C_2\) oppure \(\mathbf{x}_i \in C_1\).
Observation: Come è possibile vedere, il percettrone è un particolare modello lineare generalizzato in cui la funzione \(f(\cdot)\) è la funzione segno.
Come avviene molto spesso, l'apprendimento di un modello parte dalla definizione di una funzione di costo. Il modello infatti tipicamente è ottenuto minimizzando tale funzione di costo.
In questo caso una funzione di costo naturale che in generale potrebbe aver senso utilizzare è la funzione che calcola il numero di elementi classificati male nel training set.
Questo tipo di funzione però sarebbe piecewise constant, e quindi non potremmo utilizzare la tecnica dell'ottimizzazione del gradiente. L'idea sarebbe quindi quella di utilizzare una funzione di costo che sia piecewise linear.
Procediamo quindi cercando di definire una funzione del genere.
Ricordiamo che noi vogliamo trovare un vettore di parametri \(\mathbf{w}\) tale che, per ogni \(\mathbf{x}_i\)
\(\mathbf{w}^T \phi(\mathbf{x}_i) > 0\) se \(\mathbf{x}_i \in C_1\)
\(\mathbf{w}^T \phi(\mathbf{x}_i) < 0\) se \(\mathbf{x}_i \in C_2\)
Queste due condizioni possono essere riassunte utilizzando il valore target \(t_i\) nel seguente modo
\[\mathbf{w}^T \phi(\mathbf{x}_i) t_i > 0\]
Ogni eleento \(\mathbf{x}_i\) fornisce un contributo alla funzione di costo utilizzando il seguente schema:
Il contributo è \(0\) se l'elemento è classificato in modo corretto.
Il contributo è \(-\mathbf{w}^T \phi(\mathbf{x}_i) t_i > 0\), se \(\mathbf{x}_i\) è classificato male.
Sia quindi \(\mathcal{M}\) l'insieme degli elementi classificati male. La funzione di costo è data dalla seguente espressione
\[E_p(\mathbf{w}) = - \sum\limits_{\mathbf{x}_i \in \mathcal{M}} \mathbf{w}^T \phi(\mathbf{x}_i) t_i\]
A questo punto possiamo applicare l'ottimizzazione del gradiente alla funzione \(E_p(\mathbf{w})\) per ottenere
\[\mathbf{w}^{(k+1)} = \mathbf{w}^{(k)} - \eta \frac{\partial E_p(\mathbf{w})}{\partial \mathbf{w}} \Big|_{\mathbf{w}^{(k)}}\]
Notando poi che il gradiente della funzione costo rispetto a \(\mathbf{w}\) è dato dalla seguente espressione
\[\frac{\partial E_p(\mathbf{w})}{\partial \mathbf{w}} = - \sum\limits_{\mathbf{x}_i \in \mathcal{M}} \phi(\mathbf{x}_i) t_i\]
possiamo esprimere la discesa del gradiente come segue
\[\mathbf{w}^{(k+1)} = \mathbf{w}^{(k)} + \eta \sum\limits_{\mathbf{x}_i \in \mathcal{M_k}} \phi(\mathbf{x}_i) t_i\]
dove \(\mathcal{M}_k\) è l'insieme dei punti classificati male dal modello definito dai parametri \(\mathbf{w}^{(k)}\).
Nel caso del percettrone in realtà si applica una variante della discesa del gradiente, detta stochastic gradient descent. In questa versione ad ogni step consideriamo solamente il gradiente rispetto ad un singolo elemento
\[\mathbf{w}^{(k+1)} = \mathbf{w}^{(k)} + \eta \phi(\mathbf{x}_i) t_i\]
dove \(\mathbf{x}_i \in \mathcal{M}_k\) e il valore di \(\eta > 0\) (scale factor) controllano l'impatto di un elemento mal classificato sulla funzione di costo.
Il metodo si basa sull'applicare la formula di prima iterando ciclicamente su ogni elemento del training set. Ogni volta che incontriamo un elemento ben classificato non facciamo nulla, e ogni volta che incontriamo un elemento mal classificato aggiorniamo i parametri con la formula. Tale metodo è riportato a seguire

Questo procedimento
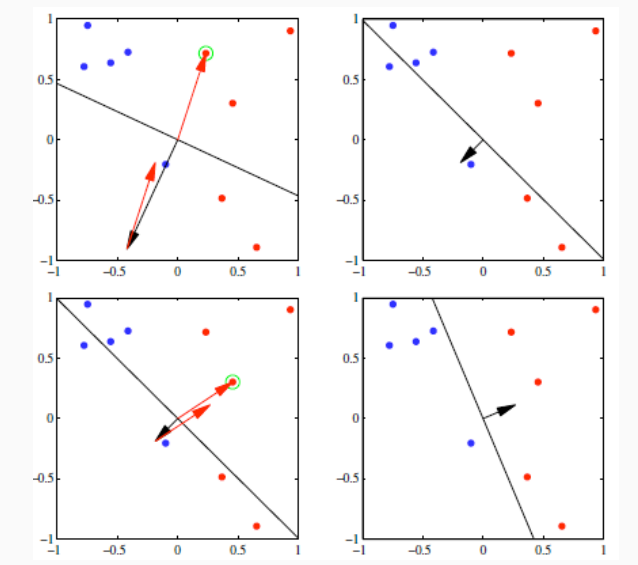
È possibile dimostrare che se se \(\mathbf{x}_i\) è ben classificato, allora \(\mathbf{w}^{(k)}\) non cambia, mentre se \(\mathbf{x}_i\) è mal classificato allora il suo contributo al costo finale cambia come segue
\[\begin{split} -(\mathbf{w}^{(k+1)})^T \phi(\mathbf{x}_i) t_i &= -(\mathbf{w}^{(k)})^T \phi(\mathbf{x}_i) t_i - \eta (\phi(\mathbf{x}_i) t_i)^T \phi(\mathbf{x}_i) t_i \\ &= -(\mathbf{w}^{(k)})^T \phi(\mathbf{x}_i) t_i - \eta ||\phi(\mathbf{x}_i)||^2 \\ &< -(\mathbf{w}^{(k)})^T \phi(\mathbf{x}_i) t_i \\ \end{split}\]
Come è possibile vedere, il contributo rispetto al singolo elemento \(\mathbf{x}_i\) tende a diminuire. In ogni caso, è importante notare che questa diminuzione è relativa solo al singolo elemento, e non è globale. Potrebbe infatti succedere che passando da \(\mathbf{w}^{(k)}\) a \(\mathbf{w}^{(k+1)}\) il costo totale aumenti in quanto qualche altro elemento viene classificato male.
È possibile dimostrare che nel caso in cui le classi siano linearmente separabili allora l'algoritmo visto prima converge alla soluzioen corretta in un numero finito di apssi.
Se invece il training set non è linearmente separabile, allora non ho nessuna garanzia di convergenza in tempo finito.
Possiamo visualizzare la struttura di un percettrone con il seguente schema