ML - 11 - Probabilistic Classification I
Lecture Info
Date:
Lecturer: Giorgio Gambosi
Slides: (ml_06_probclass-slides.pdf)
In questa lezione abbiamo iniziato la trattazione della probabilistic classification. Inizialmente abbiamo ripassato i concetti fondamental dietro ai naive bayes classifiers. Abbiamo poi continuato generalizzando quanto visto per parlare dei generative models. Infine, abbiamo introdotto un nuovo classificatore probabilistico che fa utilizzo di modelli generativi tramite la gaussian discriminant analysis (GDA).
1 Naive Bayes Classifiers
Per iniziare il discorso sui classificatori probabilistici ripassiamo velocemente i classificatori Naive Bayes.
1.1 Language Models
I classificatori Naive Bayes utilizzano dei modello di linguaggio, che sono delle distribuzione di probabilità sui termini di un vocabolario (termini che tipicamente compaiono in una grande collezione di documenti).
Un modello di linguaggio è quindi un modello generativo che può essere utilizzato per generare il prossimo termine che apparirà in un dato testo.
Nel contesto di utilizzo dei classificatori Naive Bayes si assume l'ipotesi bag of words, che vede un documento come un multiset di termini. Utilizzando questa ipotesi quindi si perde l'informazione sulla particolare sequenza in cui i termini compaiono nei documenti.
1.2 Bayesian Classifiers
A partire da un modello di linguaggio è possibile derivare dei classificatori di documenti in due o più classi tramite l'applicazione della regola di Bayes.
In particolare, date due classi \(C_1, C_2\), se si assume che per ogni documento \(d\) le probabilità di appartenenza alle due classi \(P(C_1|d)\), \(P(C_2|d)\) sono note, allora è possibile applicare qualche criterio di confronto tra questi valori di probabilità per assegnare il documento \(d\) ad una data classe. Ad esempio si potrebbe assegnare \(d\) alla classe con la probabilità più alta.
Come facciamo però a derivare queste probabilità \(P(C_k|d)\)? L'idea è quella di applicare la regola di Bayes. Infatti, sia \(\mathcal{C}_i\) una collezione di documenti facenti parte della classe \(C_i\). Applicando Bayes otteniamo
\[P(C_k|d) = \frac{P(d|C_k) P(C_k)}{P(d)} \propto P(d|C_k) P(C_k)\]
Notiamo che ignoriamo l'evidenza \(P(d)\) in quanto è la stessa per ogni classe, e dunque può essere ignorata. Anche ignorando \(P(d)\) in ogni caso, per poter calcolare \(P(C_k|d)\) dobbiamo comunque calcolare sia \(P(d|C_k)\) che \(P(C_k)\).
1.2.1 Computing \(P(C_k)\)
Per stimare \(P(C_k)\) possiamo applicare lo stimatore ML (Maximum Likelihood) a partire dalle collezioni \(\mathcal{C}_1 \mathcal{C}_2\) per ottenere
\[\begin{split} P(C_1) &= \frac{|\mathcal{C}_1|}{|\mathcal{C}_1| + |\mathcal{C}_2|} \\ \\ P(C_2) &= \frac{|\mathcal{C}_2|}{|\mathcal{C}_1| + |\mathcal{C}_2|} \\ \end{split}\]
1.2.2 Computing \(P(d|C_k)\)
Per sitmare le probabilità \(P(d|C_k)\) invece utilizziamo l'ipotesi bag of words per considerare il documento \(d\) come un multiset di \(n_d\) termini
\[d = \{\overline{t}_1, \overline{t}_2, \ldots, \overline{t}_{n_d}\}\]
Tramite la regola del prodotto delle probabilità otteniamo
\[\begin{split} P(d|C_k) &= P(\overline{t}_1, \overline{t}_2, \ldots, \overline{t}_{n_d} | C_k) \\ &= P(\overline{t}_1 | C_k) P(\overline{t}_2 | \overline{t}_1, C_k) \cdots P(\overline{t}_{n_d} | \overline{t}_1, \overline{t}_2, \ldots, \overline{t}_{n_{d - 1}}C_k) \\ \end{split}\]
Per semplificare ulteriormente il calcolo introduciamo quindi un'ulteriore ipotesi semplificativa, nota con il nome di naïve naive bayes assumption. Questa ipotesi ci dice che i termini sono pairwise conditionally independent, ovvero che data la classe \(C_k\) si ha che
\[P(\overline{t}_i, \overline{t}_j | C_k) = P(\overline{t}_i | C_k) P(\overline{t}_2 | C_k)\]
Applicando questa uguaglianza al risultato di prima otteniamo
\[\begin{split} P(d|C_k) &= P(\overline{t}_1 | C_k) P(\overline{t}_2 | \overline{t}_1, C_k) \cdots P(\overline{t}_{n_d} | \overline{t}_1, \overline{t}_2, \ldots, \overline{t}_{n_{d - 1}}C_k) \\ &= P(\overline{t}_1 | C_k) P(\overline{t}_2 | C_k) \cdots P(\overline{t}_{n_d} | C_k) \\ &= \prod\limits_{j = 1}^{n_d} P(\overline{t}_j |C_k) \\ \end{split}\]
2 Generative Models
I modelli della forma \(P(x|C_k)\) sono detti modelli generativi (generative models), proprio per il fatto che possono essere utilizzati per generare nuovi elementi.
Ad esempio, nel caso di Naive Bayes Classifiers visti prima, una volta calcolate le probabilità \(P(x|C_k)\) per ogni classe \(C_k\), è possibile effettuare del sampling da queste distribuzioni per generare documenti random che sono statisticamente equivalenti ai documenti presenti nella collezione utilizzata per derivare il modello.
A partire dalle probabilità \(P(x|C_k)\) e \(P(C_k)\) possiamo poi utilizzare la regola di Bayes per derivare la probabilità a posteriori \(P(C_k|x)\). Queste probabilità possono essere utilizzate per effettuare una classificazione probabilistica.
2.1 Binary Case (Sigmoid)
Consideriamo il caso di classificazione binaria, e vediamo cosa succede quando deriviamo le probabilità a posteriori utilizzando la regola di Bayes.
\[P(C_1 | x) = \frac{P(x|C_1) P(C_1)}{P(x|C_1)P(C_1) + P(x|C_2) P(C_2)} = \frac{1}{1 + \frac{P(x|C_2) P(C_2)}{P(x|C_1)P(C_1)}}\]
Definiamo quindi la seguente quantità interessante
\[a := \log{\frac{P(x|C_1) P(C_1)}{P(x|C_2)P(C_2)}} = \log{\frac{P(C_1|x)}{P(C_2|x)}}\]
questa quantità prende il nome di log odds, in quanto è il logaritmo del rapporto tra le posterior probabilities. Osserviamo che
\[\begin{split} P(C_1 | x) &= \frac{1}{ 1+ e^{-a}} =: \sigma(a) \\ \\ P(C_2 | x) &= 1 - \frac{1}{1 + e^{-a}} = \frac{1}{1 + e^a} \\ \end{split}\]
La funzione \(\sigma(x)\) è detta logistic function (functione logistica) o sigmoid (sigmoide), e presenta la seguente forma
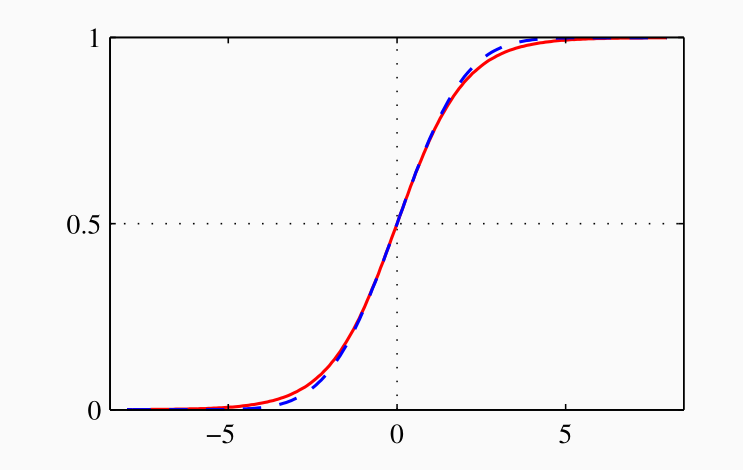
La funzione logistica è un'approssimazione smooth della funzione soglia e presenta le seguenti proprietà
\[\begin{split} \sigma(-x) &= 1 - \sigma(x) \\ \\ \frac{d }{d x} \sigma(x) &= \sigma(x)(1 - \sigma(x)) \\ \end{split}\]
2.2 General Case (Softmax)
Nel caso in cui abbiamo più di due classi \(K > 2\), la formula generale per la probabilità a posteriori è la seguente
\[P(C_k | x) = \frac{P(x|C_k) P(C_k)}{\sum_j P(x|C_j) P(C_j)}\]
Per ogni \(k = 1, \ldots, K\) si definisce quindi
\[a_k(x) = \log{\Big(P(x|C_k) \cdot P(C_k)\Big)} = \log{P(x|C_k)} + \log{P(C_k)}\]
Così facendo possiamo scrivere
\[P(C_k | x) = \frac{e^{a_k}}{\sum_j e^{a_j}} =: s(a_k)\]
La funzione \(s(x)\) è chiamata softmax (o normalized exponential) ed è l'estensione della funzione sigmoid al caso \(K > 2\). Tale funzione può essere anche vista come una versione smoothed del massimo, nel senso che se esiste un \(a_k\) tale che \(a_k >> a_j\) per ogni \(j \neq k\), allora \(s(a_k) \approx 1\) e \(s(a_j) \approx 0\) per ogni \(j \neq k\).
3 Gaussian Discriminant Analysis
Introduciamo adesso un classificatore generatico diverso dal tipico classificatore Naive Bayes. In particolare consideriamo il classificatore basato sulla Gaussian discriminant analysis (GDA).
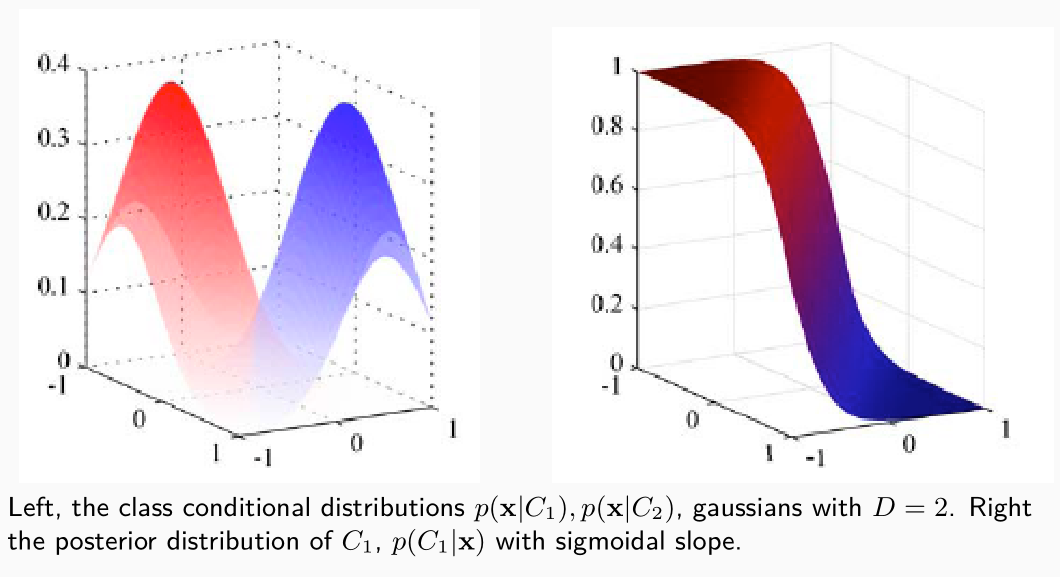
Dato che l'approccio utilizzato è sempre di tipo generativo, si parte assumendo la forma delle distribuzioni condizionate alle classi, ovvero delle distribuzioni \(P(x|C_k)\) per ogni classe \(C_k\) presa in considerazione. L'idea infatti è quella di stimare \(P(x|C_k)\) per poi calcolare facilmente le posterior probability \(P(C_k|x)\) che verranno utilizzate per effettuare la classificazione.
Seguendo l'approccio GDA si assume quindi che tutte le distribuzioni \(P(x|C_k)\) sono gaussiane.
3.1 Same Covariance Matrix
Nel primo caso che andiamo analizzare non solo assumiamo che le distribuzioni \(P(x|C_k)\) siano tutte gaussiane, ma assumiamo anche che hanno tutte la stessa matrice di covarianza \(\mathbf{\Sigma}\) di size \(D \times D\). Così facendo otteniamo
\[P(x|C_k) = \frac{1}{(2\pi)^{d/2} |\mathbf{\Sigma}|^{1/2}} \cdot \text{exp}\Big(-\frac12 (x - \mathbf{\mu}_k)^T \mathbf{\Sigma}^{-1} (x - \mathbf{\mu}_k) \Big)\]
3.1.1 Binary Case
Se abbiamo due classi \((K = 2)\) avevamo visto che
\[P(C_1 | x) = \sigma(a(x))\]
dove
\[a(x) = \log{\frac{P(x|C_1) P(C_1)}{P(x|C_2) P(C_2)}}\]
Andando a sostituire l'espressione di prima per \(P(x|C_k)\) otteniamo quindi
\[\begin{split} a(x) &= \log{\frac{P(x|C_1) P(C_1)}{P(x|C_2) P(C_2)}} \\ &= \log{\frac{\frac{1}{(2\pi)^{d/2} |\mathbf{\Sigma}|^{1/2}} \cdot \text{exp}\Big(-\frac12 (x - \mathbf{\mu}_1)^T \mathbf{\Sigma}^{-1} (x - \mathbf{\mu}_1) \Big)P(C_1)}{\frac{1}{(2\pi)^{d/2} |\mathbf{\Sigma}|^{1/2}} \cdot \text{exp}\Big(-\frac12 (x - \mathbf{\mu}_2)^T \mathbf{\Sigma}^{-1} (x - \mathbf{\mu}_2) \Big)P(C_2)}} \\ &= \frac12 \Big(\mathbf{\mu}_2^T \mathbf{\Sigma}^{-1} \mathbf{\mu}_2 - x^T \mathbf{\Sigma}^{-1} \mathbf{\mu}_2 - \mathbf{\mu}_2^T \mathbf{\Sigma}^{-1} x\Big) \\ &\;\;\;\;\; - \frac12 \Big( \mathbf{\mu}_1^T \mathbf{\Sigma}^{-1}\mathbf{\mu}_1 - x^T \mathbf{\Sigma}^{-1} \mathbf{\mu}_1 - \mathbf{\mu}_1^T \mathbf{\Sigma}^{-1} x\Big) + \log{\frac{P(C_1)}{P(C_2}}\\ \end{split}\]
Notando poi che i risultati di tutti i prodotti che coinvolgono \(\mathbf{\Sigma}^{-1}\) sono scalari, e in particolare dato che ogni scalare è uguale al suo trasporto, otteniamo che
\[\begin{split} x^T \mathbf{\Sigma}^{-1} \mathbf{\sigma}_1 &= \sigma_1^T \mathbf{\Sigma}^{-1} x \\ \\ x^T \mathbf{\Sigma}^{-1} \mathbf{\sigma}_2 &= \sigma_2^T \mathbf{\Sigma}^{-1} x \\ \end{split}\]
possiamo quindi semplificare per ottenere
\[\begin{split} a(x) &= \frac12 \Big(\mu_2^T \mathbf{\Sigma}^{-1} \mu_2 - \mu_1^T \mathbf{\Sigma}^{-1} \mu_1 \Big) + \Big(\mu_1^T \mathbf{\Sigma}^{-1} - \mu_2^T \mathbf{\Sigma}^{-2} \Big)x + \log{\frac{P(C_1)}{P(C_2)}} \\ &= \mathbf{w}^T \mathbf{x} + w_0 \\ \end{split}\]
con
\[\begin{split} \mathbf{w} &= \mathbf{\Sigma}^{-1}(\mu_1 - \mu_2) \\ \\ w_0 &= \frac12 \Big(\mu_2^T \mathbf{\Sigma}^{-1} \mu_2 - \mu_1^T \mathbf{\Sigma}^{-1} \mu_1 \Big) + \log{\frac{P(C_1)}{P(C_2)}} \\ \end{split}\]
Alla fine abbiamo quindi ottenuto
\[P(C_1 | x) = \sigma(\mathbf{w}^T x + w_0)\]
Dove \(\mathbf{w}\) e \(w_0\) possono essere stimati a partire dal training set. Una volta calcolate queste probabilità possiamo poi classificare l'elemento \(x\) in una delle due classi \(C_1\) o \(C_2\).
3.1.2 Discriminant Function
Volendo vedere la funzione discriminante che partiziona il piano tra i punti appartenenti alla classe \(C_1\) e quelli appartenenti alla classe \(C_2\) l'idea è quelal di imporre la condizione
\[P(C_1|x) = P(C_2|x) \iff \sigma(a(x)) = \sigma(-a(x))\]
e dato che la funzione è monotona questo equivale a dire che \(a(x) = -a(x)\) e quindi \(a(x) = 0\). Il luogo dei punti che fa da confine tra le due classi è quindi descritto dai punti che soddisfano la seguente equazione
\[\mathbf{w}^T x + w_0 = 0\]
sostituendo in termini dei parametri delle gaussiane sottostanti otteniamo
\[\mathbf{\Sigma}^{-1}(\mu_1 - \mu_2)x + \frac12(\mu_2^T \mathbf{\Sigma}^{-1} \mu_2 - \mu_1^T \mathbf{\Sigma}^{-1} \mu_1) + \log{\frac{P(C_2)}{P(C_1)}} = 0\]
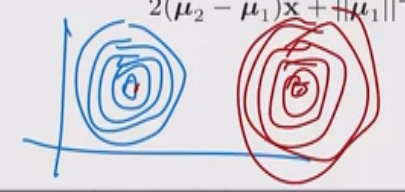
Se poi assumiamo che la matrice di covarianza è diagonale a valori costanti, ovvero che non ci sia correlazione tra features diverse, in formula \(\mathbf{\Sigma} = \lambda \mathbf{I}\), allora la funzione discriminante è data da
\[2(\mu_2 - \mu_1) x + ||\mu_1||^2 - ||\mu_2||^2 + 2 \lambda \log{\frac{P(C_2)}{P(C_1)}} = 0\]
Geometricamente questa ulteriore assunzione ci dice che le due distribuzioni hanno simmetrica sferica.
3.1.3 Multiple Classes
Quanto visto per il caso binario può essere facilmente esteso quando abbiamo più di due classi \((K > 2)\). In questo caso al posto di utilizzare la funzione sigmoid utilizziamo la funzione softmax
\[P(C_k|x) = s(a_k(x))\]
con
\[a_k = \log{\Big(P(x|C_k)P(C_k)\Big)}\]
Applicando le stesse considerazioni fatte prima si ottiene
\[\begin{split} a_k(x) &= \frac12 \Big(\mu_k^T \mathbf{\Sigma}^{-1} x - \mu_k^T \mathbf{\Sigma}^{-1} \mu_k \Big) + \log{P(C_k)} - \frac{d}{2} \log{(2\pi)} - \frac12 \log{|\mathbf{\Sigma}|} \\ &= \mathbf{w}_k^T x + w_{0,k} \\ \end{split}\]
e quindi anche \(a_k(x)\) è ottenuta tramite una combinazione lineare delle features.
3.1.4 Decision Boundaries
Nel caso in cui abbiamo più classi i decision boundaries corrispondono alle regioni in cui ci sono due classi \(C_j\) e \(C_k\) tali per cui le probabilità a posteriori sono uguali tra loro e sono più grandi di tutte le altre classi. In formula,
\[P(C_k|x) = P(C_j|x) \;\;\;\;\;,\;\;\;\; P(C_i|x) < P(C_k|x) \,\,\,\,\,\, i \neq j, k\]
In questo caso quindi si ha
\[e^{a_k(x)} = e^{a_j(x)} \;\;\;\;\;,\;\;\;\; e^{a_i(x)} < e^{a_k(x)} \,\,\,\,\,\, i \neq j, k\]
e quindi
\[a_k(x) = a_j(x) \;\;\;\;\;,\;\;\;\; a_i(x) < a_k(x) \,\,\,\,\,\, i \neq j, k\]
ovvero questi boundaries sono lineari.
3.2 Different Covariance Matrices
Nel caso più generale (limitandoci però all'analisi del caso binario con due classi) non imponiamo che le due matrici di covarianza siano la stessa, ma lasciamo la possibilità che le matrici di covarianza di \(P(x|C_1)\) e \(P(x|C_2)\) possono essere diverse.
In questo caso otteniamo
\[\begin{split} a(x) &= \log{\frac{P(x|C_1) P(C_1)}{P(x|C_2) P(C_2)}} \\ &= \log{\frac{\text{exp}(-\frac12 (x - \mu_1)^T \mathbf{\Sigma}_1^{-1}(x - \mu_1))}{\text{exp}(-\frac12 (x - \mu_2)^T \mathbf{\Sigma}_2^{-1}(x - \mu_2))}} + \frac12 \log{\frac{|\mathbf{\Sigma}_2|}{|\mathbf{\Sigma}_1|}} + \log{\frac{P(C_1)}{P(C_2)}} \\ &= \frac12 \Big( (x - \mu_2)^T \mathbf{\Sigma}_2^{-1} (x - \mu_2) - (x - \mu_1)^T \mathbf{\Sigma}_1^{-1}(x - \mu_1)\Big) + \frac12 \log{\frac{|\mathbf{\Sigma}_2|}{|\mathbf{\Sigma}_1|}} + \log{\frac{P(C_1)}{P(C_2)}} \end{split}\]
Ripercorrendo gli stessi passaggi di prima adeguandoci alla nuova situazione, i decision boundaries presentano la seguente forma
\[\Big( (x - \mu_2)^T \mathbf{\Sigma}_2^{-1} (x - \mu_2) - (x - \mu_1)^T \mathbf{\Sigma}_1^{-1}(x - \mu_1)\Big) + \log{\frac{|\mathbf{\Sigma}_2|}{|\mathbf{\Sigma}_1|}} + \log{\frac{P(C_1)}{P(C_2)}} = 0\]
Notiamo che l'espressione presenta dei termini quadratici. Questo significa che le classi possono essere separate (al più) da superfici quadratiche. Dunque il modello ottenuto non è sempre lineare ma può essere quadratico, come mostra il seguente esempio
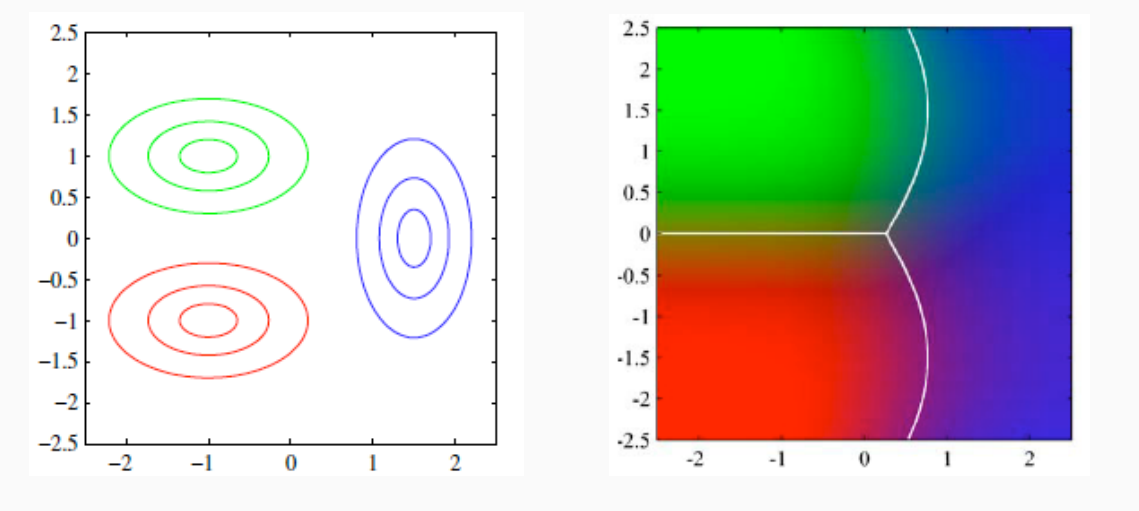
3.3 Estimation with ML
Per applicare quanto abbiamo visto necessitiamo di poter stimare le distribuzioni condizionate \(P(x|C_k)\) a partire dal training set. Per questo questo possiamo utilizzare delle stime ML (Maximum Likelihood).
Per semplicità assumiamo caso binario \(K=2\) e che entrambi le classi condividono la stessa matrice di covarianza \(\mathbf{\Sigma}\). L'idea è quindi quella di stimare \(\mu_1, \mu_2, \mathbf{\Sigma}\) e \(\pi = P(C_1)\), notando che \(P(C_2) = 1 -\pi\).
Consideriamo quindi di avere un training set \(\mathcal{T}\) che include \(n\) coppie di elementi \((x_i, t_i)\) con
\[t_i = \begin{cases} 0 & x_i \in C_2 \\ 1 & x_i \in C_1 \\ \end{cases}\]
Se \(x \in C_1\) allora
\[P(x, C_1) = P(x|C_1) P(C_1) = \pi \cdot \mathcal{N}(x|\mathbf{\mu}_1, \mathbf{\Sigma})\]
se invece \(x \in C_2\) allora
\[P(x, C_2) = P(x|C_2) P(C_2) = (1 - \pi) \cdot \mathcal{N}(x | \mathbf{\mu}_2, \mathbf{\Sigma})\]
L'espressione del likelihood del training set \(\mathcal{T}\) è quindi data da
\[L(\pi, \mu_1, \mu_2, \mathbf{\Sigma}| \mathcal{T}) =\prod\limits_{i = 1}^n \Big(\pi \cdot \mathcal{N}(x|\mathbf{\mu}_1, \mathbf{\Sigma})\Big)^{t_i} \cdot \Big((1 - \pi) \cdot \mathcal{N}(x|\mathbf{\mu}_2, \mathbf{\Sigma})\Big)^{1 - t_i}\]
la corrispondente log-likelihood è quindi data da
\[\begin{split} l(\pi, \mu_1, \mu_2, \mathbf{\Sigma} | \mathcal{T}) &= \sum\limits_{i = 1}^n \Big(t_i \log{\pi} + t_i \log{(\mathcal{N}(x_i | \mu_1, \mathbf{\Sigma}))} \Big) + \\ & \;\;\; + \sum\limits_{i = 1}^n \Big( (1 - t_i) \log{(1 - \pi)} + (1 - t_i)\log{(\mathcal{N}(x_i|\mu_2, \mathbf{\Sigma}))} \Big)\\ \end{split}\]
A questo punto procediamo annullando la derivata rispetto ai vari parametri.
3.3.1 Estimating \(\pi\)
La derivata della log-likelihood rispetto a \(\pi\) è data da
\[\begin{split} \frac{\partial l}{\partial \pi} &= \frac{\partial }{\partial \pi} \sum\limits_{i = 1}^n \Big( t_i \log{\pi} + (1 - t_i) \log{(1 - \pi)}\Big) \\ &= \sum\limits_{i = 1}^n \Big(\frac{t_1}{\pi} - \frac{(1 - t_i)}{1 - \pi}\Big) \\ &= \frac{n_1}{\pi} - \frac{n_2}{1 - \pi} \\ \end{split}\]
che quando impostata a \(0\) ci da come risultato
\[\pi = \frac{n_1}{n}\]
3.3.2 Estimating \(\mu_1, \mu_2\)
Allo stesso modo, il massimo rispetto alle medie \(\mu_1\) (e \(\mu_2)\) può essere calcolato tramite il gradiente della log-likelihood
\[\begin{split} \frac{\partial l}{\partial \mu_1} &= \frac{\partial}{\partial \mu_1} \sum\limits_{i = 1}^n t_i \log{(\mathcal{N}(x_i | \mu_1, \mathbf{\Sigma}))} \\ &= \ldots \\ &= \mathbf{\Sigma}^{-1} \sum\limits_{i = 1}^n t_i(x_i - \mu_1) \\ \end{split}\]
notiamo quindi che abbiamo \(\frac{\partial l}{\partial \mu_1} = 0\) quando
\[\sum\limits_{i = 1}^n t_i x_i = \sum\limits_{i = 1}^n t_i \mu_1 \]
e quindi
\[\mu_1 = \frac{1}{n_1} \sum\limits_{x_i \in C_1} x_i\]
che è proprio il punto medio degli elementi facente parte della classe \(C_1\).
3.3.3 Estimating \(\mathbf{\Sigma}\)
Infine, per quanto riguarda \(\mathbf{\Sigma}\), è possibile vedere che
\[\mathbf{\Sigma} = \frac{n_1}{n} \mathbf{S}_1 + \frac{n_2}{n} \mathbf{S}_2\]
dove
\[\begin{split} \mathbf{S}_1 &= \frac{1}{n_1} \sum\limits_{x_1 \in C_1} (x_i - \mu_1) (x_i - \mu_1)^T \\ \\ \mathbf{S}_2 &= \frac{1}{n_2} \sum\limits_{x_1 \in C_2} (x_i - \mu_2) (x_i - \mu_2)^T \\ \end{split}\]