ML - 13 - Probabilistic Classification III
Lecture Info
Date:
Lecturer: Giorgio Gambosi
Slides: (ml_06_probclass-slides.pdf)
In questa lezione abbiamo introdotto l'approccio discriminativo per effettuare la classificazione probabilistica, discutendo in particolare il modello della logistic regression. Abbiamo poi parlato del metodo di Netwon-Raphson per calcolare i punti di massimo/minimo di una funzione in modo iterativo. Per finire, abbiamo discusso dell'iterated reweighted least squares come modo ulteriore di calcolare il punto di minimo della loss function nel caso della regressione logistica.
1 Discriminative Approach
Nella trattazione dei modelli generativi per la classificazione probabilistica abbiamo visto che in molti casi le probabilità che utilizziamo per effettuare la classificazione, ovvero le probabilità delle classi condizionate agli elementi \(P(C_k|x)\), risultano essere descritte in molti casi da un modello lineare generalizzato (GLM).
Un altro approccio per effettuare la classificazione probabilistica, che prende il nome di approccio discriminativo (discriminative approach), consiste nell'assumere direttamente che la probabilità condizionata \(P(C_k|x)\) è un GLM, per poter derivare direttamente i coefficienti del modello tramite una stima ML.
Rispetto al modello generativo il modello discriminativo presenta le seguenti caratteristiche:
Non conoscendo \(P(x|C_k)\), abbiamo meno conoscenza sui dati e perdiamo l'abilità di generare sinteticamente i nuovi dati che siano statisticamente equivalenti a quelli presenti nel training set.
Tipicamente richiede di stimare meno parametri, e dunque permette di ottenere dei modelli più semplici.
Offre delle migliori predizioni nei casi in cui non abbiamo molte informazioni su \(P(x|C_k)\) e quindi qualsiasi ipotesi potremmo fare su tale distribuzione sarebbe povera.
2 Logistic Regression
Il primo modello che utilizza un approccio discriminativo che vediamo è la logistic regression, che abbiamo già considerando studiando il GLM derivante dall'ipotesi che il valore da predirre \(y\) seguiva una distribuzione Bernoulliana.
In questo modello la probabilità condizionata di appartenenza ad una classe è stimata dalla funzione sigmoide applicata a una combinazione lineare delle features. In formula,
\[P(C_1|\mathbf{x}) = \sigma(\mathbf{w}^T \overline{\mathbf{x}}) = \frac{1}{1 + e^{-\mathbf{w}^T \overline{x}}}\]
Osservazione 1: Anche se tutti i risultati che otteniamo saranno scritti utilizzando direttamente le features, è sempre possibile applicare delle funzioni base \(\phi_i()\) senza così facendo cambiare i risultati.
2.1 Degrees of Freedom
Nel caso in cui abbiamo \(d\) features, la logistic regression richiede \(d+1\) coefficienti \(w_0, \ldots, w_d\) ottenuti dal training set.
Questo numero è molto minore rispetto al numero di coefficienti richiesti nel caso in cui scegliessimo di applicare un approccio generativo, ad esempio con una GDA. In quel caso infatti avremmo
\(2d\) coefficienti per i vettori delle medie \(\mu_1, \mu_2\).
Per ogni matrice di covarianza avremmo \(\sum\limits_{i = 1}^d i = d(d+1)/2\) coefficienti.
Per ogni classe una probabilità a priori \(P(C_k)\)
Che in totale risultano essere \(d(d+1) 2d + 1 = d(d + 3) + 1\) coefficienti.
2.2 ML Estimation
Per stimare i parametri del modello assumiamo che gli elementi target del training set fissati i coefficienti del modello possono essere modellati tramite una distribuzione di Bernoulli. Ovvero che
\[P(t_i | x_i \mathbf{w}) = p_i^{t_i}(1 - p_i)^{1 - t_i}\]
dove
\[p_{i} = P(C_1|x_i)\]
Utilizzando poi il fatto di aver assunto inizialmente che \(P(C_1|x_i) = \sigma(\mathbf{w}^T x_i)\) possiamo esprimere la verosomiglianza di un insieme di training \(\mathbf{t}\) dato \(\mathbf{X}\) nel seguente modo
\[\begin{split} P(\mathbf{t}|\mathbf{X}, \mathbf{w}) &= L(\mathbf{w}|\mathbf{X},\mathbf{t}) \\ &= \prod\limits_{i = 1}^n P(t_i| x_i, \mathbf{w}) \\ &= \prod\limits_{i = 1}^n p_i^{t_i} (1 - p_i)^{1 - t_i} \\ \end{split}\]
e quindi la log-likelihood è data da
\[\begin{split} l(\mathbf{w}|\mathbf{X}, \mathbf{t}) &= \log{L(\mathbf{w}|\mathbf{X}, \mathbf{t})} \\ &= \sum\limits_{i = 1}^n \Big( t_i \log{p_i} + (1 - t_i)\log{(1 - p_i)} \Big) \\ \end{split}\]
Osservazione: Tecnicamente piuttosto che considerare \(P(\mathbf{t}|\mathbf{X}, \mathbf{w})\) dovremmo considerare la probabilità di vedere l'intero training set dato il modello \(\mathbf{w}\), ovvero \(P(\mathbf{t}, \mathbf{X} | \mathbf{w})\). Quello che succede però è che utilizzando la regola del prodotto otteniamo
\[P(\mathbf{t}, \mathbf{X} | \mathbf{w}) = P(\mathbf{t} | \mathbf{X}, \mathbf{w}) \cdot P(\mathbf{X} | \mathbf{w})\]
e inoltre possiamo considerare che i punti del training set \(\mathbf{X}\) non dipendano dai parametri del modello \(\mathbf{w}\). Quindi \(P(\mathbf{X} | \mathbf{w}) = P(\mathbf{X})\). Infine, dato che noi vogliamo massimizzare tale valore al variare di \(\mathbf{w}\), possiamo semplicemente eliminare il fattore costante \(P(\mathbf{X})\) e considerare solamente \(P(\mathbf{t} | \mathbf{X}, \mathbf{w})\).
Procediamo quindi calcolando il gradiente della log-likleihood rispetto a \(\mathbf{w}\) è possibile vedere che
\[\frac{\partial (\mathbf{w} | \mathbf{X}, \mathbf{t})}{\partial \mathbf{w}} = \sum\limits_{i = 1}^n (t_i - p_i) \overline{x}_i = \sum\limits_{i = 1}^n (t_i - \sigma(\mathbf{w}^T \overline{x}_i)) \overline{x}_i\]
Notiamo quindi che il gradiente è una combinazione lineare delle features in cui ogni feature viene scalata rispetto alla differenza \((t_i - p_i)\).
2.3 Gradient Ascent
Dato che porre uguale a \(0\) il gradiente e risolvere analiticamente l'espressione risulta molto difficile, è preferibile applicare un metodo iterativo per il calcolo di un massimo locale.
Potremmo ad esempio utilizzare l'algoritmo gradient ascent, dove at ogni iterazione si utilizza la seguente regola di update
\[\begin{split} \mathbf{w}^{(j+1)} &= \mathbf{w}^{(j)} + \alpha \cdot \frac{\partial l(\mathbf{w} | \mathbf{X}, \mathbf{t})}{\partial \mathbf{w}} \Big|_{\mathbf{w}^{(j)}} \\ &= \mathbf{w}^{(j)} + \alpha \sum\limits_{i = 1}^n\Big(t_i - \sigma\big((\mathbf{w}^{(j)})^T \overline{x}_i \big) \Big) \overline{x}_i \\ &= \mathbf{w}^{(j)} + \alpha \sum\limits_{i = 1}^n \Big( t_i - y(x_i)\Big) \overline{x}_i \\ \end{split}\]
Come avevamo già menzionato nel caso della regressione lineare, l'algoritmo appena visto è detto batch gradiant ascent in quanto ad ogni passo il gradiente viene aggiornato rispetto a tutti elementi del training set. Ci sono però altre varianti, tra cui la più semplice è lo stochastic gradiant ascent, in cui si considera solamente un solo elemento del training set.
In alternativa ad ogni passo si può aggiornare un solo coefficiente del modello
\[\begin{split} w_k^{(j+1)} &= w_k^{(j)} + \alpha \frac{\partial l(\mathbf{w} | \mathbf{X}, \mathbf{t})}{\partial w_k} \Big|_{\mathbf{w}^{(j)}} \\ &= w_k^{(j+1)} + \alpha \sum\limits_{i = 1}^n \Big(t_i - \sigma\big((\mathbf{w}^{(j)})^T \overline{x}_i \big) \Big) x_{i,k} \\ &= w_k^{(j+1)} + \alpha \sum\limits_{i = 1}^n \Big(t_i - y(x_i)\Big) x_{i,k} \\ \end{split}\]
Per cercare di controllare eventuali problemi di overfitting è possibile introdurre un fattore di regolarizzazione. In tal caso si dovrebbe calcolare il nuovo gradiente, che tiene conto di questo fattore di regolarizzazione, per poi effettuare una nuova ascesa del gradiente.
3 Newton-Raphson Method
Un altro metodo che ci permette di calcolare il punto in cui il la log-likelihood \(l(\mathbf{w} | \mathbf{X}, \mathbf{t})\) è massimizzata prende il nome di Newton-Raphson algorithm.
Data una funzione \(f: \mathbb{R} \to \mathbb{R}\), l'algoritmo trova una radice \(z \in \mathbb{R}\) di \(f\) tale che \(f(z) = 0\) tramite una sequenza di iterazioni che partono da un valore base \(z_0\) e che utilizzano la seguente regola di update
\[z_{i+1} = z_i - \frac{f(z_i)}{f^{'}(z_i)}\]
Ad ogni iterazione l'algoritmo approssima \(f\) utilizzando la retta tangente a \(f\) nel punto \((z_i, f(z_i))\), e definisce il nuovo valore \(z_{i+1}\) come il valore in cui la retta interseca l'asse delle \(x\).
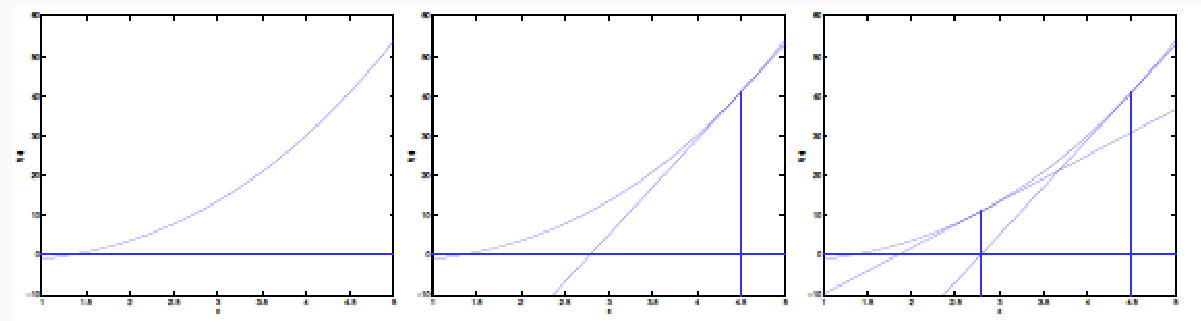
Questo metodo può essere esteso per calcolare i punti di massimo/minimo di una funzione andando a calcolare i punti in cui la derivata della funzione si annulla. Per questo secondo utilizzo la regola di update viene modificata come segue
\[z_{i+1} = z_i - \frac{f^{'}(z_i)}{f^{''}(z_i)}\]
Per poter utilizzare il metodo di Netwon-Raphson lo dobbiamo prima estendere al caso multivariato. Questo può essere fatto in modo abbastanza intuitivo andando a sostituire alla derivata prima il gradiente, e alla derivata seconda la matrice Hessiana.
Ricordiamo a tale fine che la Hessiam matrix \(\mathbf{H}\) (matrice Hessiana) contiene tutti i modi in cui poter effettuare la derivata seconda, ed è così definita
\[\mathbf{H}_{i,j}(f) = \frac{\partial^2 f}{\partial w_i \partial w_j}\]
La regola di update diventa quindi
\[\mathbf{w}^{(i+1)} = \mathbf{w}^{(i)} - \Big(\mathbf{H}(f) \Big|_{\mathbf{w}^{(i)}} \Big)^{-1} \cdot \frac{\partial f}{\partial \mathbf{w}} \Big|_{\mathbf{w}^{(i)}}\]
Osservazione: L'applicazione del metodo di Netwon-Raphson non sempre ci porta in un punto di massimo, ma ci potrebbe anche portare in un punto di sella o in un punto di minimo. Per discriminare queste situazioni si deve verificare se la matrice hassiana calcolata per il vettore che fa annullare il gradiente è def. positiva, def. negativa o nessuna delle due.
3.1 Linear Regression
Ricordando che nella regressione lineare la funzione da minimizzare era la seguente
\[E(\mathbf{w}) = \frac12 \sum\limits_{i = 1}^n (y_i - t_i)^2 = \frac12 \sum\limits_{i = 1}^n (\mathbf{w}^T \overline{x}_i - t_i)^2\]
applicando il metodo di Netwon-Raphson e ricordando che \(\mathbf{y} = \overline{\mathbf{X}} \mathbf{W}\), otteniamo che il gradiente può essere espresso come segue
\[\begin{split} \frac{\partial E}{\partial \mathbf{w}} &= \sum\limits_{i = 1}^n (y_i - t_i)\overline{x}_i \\ &= \overline{\mathbf{X}}^T (\mathbf{y} - \mathbf{t}) \\ &= \overline{\mathbf{X}}^T \mathbf{y} - \overline{\mathbf{X}}^T \mathbf{t} \\ &= \overline{\mathbf{X}}^T \overline{\mathbf{X}} \mathbf{w} - \overline{\mathbf{X}}^T \mathbf{t} \\ \end{split}\]
mentre la matrice hessiana è data da
\[\mathbf{H} = \frac{\partial}{\partial \mathbf{w}} \frac{\partial E}{\partial \mathbf{w}} = \sum\limits_{i = 1}^n \overline{x}_i \overline{x}_i^T = \overline{\mathbf{X}}^T \overline{\mathbf{X}}\]
La regola di update del metodo è quindi descritta come segue
\[\begin{split} \mathbf{w}^{(i+1)} &= \mathbf{w}^{(i)} - (\overline{\mathbf{X}}^T\overline{\mathbf{X}})^{-1}(\overline{\mathbf{X}}^T\overline{\mathbf{X}} \mathbf{w}^{(i)} - \overline{\mathbf{X}}^T \mathbf{t}) \\ &= (\overline{\mathbf{X}}^T\overline{\mathbf{X}})^{-1} \overline{\mathbf{X}}^T \mathbf{t} \\ \end{split}\]
che è proprio l'espressione in forma chiusa dell'ottimo.
3.2 Logistic Regression
Nel caso della regressione logistica la funzione di costo è cross-entropy loss function, definita come segue
\[\begin{split} E(\mathbf{w}) = -l(\mathbf{w} | \mathbf{X}, \mathbf{t}) = -\sum\limits_{i = 1}^n\Big(t_i \log{y_i} + (1 - t_i)\log{(1 - y_i)}\Big) \end{split}\]
con \(y_i = \sigma(a_i)\) e \(a_i = w^T \overline{x}_i\).
Troviamo quindi la seguente formula per il gradiente
\[\frac{\partial E}{\partial \mathbf{w}} = - \frac{\partial l(\mathbf{w}|\mathbf{X}, \mathbf{t})}{\partial \mathbf{w}} = \sum\limits_{i = 1}^n (y_i - t_i) \overline{x}_i = \overline{\mathbf{X}}^T (\mathbf{y} - \mathbf{t})\]
e la seguente formula per la matrice hessiana
\[\mathbf{H} = \frac{\partial}{\partial \mathbf{w}} \frac{\partial E}{\partial \mathbf{w}} = \sum\limits_{i = 1}^n y_i(1 - y_i)\overline{x}_i \overline{x}_i^T = \overline{\mathbf{X}}^T \mathbf{Y} \overline{\mathbf{X}}\]
dove \(\mathbf{y}\) è il vettore delle predizioni tale che \(y_i = \sigma(a_i) = \sigma(\mathbf{w}^T \overline{x}_i)\), mentre \(\mathbf{Y}\) è una matrice diagonale \(n \times n\) tale che \(Y_{i,i} = y_i(1 - y_i)\).
Il passo di iterazione del modo è quindi
\[\mathbf{w}^{(i+1)} = \mathbf{w}^{(i)} - (\overline{\mathbf{X}}^T \mathbf{Y} \overline{\mathbf{X}})^{-1} \overline{\mathbf{X}}^T(\mathbf{y}^{(i)} - \mathbf{t})\]
4 Iterated Reweighted Least Squares
Consideriamo adesso l'estesione pesata della least square cost function, chiamata weighted least squares cost function, e definita come segue
\[\sum\limits_{i = 1}^n \psi_i (y_i - t_i)^2 = \sum\limits_{i = 1}^n \psi_i(\mathbf{w}^T \overline{x}_i - t_i)^2\]
L'idea è che i valori \(\psi_1, \ldots, \psi_n\) sono dei pesi che regolano il contributo della feature rispetto all'errore totale. La funzione least squares può essere ottenuta da questa ponendo \(\psi_i = 1\) per ogni \(i = 1,\ldots,n\).
È possibile dimostrare che se si vuole minimizzare questa funzione il punto ottimale è dato da
\[\mathbf{w} = (\overline{\mathbf{X}}^T \mathbf{\Psi} \overline{\mathbf{X}})^{-1} \overline{\mathbf{X}}^T \Psi \mathbf{t}\]
dove la matrice \(\mathbf{\Psi}\) è una matrice diagonale con \(\mathbf{\Psi}_{i,i} = \psi_i\).
È possibile vedere che l'update di \(\mathbf{w}^{(i)}\) che viene effettuata dal metodo di Netwon-Raphson può essere calcolata risolvendo una nuove istanza del weighted least square problem, settando \(\mathbf{w}^{(i+1)}\) alla soluzione ottenuta, e derivando i nuovi valori per \(\mathbf{\Psi} = \mathbf{Y}^{(i+1)}\) e \(\mathbf{t} = \mathbf{z}^{(i+1)}\). Questo metodo prende il nome di iterated reweighted least squares.