ML - 14 - Probabilistic Classification IV
Lecture Info
Date:
Lecturer: Giorgio Gambosi
Slides: (ml_06_probclass-slides.pdf)
In questa lezione abbiamo terminato la trattazione della classificazione probabilistica discutendo le relazioni tra GDA e logistic regression, estendo poi quest'ultima al caso multiclasse per ottenere la softmax regression. Abbiamo poi parlato della probit regression, che può essere utilizzato al posto della regressione logistica. Infine, abbiamo terminato la lezione discutendo di un approccio completamente bayesiano per derivare un modello di regressione logistica.
1 Logistic Regression and GDA
Assumere che \(P(x|C_1)\) e \(P(x|C_2)\) siano multivariate normali con la stessa matrice di covarianza \(\mathbf{\Sigma}\) ci permette di avere come distribuzione a posteriori \(P(C_1|x)\) una distribuzione logistica.
Il risultato inverso però non vale: infatti GDA utilizza ipotesi più forti rispetto alla regressione logistica. Più le ipotesi di normalità per le distribuzioni \(P(x|C_1)\) con la stessa covarianza e più GDA tende a fornire i migliori modelli per \(P(C_1|x)\).
Dato che la regressione logistica si basa su ipotesi più deboli di quelle utilizzate da GDA, è molto meno sensibile a situazioni in cui queste ipotesi risultano avere una correttezza limitata. Da questo ne consegue che la regressione logistica ci permette di avere modelli più robusti. In particolare, dato che \(P(C_i|x)\) è logistica sotto un insieme ampio di ipotesi riguardanti \(P(x|C_i)\), tipicamente permette di ottenere modelli migliori in tutti i casi, mentre utilizzando GDA la qualità del modello ottenuto dipende da quanto le ipotesi di normalità iniziali su \(P(x|C_i)\) sono rispettate.
2 Softmax Regression
Andiamo adesso a discutere l'estensione della regressione logistica al caso \(K > 2\), ovvero quando abbiamo più di due classi da classificare. A tale fine consideriamo la matrice \(\mathbf{W} = (\mathbf{w}_1, \ldots, \mathbf{w}_K)\) di size \((d + 1) \times K\) contenente i cofficienti del modello, dove \(\mathbf{w}_j\) è un vettore di dimensione \(d+1\) conenente i coefficienti utilizzati per la classe \(C_j\).
In questo caso la likelihood è definita utilizzando la funzione softmax per stimare le probabilità. Troviamo quindi,
\[P(\mathbf{T} | \mathbf{X}, \mathbf{W}) = \prod\limits_{i = 1}^n \prod\limits_{k = 1}^K P(C_k|x_i)^{t_{i,k}} = \prod\limits_{i = 1}^n \prod\limits_{k = 1}^K \Bigg( \frac{e^{\mathbf{w}_k^T \overline{x}_i}}{\sum_{r = 1}^K e^{\mathbf{w}_r^T \overline{x}_i}}\Bigg)^{t_{i,k}}\]
dove \(\mathbf{X}\) è la matrice delle features e \(\mathbf{T}\) è la matrice \(n \times K\) dove la riga \(i\) contiene la codifica 1-to-K di \(t_i\).
La log-likelihood è quindi
\[l(\mathbf{W}) = \sum\limits_{i = 1}^n \sum\limits_{k = 1}^K t_{i,k} \log{\Bigg(\frac{e^{w_k^T \overline{x}_i}}{\sum_{r = 1}^K e^{w_r^T \overline{x}_i}} \Bigg)}\]
mentre il gradiente è definito come segue
\[\frac{\partial l(\mathbf{W})}{\partial \mathbf{W}} = \Bigg(\frac{\partial l(\mathbf{W})}{\partial \mathbf{w}_1}, \ldots, \frac{\partial l(\mathbf{W})}{\partial \mathbf{w}_K}\Bigg)\]
2.1 Calcolo Gradiente
Per derivare \(\frac{\partial l(\mathbf{W})}{\partial \mathbf{w}_j}\) osserviamo che è possibile scrivere la log-likeliihod come segue
\[l(\mathbf{W}) = \sum\limits_{i = 1}^n \sum\limits_{k = 1}^K t_{i,k} \log{y_{i,k}}\]
con
\[\begin{split} y_{i,k} &= \frac{e^{a_{i,k}}}{\sum_{r = 1}^K e^{a_{i,r}}} \\ \\ a_{i,k} &= \mathbf{w}_k^T \overline{x}_i \\ \end{split}\]
per \(j, k = 1, \ldots, K\) e \(i = 1, \ldots, n\). Osserviamo quindi che per ogni \(i, j\) e \(k\) otteniamo
\[\begin{split} \frac{\partial a_{i,k}}{\partial \mathbf{w}_j} &= \frac{\partial \mathbf{w}_k^T \overline{x}_i}{\partial \mathbf{w}_j} = \begin{cases} \overline{x}_i \,\,\,\,,& j = k \\ \mathbf{0} \,\,\,\,\,\,,& j \neq k \\ \end{cases} \\ \\ \frac{\partial y_{i, k}}{\partial a_{i, j}} &= \begin{cases} y_{i,k}(1 - y_{i,k}) \,\,\,\,,& j = k \\ -y_{i,j} \cdot y_{i,k} \,\,\,\,\,\,\,\,\,\,,& j \neq k \\ \end{cases} \\ \end{split}\]
ovvero,
\[\frac{\partial y_{i,k}}{\partial \mathbf{w}_j} = \sum\limits_r \frac{\partial y_{i,k}}{\partial a_{i,r}} \frac{\partial a_{i,r}}{\partial \mathbf{w}_j} = \frac{\partial y_{i,k}}{\partial a_{i,j}} \frac{\partial a_{i,j}}{\partial \mathbf{w}_j} = \frac{\partial y_{i,k}}{\partial a_{i,j}} \overline{\mathbf{x}}_i = \begin{cases} y_{i,k} ( 1 - y_{i,k}) \overline{x}_i \,\,\,\,,& j = k \\ -y_{i,j} \cdot y_{i,k} \cdot \overline{x}_i \,\,\,\,,& j \neq k \\ \end{cases}\]
e quindi,
\[\frac{\partial l(\mathbf{W})}{\partial \mathbf{w}_j} = \ldots = \sum\limits_{i = 1}^n (t_{i,j} - y_{i,j}) \overline{x}_i\]
Notiamo come il gradiente ottenuto ha la stessa struttura che abbiamo già visto sia nel caso della regressione lineare e sia nel caso della regressione logistica.
3 Probit Regression
La probit regressione viene utilizzata a volte al posto della regressione logistica e fa riferimento alla distribuzione normale. Ricordiamo che in un GLM abbiamo che
\[P(C_1 | x) = f(\mathbf{w}^T \overline{x})\]
dove \(f\) è detta funzione di attivazione. (sigmoide nel caso della regressione logistica).
3.1 Stochastic Treshold Model
La regressione probit è ottenuta applicando un modello più generale che prende il nome di stochastic treshold model (modello stocastico a soglia), che funziona nel seguente modo:
Si assume una distribuzione di probabilità \(\pi(\theta)\) e si considera \(\Pi(\theta)\) la corrispondente distribuzione cumulativa di probabilità, ovvero tale che \(\Pi(z) = \pi(\theta < z)\).
Siano \(\mathbf{w}\) i coefficienti del modello. Per classificare un elemento \(\mathbf{x}\) si effettua una combinazione lineare \(a_i = \mathbf{w}^T \overline{\mathbf{x}}\).
In un modello di questo tipo per definizione si ha
\[P(C_1|\mathbf{x}) = \Pi(\mathbf{w}^T \overline{\mathbf{x}})\]
ovvero \(P(C_1|\mathbf{x})\) corrisponde alla probabilità che un valore estratto a caso da \(\pi(\theta)\) è minore di \(\mathbf{w}^T \overline{\mathbf{x}}\).
In un modello del genere quindi la funzione di attivazione è ottenuta dalla funzione cumulativa
\[f(a) = \int\limits_{-\infty}^{\mathbf{w}^T \overline{\mathbf{x}}} \pi(\theta) \,\,\, d \theta\]
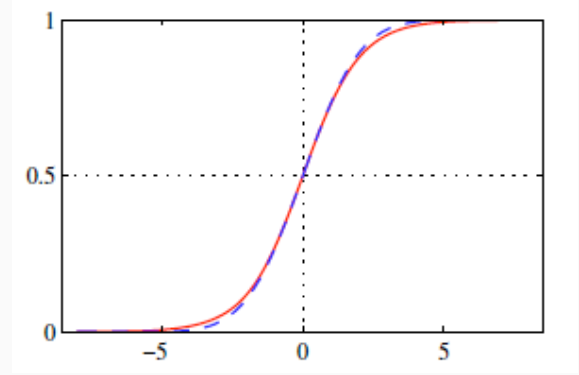
3.2 Probit Activation Function
La regessione probit è ottenuta nel momento in cui si assume che \(\pi(\theta)\) è una normale. La probit activation function è quindi data da
\[\Phi(a) = \int\limits_{-\infty}^a \frac{1}{\sqrt{2 \pi}} e^{-\frac{\theta^2}{2}} d \theta\]
Da notare che \(\Phi(a)\) è una funzione monotona crescente, con \(0 < \Phi(a) < 1\).
4 Bayesian Logistic Regression
Andiamo adesso ad utilizzare un approccio completamente bayesiano per derivare un modello di regressione logica.
Ricordiamo che in un approccio completamente bayesiano al posto di selezionare il miglior modello tra tutti quelli possibili, si effettua una operazione di media tra le probabilità a posteriori di tutti i possibili modelli al fine di fornire una distribuzione predittiva.
In generale quindi troviamo la seguente situazione
\[P(C_1 | x, \mathbf{X}, \mathbf{t}) \int P(C_1|x, \mathbf{w}) \cdot P(\mathbf{w} | \mathbf{X}, \mathbf{t}) \,\,\, d \mathbf{w}\]
Nel nostro caso particolare dato che vogliamo effettuare una regressione logistica otteniamo la seguente formula
\[P(C_1 | x, \mathbf{X}, \mathbf{t}) \int \sigma(\mathbf{w}^T \overline{\mathbf{x}}) \cdot P(\mathbf{w} | \mathbf{X}, \mathbf{t}) \,\,\, d \mathbf{w}\]
Utilizzando questo approccio quindi in qualche modo dobbiamo risolvere l'integrale mostrato prima, e in particolare necessitiamo di poter valutare la distribuzione a posteriori \(P(\mathbf{w} | \mathbf{X}, \mathbf{t})\).
4.1 Computing Posterior
Applicando la regola di Bayes otteniamo
\[P(\mathbf{w} | \mathbf{X}, \mathbf{t}) = \frac{P(\mathbf{t} | \mathbf{X}, \mathbf{w}) P(\mathbf{w})}{P(\mathbf{t} | \mathbf{X})} = \frac{P(\mathbf{t} | \mathbf{X}, \mathbf{w}) P(\mathbf{w})}{\int P(\mathbf{t} | \mathbf{X}, \mathbf{w}^{'}) P(\mathbf{w}^{'}) \,\,\, d \mathbf{w}^{'}}\]
dove la likelihood è data da
\[P(\mathbf{t} | \mathbf{X}, \mathbf{w}) = \prod\limits_{i = 1}^n P(t_i | x_i, \mathbf{w})\]
con
\[P(t_i | x_i, \mathbf{w}) = \begin{cases} \sigma(\mathbf{w}^T \overline{x}) \,\,\,\,&,& t_i = 1 \\ 1 - \sigma(\mathbf{w}^T \overline{x}) \,\,\,\,&,& t_i = 0 \\ \end{cases}\]
Un modo alternativo più compatto di descrivere la likelihood come al solito è il seguente
\[P(\mathbf{t} | \mathbf{X}, \mathbf{w}) = \prod\limits_{i = 1}^n \sigma(\mathbf{w}^T \overline{x})^{t_i} \Big(1 - \sigma(\mathbf{w}^T \overline{x}) \Big)^{1 - t_i}\]
e quindi
\[P(\mathbf{w} | \mathbf{X}, \mathbf{t}) = \frac{P(\mathbf{w}) \cdot \prod\limits_{i = 1}^n \sigma(\mathbf{w}^T \overline{x})^{t_i} \Big(1 - \sigma(\mathbf{w}^T \overline{x}) \Big)^{1 - t_i}}{Z}\]
dove \(Z\) è un fattore di normalizzazione
\[Z = \int P(\mathbf{w}) \cdot \prod\limits_{i = 1}^n \sigma(\mathbf{w}^T \overline{X})^{t_i}\Big(1 - \sigma(\mathbf{w}^T \overline{x})\Big)^{1 - t_i} \,\,\,\, d \mathbf{w}\]
Osservazione: Notiamo che fino a questo momento non è stati mai necessario calcolare il fattore di normalizzazione \(Z\), in quanto erevamo sempre solo interessati al modello \(\mathbf{w}\) che massimizzava la probaiblità a posteriori, e dato che il fattore di normalizzazione era uguale per ogni modello possibile lo potevamo semplicemente ignorare. In questo caso però dobbiamo stimare il valore effettivo di queste probabilità, e quindi dobbiamo effettivamente calcolare o stimare questo valore \(Z\).
Dato però che \(Z\) è difficile da calcolare, la cosa migliore che possiamo fare è evalutare il nominatore, che sarà proporzionale alla probabilità desiderata \(P(\mathbf{w} | \mathbf{X}, \mathbf{t})\) tramite un ignoto fattore di proporzionalità.
\[g(\mathbf{w}; \mathbf{X}, \mathbf{t}) = P(\mathbf{w}) \cdot \prod\limits_{i = 1}^n \sigma(\mathbf{w}^T \overline{x})^{t_i} \Big(1 - \sigma(\mathbf{w}^T \overline{x}) \Big)^{1 - t_i}\]
4.2 Managing Intractability
In generale ci sono varie strade che ci permettono di gestire le difficoltà computazionali relative all'utilizzo di un approccio completamente bayesiano. Tra queste troviamo
Maxium a Posteriori (MAP): Trovare un singolo valore di \(\mathbf{w}\) che massimizza \(P(\mathbf{w} | \mathbf{X}, \mathbf{t})\). Questo equivale a trovare il valore di \(\mathbf{w}\) che massimizza \(g(\mathbf{w} ; \mathbf{X}, \mathbf{t})\).
Variational approach: Si approssima \(P(\mathbf{w} | \mathbf{X}, \mathbf{t})\) con qualche altra densità di probabilità che sia abbastanza "simile" a quella di partenza ma che però può essere trattata analiticamente. In questo contesto la "similarità" è misurata tramite la KL-divergence.
Montecarlo approach: Si procede stimando numericamente la distribuzione \(P(\mathbf{w} | \mathbf{X}, \mathbf{t})\) utilizzando un qualche algoritmo che genera dei valori che seguono proprio la distribuzione che voglio stimare.