ML - 16 - Non Parametric Models
Lecture Info
Date:
Lecturer: Giorgio Gambosi
Slides: (ml_08_nonparam-slides.pdf)
In questa lezione abbiamo ripassato brevemente i metodi parametrici per effettuare la classificazione probabilistica. Abbiamo poi introdotto un metodo alternativo per fare classificazione tramte i metodi non parametrici e abbiamo mostrato tre particolari metodi di questo tipo: gli istogrammi, le parzen windows e il k-nearest neighbors.
1 Parametric Approach
Per introdurre i modelli non parametrici ricordiamo che tutti gli approcci per effettuare la classificazione probabilistica fanno riferimento a una qualche distribuzione di probabilità stimata a partire dal training set. Questo può avvenire in due modi diversi:
Modello discriminativo: In questo caso stimiamo la probabilità a posteriori della classe dato l'elemento, ovvero \(P(C_k|x)\) per ogni classe \(C_k\). All'elemento \(x\) è poi associata (tipicamente) la classe \(C_i\) che massimizza tale probabilità, ovvero tale che
\[i = \underset{k}{\text{argmax}} P(C_k|x)\]
Modello generativo: In quest'altro caso stimiamo sia la probabilità inversa, ovvero \(P(x|C_k)\) che la prior probability della classe \(P(C_k)\) per ogni classe \(C_k\). Applicando la regola di Bayes infatti tramite queste due probabilità siamo in grado di calcolare (a parte un fattore che non dipende dalla classe) la probabilità a posteriori \(P(C_k|x)\). Nuovamente, all'elemento \(x\) è poi (tipicamente) assegnata la classe che massimizza tale probabilità
\[i = \underset{k}{\text{argmax}} P(x|C_k) \cdot P(C_k)\]
In entrambi questi approccio abbiamo sempre assunto di conoscere il tipo di distribuzione di probabilità con cui avevamo a che fare. Così facendo infatti riusciamo a capire quali erano i coefficienti che dovevano essere derivati. Ad esempio,
(Discriminative, Softmax): Si assume che \(P(C_k|x)\) del tipo
\[\frac{e^{\mathbf{w}_k^T \overline{x}}}{\sum_ie^{\mathbf{w}_i^T}\overline{x}}\]
(Generative, GDA): Si assume che \(P(x|C_k)\) è una normale della forma
\[\mathcal{N}(x|\mu_k, \Sigma_k)\]
1.1 Estimating Parameters
Per stimare questi parametri abbiamo poi utilizzato diversi approcci:
1.1.1 Maximum Likelihood (ML)
Nel caso discriminativo consideriamo i coefficienti che massimizzano la likelihood del target
\[\mathbf{w}^{\text{ML}} = \underset{k}{\text{argmax}} P(\mathbf{t} | \mathbf{X}, \mathbf{w})\]
e la predizione è quindi data da
\[i = \underset{k}{\text{argmax}} \,\,\, P(C_k | \mathbf{x}, \mathbf{w}^{\text{ML}})\]
Nel caso generativo invece per ogni classe \(C_k\) massimizziamo la likelihood del sottoinsieme \(\mathbf{X}_k\) di elementi appartenenti alla classe \(C_k\)
\[\theta_k^{\text{ML}} = \underset{\theta}{\text{argmax}} \,\,\, P(\mathbf{X}_k | \theta_k)\]
e la predizione è data da
\[i = \underset{k}{\text{argmax}} \,\,\, P(\mathbf{x} | \theta_k^{\text{ML}}) \cdot P(C_k)\]
1.1.2 Maximum a Posteriori (MAP)
Nel caso discriminativo consideriamo il modello che massimizza la probabilità a posteriori rispetto al training set
\[\mathbf{w}^{\text{MAP}} = \underset{k}{\text{argmax}} \,\,\, P(\mathbf{w} | \mathbf{X}, \mathbf{t})\]
e la predizione è data da
\[i = \underset{k}{\text{argmax}} \,\,\, P(C_k | \mathbf{x}, \mathbf{w}^{\text{MAP}})\]
Nel caso generativo invece per ogni classe \(C_k\), si sceglie il modello che massimizza la probabilità a posteriori rispetto agli elementi di quella classe
\[\theta_k^{\text{MAP}} = \underset{\theta_k}{\text{argmax}} \,\,\, P(\theta_k | \mathbf{X}_k)\]
mentre la predizione è ottenuta da
\[i = \underset{k}{\text{argmax}} \,\,\, P(x|\theta_k^{\text{MAP}} \cdot P(C_k)\]
1.2 Bayesian Approach
In quest'altro caso la distribuzione predittiva veniva direttamente espressa dalla media rispetto a tutti i possibili modelli, dove la predizione di ogni modello è pesata in funzione della verosimiglianza, ovvero di quanto il modello rispecchia i dati in input.
\[P(C_k | \mathbf{x}, \mathbf{X}, \mathbf{t}) = \int_{\mathbf{w}} P(C_k | \mathbf{x}, \mathbf{w}) \cdot P(\mathbf{w} | \mathbf{X}, \mathbf{t}) \,\,\, d \mathbf{w}\]
2 Non Parametric Approach
Un approccio diverso da quelli visti fino ad ora è chiamato non parametri approach, ovvero approccio non parametrico.
In questo tipo di approccio non si assume alcun tipo di conoscenza a priori sulle distribuzioni di probabilità che descrivono i dati. Dato che non si assume nulla, le probabilità \(P(x|C_i)\) non sono calcolate facendo riferimento a qualche modello, ma sono calcolate direttamente dai dati. In altre parole, non utilizziamo più dei modelli probabilistici come descrizioni sintetiche del training set \(\mathbf{X}, \mathbf{t}\).
Questi modelli sono detti non parametri proprio per l'assenza di parametri. In realtà, cambiando leggermente punto di vista, potremmo pensare che questi modelli hanno un numero indefinito (unbounded) di parametri.
3 Histograms
Un primo approccio elementare di tipo non parametrico consiste nell'utilizzo di istogrammi.
L'idea è quelal di partizionare il dominio dei possibili valori in un certo numero \(m\) di intervalli, chiamati bins. La pobabilità \(P_x\) che un nuovo elemento appartiene al bin contenente l'elemento \(x\) è stimata come segue
\[P_x \approx \frac{n(x)}{n}\]
dove \(n(x)\) è il numero di elementi contenuti nel bin di \(x\).
La densità di probabilità \(p_H(x)\) nell'intervallo corrispondente al bin che contiene l'elemento \(x\) viene stimata come il rapporto tra la probabilità \(P_x\) e l'ampiezza dell'intervallo considerato \(\Delta(x)\)
\[p_H(x) = \frac{P_x}{\Delta(x)} = \frac{\frac{n(x)}{n}}{\Delta(x)} = \frac{n(x)}{N \Delta(x)}\]
Tipicamente l'ampiezza dei bins è una costante \(\Delta\).
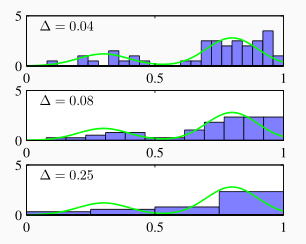
L'utilizzo degli istogrammi crea vari problemi. Il maggiore di questi è che variando il punto iniziale in cui conto la suddivisione di intervalli in bins, ciascun bin sarà posizionato diversamente e quindi un punto di un certo valore può avere probabilità diverse a seconda di dove inizio la suddivisione.
4 Kernel Density Estimators
Per cercare di colmare le lacune degli istogrammi sono stati introdotti approcci non parametri più robusti. Tra questi troviamo la teoria dei kernel density estimators.
In questo approccio non andiamo a suddividere il dominio a priori in bins, ma consideriamo per ogni elemento \(x\) un intorno di una certa dimensione. In particolare, partendo dall'elemento \(x\), consideriamo una regione \(\mathcal{R}(x)\) e stimiamo la probabilità \(P_x\) che un nuovo elemento cade in questa regione nel seguente modo
\[P_x = \int_{\mathcal{R}(x)} p(\mathbf{z}) \,\, d \mathbf{z}\]
dove per definizione \(p(\mathbf{z})\) è la densità di probabilità che vogliamo andare a stimare.
Dati \(n\) elementi \(x_1, x_2, \ldots, x_n\), la probabilità che \(k\) tra questi si trovano nella regione \(\mathcal{R}(x)\) è data dalla distribuzione binomiale
\[p(k) = \binom{n}{k}P_x^k (1 - P_x)^{n-k} = \frac{n!}{k!(n - k)!} \cdot P_x^k (1 - P_x)^{n-k}\]
Dato che in una distribuzione binomiale media e varianza sono calcolate come segue
\[\begin{split} \mathbb{E}[k] &= n P_x \\ \\ \sigma^2_k &= n P_x (1 - P_x) \\ \end{split}\]
se consideriamo la frazione \(r = k/n\) degli elementi che cadono nella regione rispetto a tutti gli altri elementi otteniamo che
\[\begin{split} \mathbb{E}[r] &= \frac{1}{n} \cdot \mathbb{E}[k] = P_x \\ \\ \sigma_r^2 &= \frac{1}{n^2} \sigma_k^2 = \frac{P_x(1 - P_x)}{n} \end{split}\]
Questo significa che al crescere di \(n \to \infty\) la varianza tende a \(0\) e quindi il rapporto \(r\) tende a \(\mathbb{E}[r] = P_x\). In particolare quindi assumiamo
\[r = \frac{k}{n} \approx P_x\]
dove \(r\) può essere calcolata dal training set una volta che ho definito la mia regione \(\mathcal{R}(x)\). Assumendo poi che il volume della regione \(\mathcal{R}(x)\) sia abbastanza piccolo, otteniamo che la densità \(p(x)\) è quasi costante nella regione, e quindi
\[P_x = \int_{\mathcal{R}(x)} p(\mathbf{z}) \,\, d \mathbf{z}) \approx p(x) \cdot V\]
dove \(V\) è il volume di \(\mathcal{R}(x)\). Da questo e dal fatto che \(P_x \approx k/n\) ne consegue che
\[p(x) \approx \frac{k}{n V}\]
A questo punto per utilizzare la relazione appena ottenuta in modo tale da calcolare \(p(x)\) per ogni \(x\) ci sono due strade diverse:
Kernel density estimation: Si fissa \(V\) e si deriva \(k\) dai dati.
K-nearest neighbor: Si fissa \(k\) e si deriva \(V\) dai dati.
È possibile dimostrare che in entrambi questi approcci, sotto ragionevoli ipotesi, le stime tendono a convergere al vero valore di densità \(p(x)\) per \(n \to \infty\).
4.1 Parzen Windows
Consideriamo adesso il primo approccio. In questo approccio dobbiamo definire una regione associata la punto \(x\). L'idea è quella di definire un ipercubo centrato su \(x\) con lato di lunghezza \(h\) e volume \(h^d\) (lavorando in \(d\) dimensioni).
Per rappresentare il numero elementi che finiscono in questi ipercubi si definisce una funzione kernel \(k(\mathbf{z})\), detta Parzen window. Inizialmente la funzione è definita per ocntare il numero di elementi che entrano nell'ipercubo di lato \(1\) centranto nell'origine \(\mathbf{0}\)
\[k(\mathbf{z}) = \begin{cases} 1 \,\,\,,\,\,\,& |z_i| \leq 1/2, \,\, i = 1,\ldots, d \\ 0 \,\,\,,\,\,\,& \text{altrimenti} \\ \end{cases}\]
a questo punto notiamo che un punto \(x^{'}\) si trova nell'ipercubo di lato \(h\) centrato in \(x\) se e solo se
\[k\Big( \frac{x - x^{'}}{h}\Big) = 1\]
Il numero di elementi nell'ipercubo centrato in \(x\) con lato \(h\) è quindi
\[K = \sum\limits_{i = 1}^n k\Big( \frac{x - x_i}{h}\Big)\]
La densità stimata è quindi data da
\[p(x) = \frac{1}{nV} \cdot k = \frac{1}{n h^d} \cdot \sum\limits_{i = 1}^n k\Big( \frac{x - x_i}{h}\Big)\]
dato poi che \(k(\mathbf{z}) \geq 0\) e \(\int k(\mathbf{z}) \,\,\, d \, \mathbf{z} = 1\) ne deriva che
\[\begin{split} k\Big(\frac{x - x_i}{h}\Big) &\geq 0 \\ \\ \int k\Big(\frac{x - x_i}{h}\Big) \,\, d \, x &= h^d \\ \end{split}\]
da questo segue che \(p_n(x)\) è una densità di probabilità. Infatti
\[p(x) = \frac{1}{n} \sum\limits_{i = 1}^n \frac{1}{h^d} k\Big(\frac{x - x_i}{h}\Big) \geq 0\]
e inoltre
\[\begin{split} \int p(x) \,\, dx &= \int \frac{1}{n} \sum\limits_{i = 1}^n \frac{1}{h^d}k\Big(\frac{x - x_i}{h}\Big) \,\,\, d x \\ &= \frac{1}{n h^d} \int \sum\limits_{i = 1}^n k\Big(\frac{x - x_i}{h}\Big) \,\,\, d x \\ &= \frac{1}{n h^d} \sum\limits_{i = 1}^n \int k\Big(\frac{x - x_i}{h}\Big) \,\,\, d x \\ &= \frac{1}{n h^d} \cdot n h^d \\ &= 1 \end{split}\]
Notiamo come la window size h è un effetto rilevante sulla stima ottenuta. In particolare, all'aumentare di \(h\) la densità stimata tende ad essere più uniforme, e man mano che diminuisco il valore di \(h\) avrò una densità sempre più frastagliata.
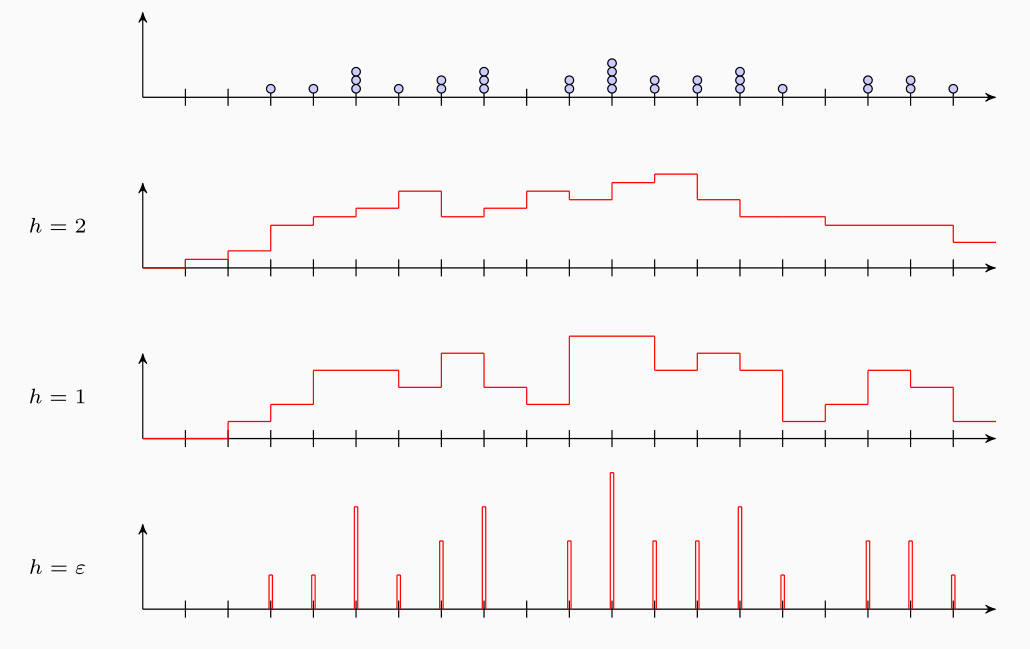
4.1.1 Drawbacks
Alcuni problemi di questo approccio sono i seguenti:
Nei valori stimati ci sono delle discontinuità, nel senso che cambiando di poco l'elemento la probabilità stimata potrebbe cambiare in modo sostanziale.
Gli elementi in una regione centrata su \(x\) hanno tutti un peso uniforme, ovvero non prendiamo in considerazione la loro distanza da \(x\).
4.2 Smooth Kernel Functions
Per risolvere questi problemi posso cambiare leggermente l'approccio descritto in precedenza. L'idea infatti è che al posto di considerare delle funzioni definite "a gradino", posso definire delle funzioni smooth che variano in modo continuo rispetto alla distanza dal punto \(x\) considerato.
Per fare questo si utilizzano delle smooth kernel functions \(\kappa_h(u)\) che assumono valori tanto maggiori quanto vicino il punto è all'origine considerata. Caratteristiche tipiche che vengono assunte per queste funzioni sono le seguenti:
\[\begin{split} \int \kappa_h(x) \,\,\, dx = 1 \\ \\ \int x \cdot \kappa_h(x) \,\,\, dx = 0 \\ \\ \int x^2 \cdot \kappa_h(x) \,\,\, dx = 0 \\ \end{split}\]
Tipicamente queste funzioni kernel sono basate su smooth radial functions, ovvero funzioni della distanza di un punto dall'origine. Alcuni esempi:
Gaussian (unlimited support)
\[\kappa(u) = \frac{1}{\sqrt{2 \pi \sigma}}e^{-\frac12 \frac{\mu^2}{\sigma^2}}\]
Epanechnikov (limited support, ovvero diversa da \(0\) solamente per \(u \in [-\frac12, \frac12]\))
\[\kappa(u) = 3 \Big(\frac12 - u^2 \Big) \;\;\;\; |u| \leq \frac12\]

Così facendo il valore della densità stimato (caso unidimensionale) diventa
\[p(x) = \frac{1}{n h} \sum\limits_{i = 1}^n \kappa\Big(\frac{x - x_i}{h}\Big) = \frac{1}{n} \sum\limits_{i = 1}^n \kappa_h (x - x_i)\]
4.2.1 Gaussian Kernel Examples
Notiamo che al variare di \(h\) la situazione varia, esattamente come nel caso precedente.
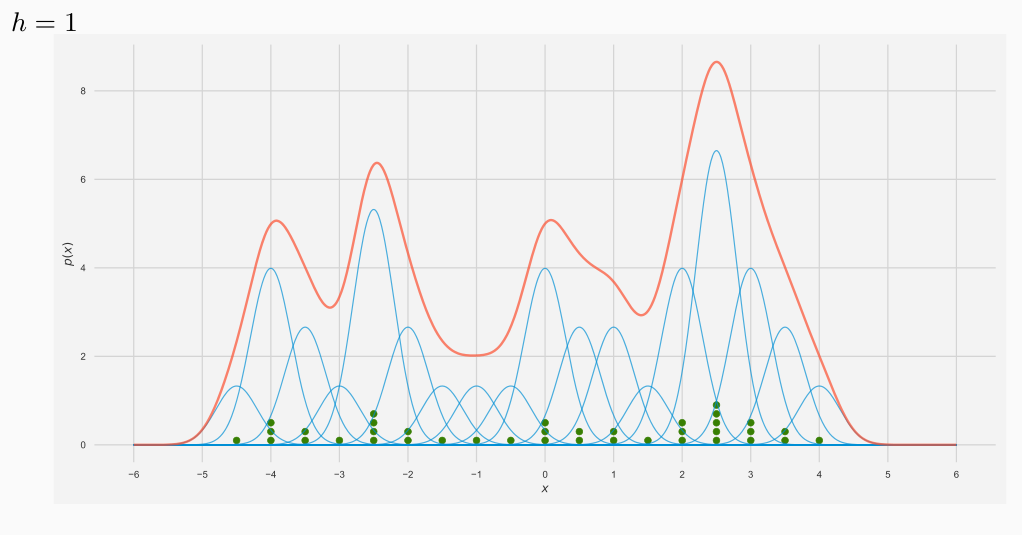
Ognuna delle linee azzurre rappresentano la funzione kernel centrata su ogni posizione in cui ci sono punti. Notiamo che hanno tutte la stessa forma ma differiscono solo per l'altezza, che dipende dal numero di elementi che cadono nel punto considerato.
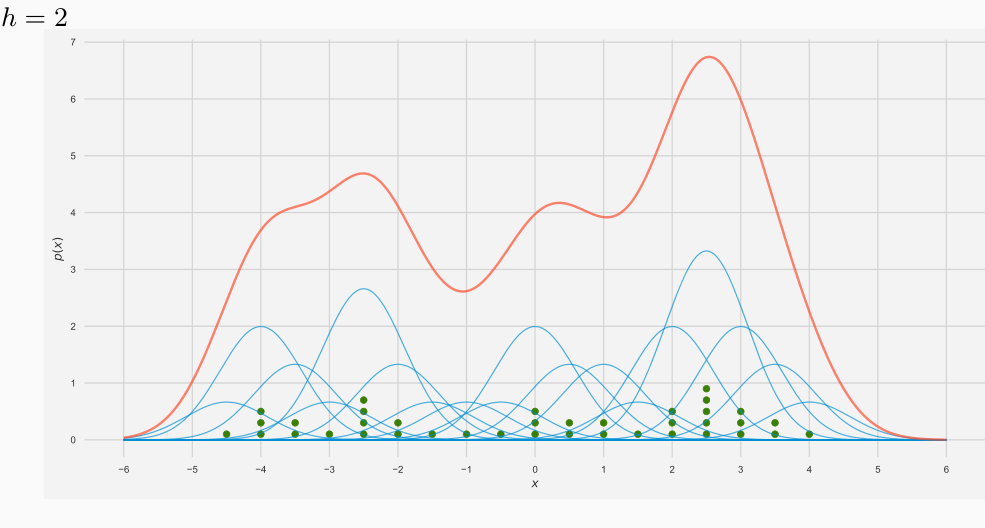
La linea rossa invece rappresenta la stima della densità della distribuzione di probabilità che deriva dalla somma punto per punto di queste funzioni.
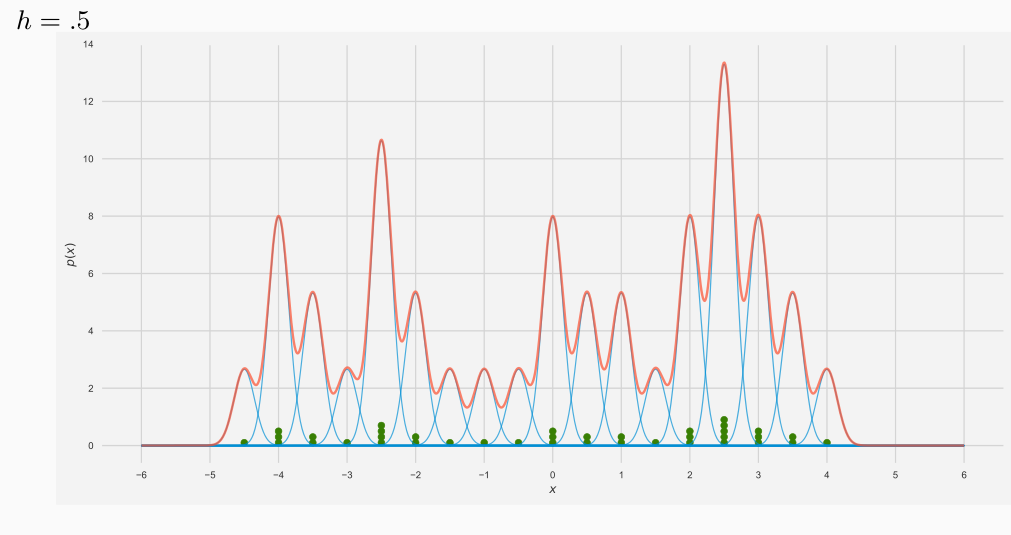
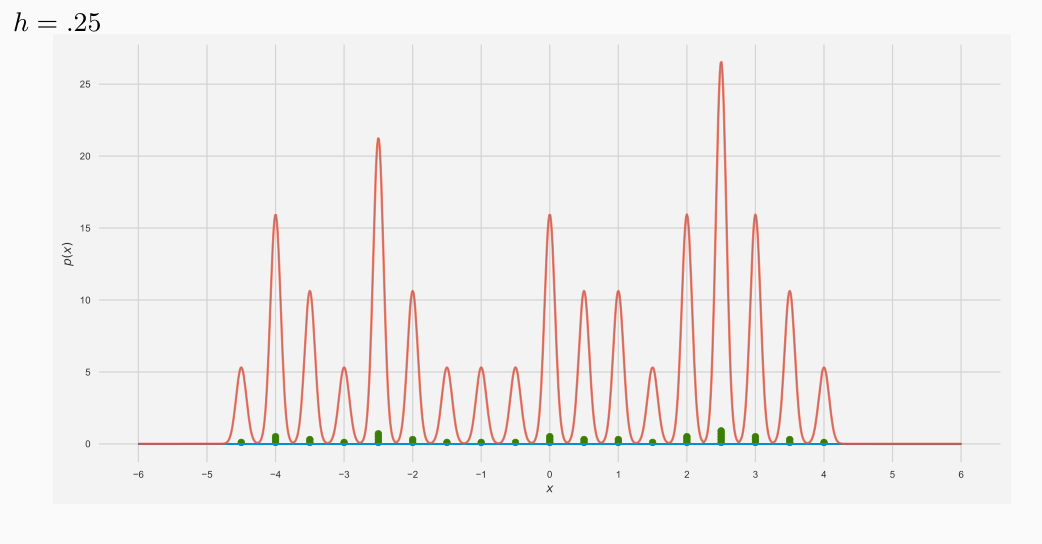
Al decrescere della finestra che sto considerando la funzione tende a diventare sempre più frastagliata.
4.3 Classification with Parzen Windows
Dato che le parzon windows ci permettono di stimare la densità \(p(x)\) per ogni elemento \(x\) dato un insieme di punti \(\mathbf{X}\), esse possono essere utilizzate per classificare l'elemento \(x\) andando a stimare la probaiblità \(P(x|C_k)\) per tutte le classi.
Applicando il tipico approccio del classificatore bayesiano otteniamo
\[\begin{split} \underset{i}{\text{argmax}} \,\,\, P(x|C_i) \cdot P(C_k) &= \underset{i}{\text{argmax}} \,\,\, \frac{1}{n_i h^d} \sum\limits_{i = 1}^{n_i} k\Big(\frac{x - x_i}{h}\Big) \cdot P(C_i) \\ &= \underset{i}{\text{argmax}} \,\,\, \frac{1}{n_i h^d} \sum\limits_{i = 1}^{n_i} k\Big(\frac{x - x_i}{h}\Big) \cdot \frac{n_i}{n} \\ &= \underset{i}{\text{argmax}} \,\,\, \frac{1}{n h^d} \sum\limits_{i = 1}^{n_i} k\Big(\frac{x - x_i}{h}\Big) \\ &= \underset{i}{\text{argmax}} \,\,\, \sum\limits_{i = 1}^{n_i} k\Big(\frac{x - x_i}{h}\Big) \\ \end{split}\]
ogni elemento viene quindi assegnato alal classe che contiene più punti (secondo il kernel scelto) nell'ipercubo con il lato lungo \(h\) centrato su \(x\).
Osservazione: Da un punto di vista computazionale a meno di fare specifiche ottimizzazioni per classificare ogni punto dovremmo andare a guardare tutti gli elementi del training set. Questa è una conseguenza del fatto che non abbiamo utilizzato nessuna descrizione sintetica del training set.
5 K-Nearest Neighbors (kNN)
L'approccio alternativo alla stima della densità di probabilità è tramite l'utilizzo del metodo kNN. In questo metodo fissiamo \(k\) e estendiamo la dimensione della regione intorno a \(x\) in modo tale da includere \(k\) elementi.
In questo approccio è più conveniente considerare delle ipersfere piuttosto che degli ipercubi
\[p(x) \approx \frac{k}{n V} = \frac{k}{n \cdot c_d \cdot r^d_k(x)}\]
dove,
\(c_d\) è il volume dell'ipersfera di \(d\) dimensioni con raggio unitario.
\(r_k^d(x)\) è la distanza da \(x\) al più vicino $k$-esimo elemento, ovvero è il raggio della più piccola ipersfera centrata in \(x\) che contiene \(k\) elementi.
5.1 Classification with kNN
L'idea dietro un classificatore di tipo kNN è la seguente: si considerano tutti gli elementi del training set e consideriamo i \(k\) elementi più vicini all'elemento che vogliamo classificare. La classificazione viene fatta assegnando il nuovo elemento alla classe che compare più frequentemente all'interno di questi \(k\) elementi.
Supponiamo quindi di voler stimare \(P(C_i|x)\) al fine di classificare \(x\). Per fare questo consideriamo quindi una ipersfera di volume \(V\) con centro \(x\) contenente \(k\) elementi del training set. Sia \(k_i\) il numero di elementi tra questi \(k\) che appartengono alla classe \(C_i\). Da quanto visto prima vale la seguente approssimazione
\[P(x|C_i) \approx \frac{k}{n_i V}\]
dove \(n_i\) sono gli elementi del training set che fanno parte della classe \(C_i\).
In modo analogo, la probabilità di \(x\), ovvero la probabilità di avere un elemento in quel punto all'interno del training set può essere stimata come segue
\[P(x) \approx \frac{k}{n V}\]
Mentre la distribuzione a priori è data da
\[P(C_i) = \frac{n_i}{n}\]
Applicando Bayes ottengo quindi
\[P(C_i|x) = \frac{P(x|C_i) \cdot P(C_i)}{P(x)} = \frac{\frac{k_i}{n_i \cdot V} \cdot \frac{n_i}{n}}{\frac{k}{nV}} = \frac{k_i}{k}\]
Questo significa che la frazione di elementi fra i \(k\) elementi che appartengono alla classe \(C_i\) ci permette di stimare il valore di probabilità di \(P(C_i|x)\).
La regola per effettuare la classificazione tramite kNN è molto semplice: un elemento è classificato basandoci sugli elementi più "simili" a lui nel training set. Per classificare \(x\) quindi si determinano i \(k\) elementi più "vicini" a \(x\) e assegnamo a \(x\) la classe di maggioranza tra questi. Per fare questo ovviamente necessitiamo di una metrice che ci permetta di misurare la similarità tra due elementi del training set.
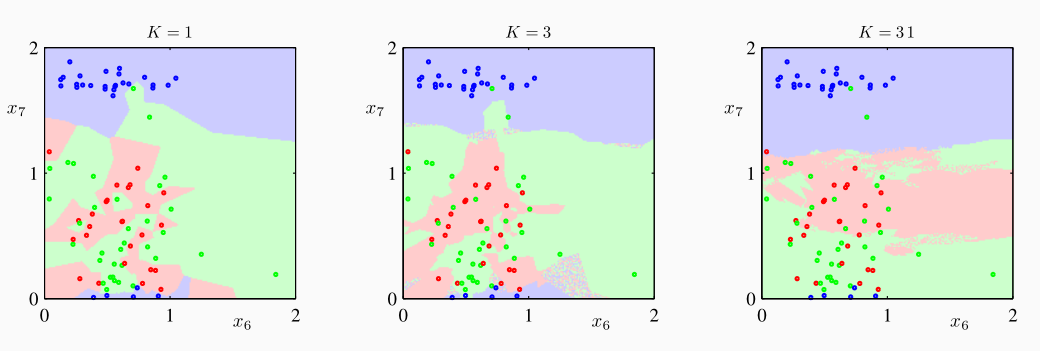
5.2 Performance
Anche se il classificatore kNN è molto semplice, riesce comunque ad avere ottime performance data una buona metrica per misurare la distanza e abbastanza dati classificati inizialmente. È possibile dimostrare infatti che kNN ottiene una 2 approssimazione dell'ottimo possibile per \(n \to \infty\).
Alcuni svantaggi di questo metodo invece sono i seguenti:
È soggetto alla curse of dimensionality, ovvero se il numero di dimensioni del training set è molto grande, dato un punto per riuscire a raggiungere i \(k\) punti più vicini potrebbe essere necessario arrivare ad una distanza molto elevata, andando perdere il concetto intuitivo di "distanza vicina".
Concettualmente per andare a classificare un elemento devo andare a considerare tutti i dati del training set.