ML - 18 - Gaussian Processes
Lecture Info
Date:
Lecturer: Giorgio Gambosi
Slides: (ml_09_gp-slides.pdf)
In questa lezione abbiamo introdotto i processi gaussiani e abbiamo discusso di come possono essere utilizzati in un contesto di regressione.
1 Partitions of Gaussian Distributions
Iniziamo ripassando qualche proprietà delle distribuzioni gaussiane multivariate.
Sia \(x = (x_1, \ldots, x_n)^T\) un vettore \(n\) dimensionale aleatorio, ovvero in cui \(x_i\) sono tutte v.a., e in particolare che segue una distribuzione gaussiana multivariata \(p(x)= \mathcal{N}(\mu, \mathbf{\Sigma})\).
Sia \(x = (x_A, x_B)\) una partizione delle componenti di \(x\) tali che
\[\begin{split} x_A &= (x_1, \ldots, x_r)^T \\ x_B &= (x_{r+1}, \ldots, x_n)^T \\ \end{split}\]
1.1 Marginal density
Notiamo quindi che le densità marginali \(P(x_A)\) e \(P(x_B)\) sono entrambi gaussiane con vettori media \(\mu_A\), \(\mu_B\) e matrici di covarianza \(\mathbf{\Sigma}_A\) e \(\mathbf{\Sigma}_B\) che possono essere ottenuti da \(\mu\) e \(\mathbf{\Sigma}\) osservando che
\[\begin{split} \mu &= (\mu_A, \,\, \mu_B)^T \\ \\ \mathbf{\Sigma} &= \begin{pmatrix} \mathbf{\Sigma}_A & \mathbf{\Sigma}_{AB} \\ \mathbf{\Sigma}_{AB} & \mathbf{\Sigma}_B \\ \end{pmatrix} \end{split}\]
Per ogni variabile \(x_i\) la media corrispondente quindi rimane immutata \(\mu_i\) e questo vale anche per la covarianza \(\sigma_{i,j}\) tra ogni coppia di varaibili \(x_i, x_j\) appartenenti alla stessa partizione.
1.2 Conditional Density
Anche le densità condizionali \(P(x_A | x_B)\) e \(P(x_B|x_A)\) sono gaussiane, con media
\[\begin{split} \mu_{A|B} &= \mu_A + \mathbf{\Sigma}_{AB} \mathbf{\Sigma}^{-1}_B(x_B - \mu_B) \\ \mu_{B|A} &= \mu_B + \mathbf{\Sigma}_{BA} \mathbf{\Sigma}^{-1}_A(x_A - \mu_A) \\ \end{split}\]
e matrice di covarianza
\[\begin{split} \mathbf{\Sigma}_{A|B} &= \mathbf{\Sigma}_A - \mathbf{\Sigma}_{AB} \mathbf{\Sigma}_B^{-1} \mathbf{\Sigma}_{BA} \\ \mathbf{\Sigma}_{B|A} &= \mathbf{\Sigma}_B - \mathbf{\Sigma}_{BA} \mathbf{\Sigma}_A^{-1} \mathbf{\Sigma}_{AB} \\ \end{split}\]
2 Distributions over Functions (Finite Domains)
Per introdurre i processi gaussiano consideriamo inizialmente il caso in cui abbiamo a che fare con funzioni definite su vettori di dimensioni finite.
Sia quindi \(\chi = (x_1, \ldots, x_m)\) un qualsiasi vettore di dimensione finita, e sia \(\mathcal{H}\) l'insieme delle funzioni da \(\chi\) a \(\mathbb{R}^m\). Una funzione \(f \in \mathcal{H}\) può essere descritta esplicitamente tramite un vettore che contiene l'insieme dei suoi valori rispetto a tutte le componenti del vettore \(\chi\), ovvero
\[f = (f(x_1), \ldots, f(x_m))\]
Dunque ogni vettore di reali \((y_1, \ldots, y_m)\) tale che \(f(x_i) = y_i\) può essere visto come una descrizione della funzione \(f \in \mathcal{H}\). Questo significa che l'insieme \(\mathcal{H}\) può essere messo in una corrispondenza biunivoca con l'insieme dei vettori in \(\mathbb{R}^m\), in quanto ciascuna funzione è descritta in modo univoco dall'insieme dei valori che la funzione assume nelle \(m\) componenti del vettore \(\chi\).
Consideriamo adesso una densità di probabilità \(p(x)\) definita sul dominio \(x \in \mathbb{R}^m\), ovvero su vettori reali \(m\) dimensionali. Per quanto detto prima, dato che ogni vettore rappresenta una funzione, il dominio su cui è definita questa densità può essere visto in due modi diversi:
Sia come l'insieme \(\mathbb{R}^m\) di vettori reali \(m\) dimensionali.
Sia come l'insieme delle funzioni \(f \in \mathcal{H}\).
2.1 Gaussian Distributions
Se assumiamo che \(p(x)\) (o, equivalentemente, \(p(f)\)), è una gaussiana multivariata centrata sullo \(\mathbf{0}\) e con matrice di covarianza diagonale \(\sigma^2 \mathbf{I}\), otteniamo
\[p(f) = \mathcal{N}(f | \mathbf{0}, \sigma^2 \mathbf{I}) = \prod\limits_{i = 1}^m \frac{1}{\sqrt{2 \pi} \sigma} e^{-\frac{f(x_i)^2}{2 \sigma^2}}\]
Possiamo quindi considerare questa probabilità come la prior distribution of functions, rispetto all'osservazione del valore assunto da una qualunque variabile \(x_j\), per \(1 \leq j \leq m\).
Assumiamo adesso che per qualche sottoinsieme \(I \subseteq \{1, \ldots, m\}\) abbiamo le osservazioni \(\mathbf{t}_I = \{t_j , \,\,\, j \in I\}\) dei valori delle variabili \(\mathbf{X}_I = \{x_j, \,\, j \in I\}\).
È quindi possibile parlare delle distribuzioni a posteriori \(p(f|\mathbf{X}_I)\), che è la distribuzione di probabilità tra tutte le possibili funzioni (o vettori casuali) assunto che per le variabili in \(\mathbf{X}_I\) conosco i valori associati dalla funzione. Per fare questo dobbiamo applicare, come al solito, la regola di Bayes
\[P(f|\mathbf{X}_I) \propto P(\mathbf{X}_I | f) \cdot P(f)\]
oltre alla distribuzione a priori quindi necessitiamo anche di un modello per la versomiglianza (likelihood). A tale fine si può assumere la tipica likelihood andando ad introdurre un fattore di noise \(\epsilon\) distribuito come una normale \(p(\epsilon) = \mathcal{N}(\epsilon | 0, \beta)\).
\[t_i = f(x_i) + \epsilon\]
Così facendo la distribuzione predittiva \(P(t_k|x_k, \mathbf{X}_I)\) per ogni altro \(x_k, k \not \in I\) può essere ottenuta nel seguente modo
\[P(t_k|x_k, \mathbf{X}_I) = \int P(t_k|f, x_k) \cdot P(f | \mathbf{X}_I) \,\, df\]
3 Gaussian Processes (Infinite Domains)
Consideriamo adesso il caso in cui il vettore \(\chi\) sia infinito, ovvero che dobbiamo gestire una collezione infinita di variabili aleatorie. L'infinito che stiamo trattando in questo caso è un infinito potenziale, nel senso che di volta in volta considereremo solo un certo insieme finito di v.a., con la caratteristica cruciale però che l'insieme di v.a. che consideriamo non è limitato a priori in nessun modo.
Estendendo le considerazione fatte prima, il ruolo delle distribuzioni multidimensionali viene assunto da un concetto più ampio noto con il nome di processo stocastico (stochastic processes). A tale fine introduciamo le seguenti definizioni:
Stochastic process: collezione di variabili aleatorie \(\{f(x): \,\, x \in \chi\}\) indicizzate da elementi presi da un qualche insieme \(\chi\) noto come index set.
Gaussian process: processo stocastico in cui ogni sottoinsieme finito di variabili random è distirbuito come una gaussiana multivariata.
I processi gaussiani sono essenzialmente un'estensione di distribuzioni gaussiane multivariate al caso in cui abbiamo a che fare con una collezione infinita di v.a. reali. In questo contesto i nostri vettori rappresentati da gaussiane multivariate al tendere della loro dimensione \(n \to \infty\) diventano processi gaussiani. Un altro modo per vedere i processi gaussiani è di considerarli come distribuzioni che non sono definite su dei vettori casuali ma su delle funzioni reali casuali.
Quando lavoriamo con un numero arbitrario e potenzialmente infinito di v.a. non possiamo più procedere come abbiamo fatto nel caso finito. Nel caso finito infatti per calcolare la distribuzione a priori abbiamo definito per ogni componente \(x_i\) del vettore \(\chi\) un valore di media e per ogni coppia di componenti \((x_i, x_j)\) un valore di covarianza.
Per definire correttamente un processo gaussiano e quindi per gestire questo infinito potenziale l'idea è quella di definire due funzioni che ci calcolano rispettivamente la media e la varianza per ogni componente del vettore \(\chi\). In particolare necessitiamo di:
Una funzione media \(m(x)\), che mappa ogni variabile \(x \in \chi\) al valore medio \(f(x)\) al variare di tutte le possibili funzioni \(f\).
Una funzione kernel \(\kappa(x_1, x_2)\) che mappa ogni coppia di variabili \((x_i, x_j) \in \chi^2\) al valore di covarianzda di \(f(x_1)\) e \(f(x_2)\) su tutte le funzioni \(f\).
In un processo gaussiano quindi il valore atteso di \(f(x)\) è fornito da una funzione \(m(x)\), mentre la covarianza è fornita da una funzione kernel \(\kappa(x_1, x_2)\). Definendo queste due funzioni ho definito un processo gaussiano con una specifica distribuzione di probabilità.
Dato un processo gaussiano \(\mathcal{GP}(m, \kappa)\), una funzione \(f\) estratta da tale processo (ovvero un vettore di elementi finito) può essere intuitivamente considerata come un vettore con tantissime dimensioni estratto da una multivariata gaussiana con tantissime dimensioni (potenzialmente infinite). Ogni dimensione della gaussiana corrisponde ad un elemento del dominio \(\chi\) e la corrispondente componente del vettore random rappresenta il valore \(f(x)\).
Utilizzando poi le proprietà di marginalizzazione delle gaussiane multivariate (discussa all'inizio di questa lezione) possiamo ottenere la densità corrispondente a qualsiasi insieme finito di variabili, dove tale densità risulta essere anch'essa una gaussiana multivariata.
Considerando un qualunque insieme finito \(\mathbf{X} = (x_1, \ldots, x_m)\) di \(\chi\), otteniamo che la distribuzione corrispondente all'insieme di v.a. \((f(x_1), \ldots, f(x_m))\) può essere vista come la marginalizzazione della distribuzione su vettori infiniti di variabili definite da \(\chi\). Tale distribuzione è gaussiana per le proprietà di gaussianità ed è data da
\[p(f(x_1), \ldots, f(x_m)) = \mathcal{N}(f|\mu(\mathbf{X}), \mathbf{\Sigma}(\mathbf{X}))\]
dove
\[\begin{split} \mu(\mathbf{X})_i &= m(x_i) \\ \mathbf{\Sigma}(\mathbf{X})_{i,j} &= \kappa(x_i, x_j) \\ \end{split}\]
3.1 Sampling from GP
Per ogni sottoinsieme \(\mathbf{X} = (x_1, \ldots, x_m)\) di \(\chi\) possiamo campionare da \(p(f)\) i valori di \(f(x_1), \ldots, f(x_m)\) andando a campionare da \(\mathcal{N}(f|\mu(\mathbf{X}), \mathbf{\Sigma}(\mathbf{X}))\) dove \(\mu\) e \(\mathbf{\Sigma}\) sono definiti come menzionato prima, ovvero
\[\begin{split} \mu(\mathbf{X})_i &= m(x_i) \\ \mathbf{\Sigma}(\mathbf{X})_{i,j} &= \kappa(x_i, x_j) \\ \end{split}\]
3.2 RBF Kernel
Tipicamente in prima istanza si assume sempre che \(m(x) = 0\) e che per rappresentare la covarianza si utilizza la RBF kernel
\[\kappa(x_1, x_2) = \sigma^2 \cdot \text{exp} \Bigg(- \frac{||x_1 - x_2||^2}{2 \tau^2} \Bigg)\]
che tende ad assegnare un valore di covarianza altro tra \(f(x_1)\) e \(f(x_2)\) se \(x_1\) e \(x_2\) sono punti vicini.
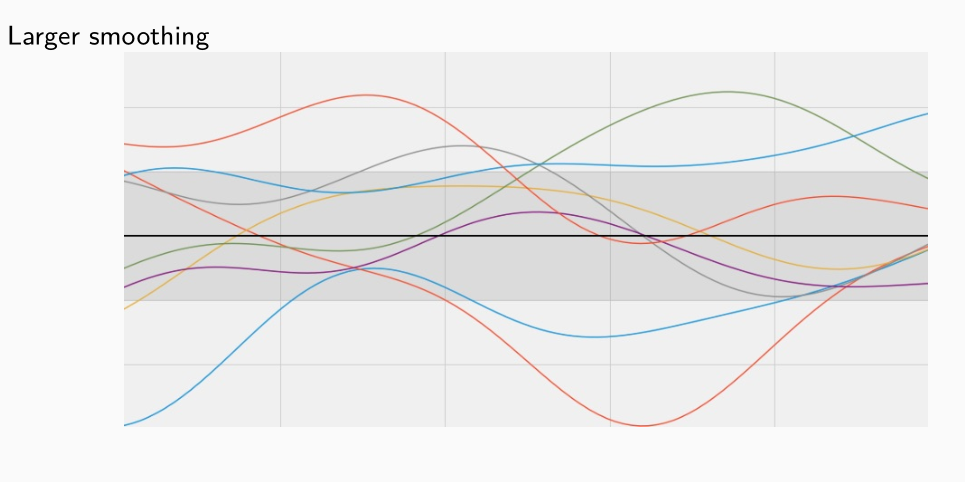
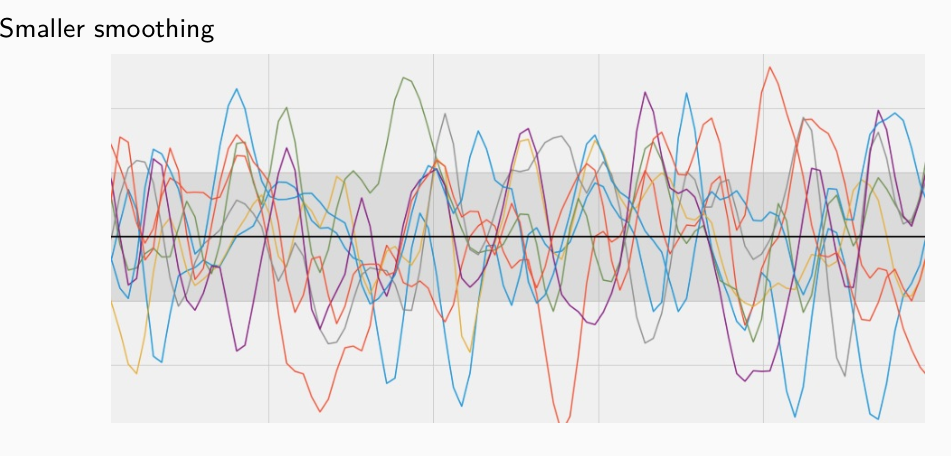
Le funzioni estratte da un processo gaussiano che utilizza una RBK kernel tendono ad essere molto smooth, ovvero elementi vicini vengono mappati dalla funzione in valori a loro volta vicini. Più alto il valore di \(\tau\) è, e più smooth la funzione risulterà.
La scala della distribuzione è determinata invece da \(\sigma^2\).
4 Gaussian Process Regression
Andiamo adesso a discutere come possiamo utilizzare un processo gaussiano per fare regressione. A tale fine assumiamo, come al solito, che il valore \(t_k\) osservato per una variabile \(x_k\) deriva da una funzione \(f(x_k)\) a cui è stato aggiunto un rumore gaussiano indipendente dal valore effettivo
\[t_k = f(x_k) + \epsilon \;\;\;,\;\;\; p(\epsilon) = \mathcal{N}(\epsilon | \mathbf{0}, \sigma^2 \mathbf{I})\]
Riassumendo quindi,
\[p(t|f,x) = \mathcal{N}(t|f(x), \sigma^2 \mathbf{I})\]
A questo punto ricordiamo che un processo gaussiano \(p(f) = \mathcal{GP}(m, \kappa)\) ci fornisce una distribuzione a priori sulle funzioni in \(\mathcal{H}\). Se poi assumiamo che i valori medi siano tutti uguali a \(0\) otteniamo che \(p(f) = \mathcal{GP}(0, \kappa)\).
Dato un insieme di osservazioni \(\mathbf{X} = \{x_i\}, \,\, \mathbf{t} = \{t_i\}\) per \(i = 1, \ldots, m\) possiamo derivare una distribuzione a posteriori delle funzioni.
È possibile dimostrare che la distribuzione a posteriori di queste funzioni è nuovamente distribuita nuovamente un processo gaussiano, con una funzione media e una funzione kernel diversa. In particolare,
\[p(f|\mathbf{X}, \mathbf{t}) = \mathcal{GP}(m_p, \kappa_p)\]
dove,
\[\begin{split} m_p(x) &= \kappa(x, \mathbf{X})(\mathbf{\Sigma}(\mathbf{X}) + \sigma^2 \mathbf{I})^{-1} \mathbf{t} \\ \kappa_p(x, x^{'}) &= \kappa(x, x^{'}) - \kappa(x, \mathbf{X})(\mathbf{\Sigma}(\mathbf{X}) + \sigma^2 \mathbf{I})^{-1} k(\mathbf{X}, x^{'}) \\ \\ k(x, \mathbf{X}) &= \Big[ \kappa(x, x_1), \ldots, \kappa(x, x_m) \Big] \\ k(\mathbf{X}, x) &= \Big[ \kappa(x_1, x), \ldots, \kappa(x_m, x) \Big] \\ \end{split}\]
L'idea è quindi quella di calcolare la distribuzione a posteriori per poi andare a campionare da essa.
Per effettuare la regressione vera e propria dobbiamo calcolare la distribuzione predittiva \(p(f|x)\) per un nuovo elemento \(x\). A tale fine notiamo che per una qualunque funzione \(f\) estratta da \(\mathcal{GP}(0, \kappa)\), la distribuzione marginale su un qualunque insieme di punti di input \(\mathbf{X} = (x_1, \ldots, x_m)\) è una multivariata gaussiana con
\[p(f(x_1), \ldots, f(x_m)) = \mathcal{N}(\mathbf{X}|\mathbf{0}, \mathbf{\Sigma}(\mathbf{X}))\]
con la solita matrice di covarianza \(\mathbf{\Sigma}(\mathbf{X})_{i,j} = \kappa(x_i, x_j)\).
Consideriamo quindi il caso in cui \(\mathbf{X}\) siano i punti del training set, e \(x\) sia il nuovo elemento rispetto al quale dobbiamo effettuare la predizione. Allora,
\[p(f(x_1), \ldots, f(x_m), f(x)) = \mathcal{N}(\mathbf{X}|\mathbf{0}, \mathbf{\Sigma}(\mathbf{X} \cup \{x\}))\]
dove,
\[\begin{split} \mathbf{\Sigma}(\mathbf{X} \cup \{x\}) = \begin{bmatrix} \mathbf{\Sigma}(\mathbf{X}) & k(\mathbf{X}, x) \\ k(x, \mathbf{X}) & \kappa(x, x) \\ \end{bmatrix} \end{split}\]
Ricoridamo però che noi non conosciamo i valori effetti \(f(x_i)\) ma conosciamo solamente \(t_i = f(x_i) + \epsilon\) con \(\epsilon\) rumore gaussiano con media \(0\) e varianza \(\sigma^2\). Prendendo in considerazione questa ulteriore informazione otteniamo
\[\begin{split} p(t_1, \ldots, t_m, t | x, \mathbf{X}; \sigma^2) &= p(\mathbf{t}, t | x, \mathbf{X}; \sigma^2) \\ &= p(f(x_1) + \epsilon, \ldots, f(x_m) + \epsilon, f(x) + \epsilon | x, \mathbf{X}; \sigma^2) \\ &= \mathcal{N}(\mathbf{0}, \mathbf{\Sigma}(\mathbf{X} \cup \{x\}) + \sigma^2 \mathbf{I}) \\ \end{split}\]
A questo punto dalle proprietà delle gaussiane multivariate a partire da quanto ottenuto possiamo trovare l'espressione per la distribuzione predittiva, ovvero
\[p(f(x) + \epsilon | f(x_1) + \epsilon, \ldots, f(x_m) + \epsilon, x, \mathbf{X}; \sigma^2)\]
In particolare, impostando
\[\begin{split} x_A &= (f(x_1) + \epsilon, \ldots, f(x_m) + \epsilon)\\ x_B &= f(x) + \epsilon \\ \end{split}\]
otteniamo
\[\begin{split} p(t | x, \mathbf{X}, \mathbf{t}) = \mathcal{N}(y | \overline{\mu}(x), \overline{\sigma^2}(x)) \end{split}\]
con,
\[\begin{split} \overline{\mu}(x) &= k(x, \mathbf{X})(\mathbf{\Sigma}(\mathbf{X}) + \sigma^2 \mathbf{I})^{-1} \mathbf{t} = \sum\limits_{i = 1}^m \alpha(x_i, x) t_i \\ \overline{\sigma}^2(x) &= \kappa(x, x) + \sigma^2 - \kappa(x, \mathbf{X})(\mathbf{\Sigma}(\mathbf{X}) + \sigma^2 \mathbf{I})^{-1}k(x, \mathbf{X})^T \\ \end{split}\]
Notiamo che il risultato finale è simile a quello ottenuto inizialmente per la regressione lineare tramite funzione kernel. In particolare la predizione è ottenuta come combinazione lineare tra i valori target del training set, ciascun pesato rispetto a quanto l'elemento associato \(x_i\) è "simile" all'elemento da predirre \(x\), dove la similarità è misurata dalla funzione kernel \(\alpha()\).
4.1 Estimating Kernel Parameters
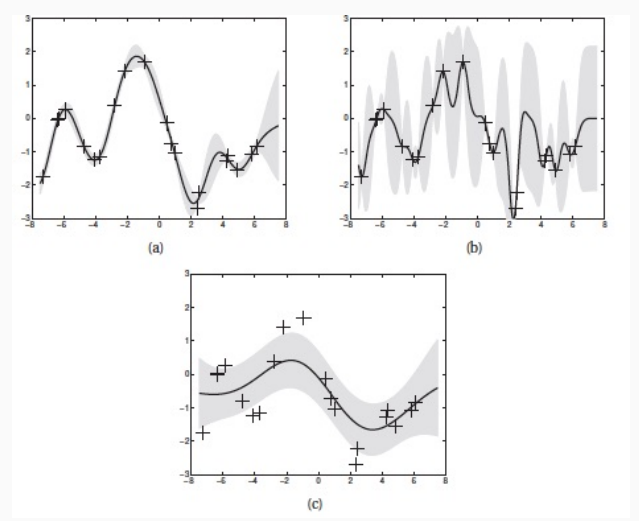
Le prestazioni predittive della regressione tramite processi gaussiani dipendono in modo significativo dalla funzione kernel scelta.
Consideriano la RBF kernel, otteniamo
\[\kappa(x_i, x_j) = \sigma^2_f e^{-\frac12 (x_i - x_j)^T M(x_i - x_j)} + \sigma^2_y \delta_{i,j}\]
all'interno di questa definizione possiamo notare diversi parametri. A seconda del valore di questi parametri otteniamo diverse prestazioni.