ML - 20 - Support Vector Machines II

Per ogni valore \(x\), questo valore è un ottimo \(x = x^*\) se e solo se esistono \(\mathbf{\lambda}^*\) e \(\mathbf{\mu}^*\) tali che

\[\begin{split} \frac{\partial L(x, \lambda, \mu)}{\partial x} &\Bigg|_{x^*, \lambda^*, \mu^*} = \mathbf{0} \\ \text{where } \\ &g_i(x^*) \leq 0 \,\,\,\,\,\,\,\, &i = 1,\ldots, k \\ &h_j(x^*) = 0 \,\,\,\,\,\,\,\,\, &j = 1,\ldots, k^{'} \\ &\lambda_i^* \geq 0 \,\,\,\,\,\,\,\, &i = 1,\ldots, k \\ &\lambda_i^* g_i(x^*) = 0 \,\,\,\,\,\,\,\, &i = 1,\ldots, k \\ \end{split}\]

dove i primi due vincoli sono conseguenza del fatto che il punto \(x^*\) deve essere un punto nella regione ammissibile del problema originario, il terzo vincolo era quello che avevamo trovato nella formulazione del problema con il lagrangiano, e l'ultimo vincolo ci dice che il moltiplicatore Lagrangiano \(\lambda_i^*\) può essere diverso da zero solamente se \(g_i(x^*) = 0\), ovvero se \(x\) si trova "al limite" rispetto al vincolo imposto su \(g_i(x)\). In questo caso diciamo che il vincolo è attivo.

Notiamo poi che per avere che il punto di ottimo è proprio un minimo, dato che ci troviamo in un contesto multivariato, dobbiamo avere che la matrice Hessiana \(H_x\) valutata sul punto \(x^*\) deve essere definita positiva.

Andiamo adesso ad applicare quanto detto per il nostro particolare problema di minimizzazione. Nel nostro particolare caso notiamo la seguente corrispondenza

• \(f(x)\) corrisponde a \(\frac12 ||\mathbf{f}w||^2\).

• \(g_i(x)\) corrisponde a \(t_i(\mathbf{w}^T \phi(x_i) + w_0) - 1 \geq 0\).

• Non c'è nessun \(h_j(x)\).

• \(\Omega\) è l'intersezione di un insieme di iperpiani, ovvero un poliedro convesso.

Mettendo tutto questo assieme otteniamo che il corrispondente Lagrangiano al problema iniziale è il seguente

\[\begin{split} L(\mathbf{w}, w_0, \mathbf{\lambda}) &= \frac12 \mathbf{w}^T \mathbf{w} - \sum\limits_{i = 1}^n \lambda_i \Big(t_i(\mathbf{w}^T \phi(x_i) + w_0) - 1 \Big) \\ &= \frac12 \mathbf{w}^T \mathbf{w} - \sum\limits_{i = 1}^n \lambda_i t_i (\mathbf{w}^T \phi(x_i) + w_0) + \sum\limits_{i = 1}^n \lambda_i \\ \end{split}\]

L'ottimo del problema originale è quindi uguale all'ottimo del seguente problema

\[\begin{split} &\underset{\mathbf{\lambda}}{\max} \,\,\, &\underset{\mathbf{w}, w_0}{\min} \,\,\, L(\mathbf{w}, w_0, \mathbf{\lambda}) \\ &\text{where } \\ & \, &\lambda_i \geq 0 \,\,\,\,\, i = 1,\ldots, k \\ \end{split}\]

Traducendo le condizioni KKT con questa particolare formulazione otteniamo che \(\mathbf{w}^*, w_0^*\) è un ottimo se e solo se esiste \(\mathbf{\lambda}^*\) tale che

\[\begin{split} \frac{\partial L(\mathbf{w}, w_0, \mathbf{\lambda})}{\partial \mathbf{w}} &\Bigg|_{\mathbf{w}^*, w_0^*, \lambda^*} = \mathbf{w}^* - \sum\limits_{i = 1}^n \lambda_i^* t_i \phi(x_i) = \mathbf{0} \\ \frac{\partial L(\mathbf{w}, w_0, \mathbf{\lambda})}{\partial w_0} &\Bigg|_{\mathbf{w}^*, w_0^*, \lambda^*} = \sum\limits_{i = 1}^n \lambda_i^* t_i = 0 \\ \\ \text{where } \\ &t_i({\mathbf{w}^*}^T \phi(x_i) + w_0^*) - 1 \geq 0 \,\,\,\,\,\,\,\, &i = 1,\ldots, n \\ &\lambda_i^* \geq 0 \,\,\,\,\,\,\,\, &i = 1,\ldots, n \\ &\lambda_i^* \Big(t_i({\mathbf{w}^*}^T \phi(x_i) + w_0^*) - 1 \Big) = 0 \,\,\,\,\,\,\,\, &i = 1,\ldots, k \\ \end{split}\]

Per la struttura della funzione obiettivo poi abbiamo che la corrispondente matrice Hessiana è la matrice identità \(H(\mathbf{w}) = \mathbf{I}\), che è sempre definita positiva, in quanto è simmetrica con autovalori positivi. Questo significa che l'ottimo è un punto di minimo, che è proprio ciò che vogliamo.

Notiamo che dalle relazioni riportate prima avevamo trovato che all'ottimo valevano le seguenti relazioni

\[\begin{cases} \mathbf{w}^* = \sum\limits_{i = 1}^n \lambda_i t_i \phi(x_i) \\ \sum\limits_{i = 1}^n \lambda_i^* t_i = 0 \\ \end{cases}\]

A questo punto siamo in grado di definire la versione duale del problema di partenza andando ad applicare le relazioni riportate prima al fine di eliminare \(\mathbf{w}\) e \(w_0\) da \(L(\mathbf{w}, w_0, \mathbf{\lambda})\) e da tutti i vincoli. Il problema ottenuto è il seguente, ed è espresso solamente in termini di \(\lambda\).

\[\begin{split} &\underset{\mathbf{\lambda}}{\max} \,\,\, & \overline{L}(\mathbf{\lambda}) = \underset{\mathbf{\lambda}}{\max} \,\,\, \Bigg(\sum\limits_{i = 1}^n \lambda_i - \frac12 \sum\limits_{i = 1}^n \sum\limits_{j = 1}^n \lambda_i \lambda_j t_i t_j \phi(x_i)^T \cdot \phi(x_j) \Bigg) \\ &\text{where } \\ & \, &\lambda_i \geq 0 \,\,\,\,\, i = 1,\ldots, n \\ & \, &\sum\limits_{i = 1}^n \lambda_i t_i = 0 \\ \end{split}\]

Questo nuovo problema avrà lo stesso valore all'ottimo del problema primale da cui siamo partiti, valore in cui le condizioni KKT saranno rispettate.

Per iniziare a risolvere il problema duale notiamo che il numero di variabili in gioco nel problema primale era \(d+1\), mentre le variabili nel problema primale sono una per ogni vincolo, e dato che abbiamo un vincolo per ognni elemento del training set, in totale abbiamo \(n\) variabili, e tipicamente \(n > d\). Questo significa che passando dal problema primale a quello duale ho aumentato la dimensionalità del problema.

Notiamo inoltre che nella funzione obiettivo da ottimizzare gli elementi del training set compaiono sempre in coppie come elementi di un prodotto scalare. L'idea è quindi quella di definire la seguente funzione kernel

\[\kappa(x_i, x_j) = \phi(x_i)^T \cdot \phi(x_j)\]

e questo ci permette di riscrivere il problema nel seguente modo

\[\begin{split} &\underset{\mathbf{\lambda}}{\max} \,\,\, & \overline{L}(\mathbf{\lambda}) = \underset{\mathbf{\lambda}}{\max} \,\,\, \Bigg(\sum\limits_{i = 1}^n \lambda_i - \frac12 \sum\limits_{i = 1}^n \sum\limits_{j = 1}^n \lambda_i \lambda_j t_i t_j \kappa(x_i, x_j) \Bigg) \\ &\text{where } \\ & \, &\lambda_i \geq 0 \,\,\,\,\, i = 1,\ldots, n \\ & \, &\sum\limits_{i = 1}^n \lambda_i t_i = 0 \\ \end{split}\]

Nel passaggio dal problema primale al problema duale quindi abbiamo aumentato il numero di variabili da \(m\) a \(n\). Inizialmente questo sembra essere un vero e proprio svantaggio. Andando a vedere le cose con più attenzione risulterà che il numero di variabili che devono essere considerate quando andiamo a classificare sarà un numero molto minore di \(n\).

Supponiamo adesso di aver risolto il problema duale, e siano \(\mathbf{\lambda}^*\) i valori ottimali dei moltiplicatori Lagrangiani. Ritornando al problema primale, i valori ottimali dei parametri \(\mathbf{w}^*\) sono ottenuti tramite la seguente relazione

\[w_i^* = \sum\limits_{j = 1}^n \lambda_j^* t_j \phi_i(x_j) \;\;\;\;\; i = 1, \ldots, m\]

mentre il valore di \(w_0^*\) può essere ottenuto in modo indiretto osservando che, per ogni vettore di supporto \(x_k\), ovvero per qualunque elemento per il quale il vincolo corrispondente è attivo, ovvero vale l'uguaglianza nel vincolo corrispondente, e quindi \(\lambda_k \geq 0\), deve valere che

\[\begin{split} 1 &= t_k \Big(\phi(x_j)^T \mathbf{w}^* + w_0^* \Big) \\ &= t_k\Bigg(\sum\limits_{j = 1}^n \lambda_j^* t_j \phi(x_j)^T \cdot \phi(x_k) + w_0^* \Bigg) \\ &= t_k\Bigg(\sum\limits_{j = 1}^n \lambda_j^* t_j \kappa(x_j, x_k) + w_0^* \Bigg) \\ &= t_k\Bigg(\sum\limits_{j \in \mathcal{S}} \lambda_j^* t_j \kappa(x_j, x_k) + w_0^* \Bigg) \\ \end{split}\]

dove \(\mathcal{S}\) è l'insieme degli indici i cui relativi vincoli sono attivi (notiamo infatti che se \(j \not \in \mathcal{S}\), allora necessariamente \(\lambda_j^* = 0\), e quindi possiamo non considerarlo).

Dato poi che \(t_k = \pm 1\), per avere un prodotto unitario, deve valere la seguente condizione

\[t_k = \sum\limits_{j \in \mathcal{S}} \lambda_j^* t_j \kappa(x_j, x_k) + w_0^*\]

che ci permette di esplicitare il valore di \(w_0^*\) nel seguente modo

\[w_0^* = t_k - \sum\limits_{j \in \mathcal{S}} \lambda_j^* t_j \kappa(x_j, x_k)\]

Una soluzione più precisa può essere ottenuta andando a calcolare il valore di emdia ottenuto considerando tutti i support vectors come segue

\[w_0^* = \frac{1}{|\mathcal{S}|} \sum\limits_{i \in \mathcal{S}} \Bigg( t_i - \sum\limits_{j \in \mathcal{S}} \lambda_j^* t_j \kappa(x_j, x_i) \Bigg)\]

Questi vincoli devono dunque essere rilassati in modo tale da permettere che non valgano ma andando ad associare un costo che cresce al crescere della violazione del vincolo originale. Si introduce quindi delle slack variable \(\xi_i\), una per vincolo, il cui obiettivo è proprio quello di misurare quanto il vincolo non è verificato.

La nuova formulazione del problema è quindi la seguente

\[\begin{split} &\underset{\mathbf{w}, \,\, w_0, \,\, \mathbf{\xi}}{\min} \,\,\, \frac12 \mathbf{w}^T \mathbf{w} + C \cdot \sum\limits_{i = 1}^n \xi_i \\ &\text{where } \\ & \, t_i(\mathbf{w}^T \phi(x_i) + w_0) \geq 1 - \xi_i & \,\,\,\,\, i = 1,\ldots, n \\ & \, \xi_i \geq 0 & \,\,\,\,\, i = 1,\ldots, n \\ \end{split}\]

dove \(\mathbf{\xi} = (\xi_1, \ldots, \xi_n)\) e l'iperparametro \(C\) determina quanto vogliamo pesare il fatto che i vincoli siano soddisfatti o insoddisfatti.

Introducendo degli opportuni moltiplicatori di Lagrange siamo in grado di ottenere il seguente Lagrangiano

\[\begin{split} L(\mathbf{w}, &w_0, \xi, \lambda, \alpha) = \\ &= \frac12 \mathbf{w}^T \mathbf{w} + C \sum\limits_{i = 1}^n \xi_i - \sum\limits_{i = 1}^n \lambda_i(y_i(\mathbf{w}^T \phi(x_i) + w_0) - 1 + \xi_i) - \sum\limits_{i = 1}^n \alpha_i \xi_i \\ &= \frac12 \sum\limits_{i = 1}^n w_i^2 + \sum\limits_{i = 1}^n (C - \alpha_i) \xi_i - \sum\limits_{i = 1}^n \lambda_i\bigg(t_i \Big(\sum\limits_{j = 1}^m w_j \phi_j(x_i)\Big) + w_0\bigg) - 1 + \xi_i \\ &= \frac12 \sum\limits_{i = 1}^n w_i^2 + \sum\limits_{i = 1}^n (C - \alpha_i - \lambda_i) \xi_i - \sum\limits_{i = 1}^n \sum\limits_{j = 1}^m \lambda_i t_i w_j \phi_j(x_i) + w_0 \sum\limits_{i = 1}^n \lambda_i t_i + \sum\limits_{i = 1}^n \lambda_i \\ \end{split}\]

Le condizioni KKT (Karush-Kuhn-Tucker) in questo caso sono le seguenti

\[\begin{split} \frac{\partial}{\partial \mathbf{w}} L(&\mathbf{w}, w_0, \xi, \lambda, \alpha) = \mathbf{0} \\ \frac{\partial}{\partial w_0} L(&\mathbf{w}, w_0, \xi, \lambda, \alpha) = 0 \\ \frac{\partial}{\partial \xi} L(&\mathbf{w}, w_0, \xi, \lambda, \alpha) = \mathbf{0} \\ \text{where } \\ &t_i(\mathbf{w}^T \phi(x_i) + w_0) - 1 + \xi_i \geq 0 \,\,\,\,\,\,\,\, &i = 1,\ldots, n \\ &\xi_i \geq 0 \,\,\,\,\,\,\,\, &i = 1,\ldots, n \\ &\lambda_i \geq 0 \,\,\,\,\,\,\,\, &i = 1,\ldots, n \\ &\alpha_i \geq 0 \,\,\,\,\,\,\,\, &i = 1,\ldots, n \\ &\lambda_i\Big(t_i(\mathbf{w}^T \phi(x_i) + w_0) - 1 + \xi_i \Big) = 0 \,\,\,\,\,\,\,\, &i = 1,\ldots, n \\ &\alpha_i \xi_i \geq 0 \,\,\,\,\,\,\,\, &i = 1,\ldots, n \\ \end{split}\]

Dalle condizioni KTT siamo in grado di derivare le seguenti relazioni

\[\begin{split} &w_i = \sum\limits_{j = 1}^n \lambda_j t_j \phi_i(x_j) \,\,\,\,\, i = 1, \ldots, m \\ &0 = \sum\limits_{i = 1}^n \lambda_i t_i \\ &\lambda_i = C - \alpha_i \leq C \,\,\,\,\, i = 1, \ldots, n \\ \end{split}\]

che ci permettono quindi derivare il seguente problema duale

\[\begin{split} &\underset{\mathbf{\lambda}}{\max} \,\,\, & \overline{L}(\mathbf{\lambda}) = \underset{\mathbf{\lambda}}{\max} \,\,\, \Bigg(\sum\limits_{i = 1}^n \lambda_i - \frac12 \sum\limits_{i = 1}^n \sum\limits_{j = 1}^n \lambda_i \lambda_j t_i t_j \phi(x_i)^T \cdot \phi(x_j) \Bigg) \\ &\text{where } \\ & \, &0 \leq \lambda_i \leq C \,\,\,\,\, i = 1,\ldots, n \\ & \, &\sum\limits_{i = 1}^n \lambda_i t_i = 0 \\ \end{split}\]

che è simile al caso con le classi separabili con l'unica differenza che il vincolo \(0 \leq \lambda_i\) si è trasformato nel nuovo vincolo \(0 \leq \lambda_i \leq C\).

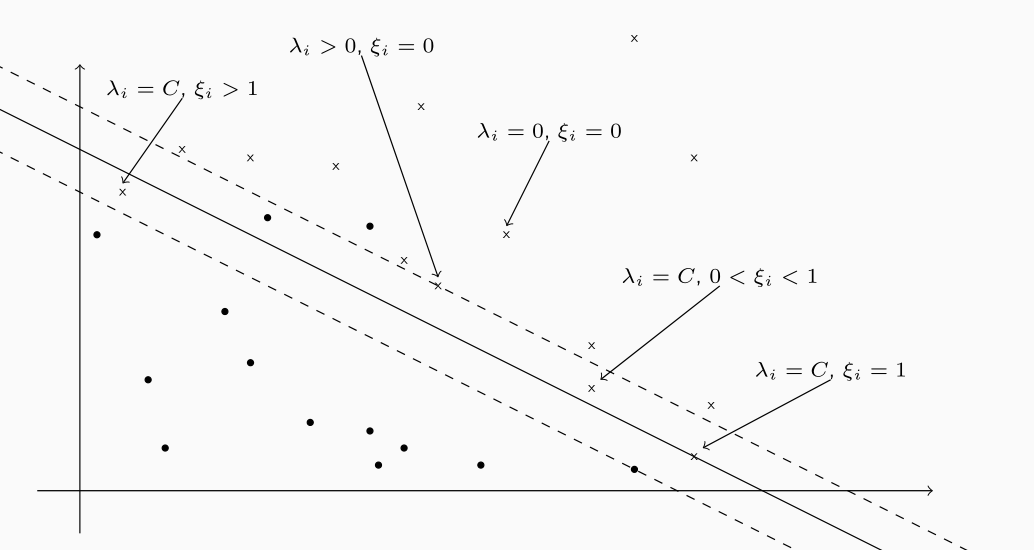
Data una soluzione al problema precedente, gli elementi del training set possono quindi essere partizionati in vari sottoinsiemi, tra cui troviamo:

• Gli elementi per cui \(\lambda_i = 0\) e \(\xi_i = 0\), ovvero gli elementi che sono correttamente classificati e che non sono rilevanti, ovvero che non si trovano sui margini.

• Gli elementi per cui \(\lambda_i > 0\) e \(0 \leq \xi_i < 1\), ovvero gli elementi che sono classificati correttamente e rilevanti, nel senso che si trovano sul margine.

• Gli elementi per cui \(\lambda_i > 0\) e \(\xi_i > 1\), ovvero gli elementi che sono classificati male.

Graficamente troviamo

A partire da una soluzione ottimale \(\lambda^*\) per il problema duale, i coefficienti \(\mathbf{w}^*\) e \(b^*\) possono essere derivati esattamente come abbiamo nel caso precedente.

In particolare un elemento \(x\) può essere classificato considernado il segno della seguente espressione

\[y(x) = \sum\limits_{i = 1}^m w_i^* \phi_i(x) + b^*\]

oppure, equivalentemente,

\[y(x) = \sum\limits_{i \in \mathcal{S}} \lambda_j^* t_j \kappa(x_i, x_j) + b^*\]

dove \(\mathcal{S}\) come al solito è l'insieme dei support vectors.