ML - 23 - Neural Networks I
Lecture Info
Date:
Lecturer: Giorgio Gambosi
Slides: (ml_11_neural-slides.pdf)
In questa lezione abbiamo introdotto il primo modello di rete neurale, i multi-layered percerptons, discutendone un caso particolare con tre layers (input, hidden, output).
1 Multilayer Networks
I modelli considerati fino a questo punto del corso sono tutti detti a single level of parameters. Questi modelli seguono infatti una struttura lineare, in generale esprimibile dalla relazione \(y = f(\mathbf{w}^T \phi(x))\), ovvero in cui i parametri del modello sono applicati direttamente ai valori di input.
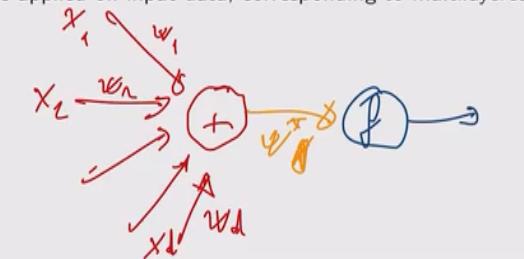
Volendo generalizzare, è possibile definire dei modelli più generali in cui sequenze di trasformazioni vengono applicate ai dati. Questi modelli sono quindi rappresentabili da mutlilayered networks of functions. Una struttura di tipo multi-layered questo tipo prende il nome di neural network (rete neurale).
2 Multi-Layered Percerpton
Un caso particolare di rete neurale è detta multi-layered perceprton.
2.1 First Layer
Per un qualsiasi vettore di input di \(d\) elementi \(x = (x_1, \ldots, x_d)\), il primo layer di una rete neurale è caratterizzato da \(m_1 > 0\) valori \(a_1^{(1)}, \ldots, a_{m_1}^{(1)}\), detti activations, che sono ottenuti combinando con gli elementi di input tramite dei pesi attraverso una combinazione lineare
\[a_{j}^{(1)} = \sum\limits_{i = 1}^d w_{ji}^{(1)} x_i + w_{j0}^{(1)} = \overline{\mathbf{x}}^T \mathbf{w}_j^{(1)}\]
dove \(w_{ji}\) è il peso dell'arco che collega la feature \(i\) al nodo \(j\) e \(\overline{\mathbf{x}} = (1, x_1, \ldots, x_d)^T\).
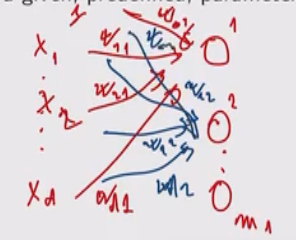
Il totale dei coefficienti nel primo layer è quindi \((d+1) \cdot m_1\), dove \(m_1\) è un iperparametro del modello.
Ogni attivazione \(a_j^{(1)}\) è trasformata utilizzando una funzione di attivazione non lineare \(h_1\) per ottenere il valore \(z_j^{(1)}\).
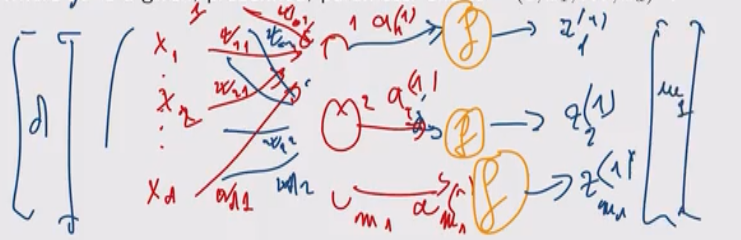
Alla fine quindi l'output del layer è un vettore \(\mathbf{z}^{(1)} = (z_1^{(1)}, \ldots, z_{m_1}^{(1)})\) con
\[z_j^{(1)} = h_1(a_j^{(1)}) = h_1\big(\overline{\mathbf{x}}^T \mathbf{w}_j^{(1)}\big)\]
Tipicamente possiamo assumere che la funzione \(h_1\) è una funzione di tipo sigmoide, ovvero
\[\sigma(x) = \frac{1}{1 + e^{-x}}\]
oppure una tangente iperbolica
\[\tanh{(x)} = \frac{e^x - e^{-x}}{e^x + e^{-x}} = \frac{1}{1 + e^{-2x}} - \frac{1}{1 + e^{ex}} = \sigma(2x) - \sigma(-2x)\]
2.2 Second Layer
Continuando la nostra costruzione, possiamo utilizzare il vettore \(\mathbf{z}^{(1)}\) come input per il prossimo layer, in cui \(m_2\) hidden units sono utilizzate per calcolare un nuovo vettore \(\mathbf{z}^{(2)} = (z_1^{(2)}, \ldots, z_{m_2}^{(2)})\) andando prima a calcolare una combinazione lineare dei valori di inpu
\[a_k^{(2)} = \sum\limits_{i = 1}^{m_1} w_{ki}^{(2)} z_i^{(1)} + w_{k0}^{(2)} = (\overline{\mathbf{z}}^{(1)})^T \overline{\mathbf{w}}_k^{(2)}\]
e poi applicando una funzione non lineare \(h_2\)
\[z_k^{(2)} = h_2((\overline{\mathbf{z}}^{(1)})^T \overline{\mathbf{w}}_k^{(2)})\]
Graficamente,

Con l'introduzione di questo layer i coefficienti del modello sono divetanti \((d + 1)m_1 + (m_1 + 1)m_2\).
2.3 Inner Layers
La stessa costruzione di prima può essere iterata per ogni layer interno, dove il layer \(r\) ha \(m_r\) unità che utilizzando il vettore di input \(\mathbf{z}^{(r-1)}\) per ottenere il vettore di output \(\mathbf{z}^{(r-1)}\) tramite prima una combinazione lineare
\[a_k^{(r)} = (\overline{\mathbf{z}}^{(r-1)})^T \overline{\mathbf{w}}_k^{(r)}\]
e poi una trasformazione non lineare
\[z_k^{(r)} = h_r(a_k^{(r)}) = h_r((\overline{\mathbf{z}}^{(r-1)})^T \overline{\mathbf{w}}_k^{(r)})\]
Alla fine di tutti questi inner layers c'è poi un solo output layer.
2.4 Output Layer
Il layer di output è caratterizzato dal fatto che i valori in uscita da questo layer devono poter essere interpretati in funzione del problema che vogliamo risolvere attraverso la rete neturale.
Possibili differenze della struttura del layer di output a seconda del contesto di utilizzo:
Regressione: In questo caso l'ultimo layer ci deve fornire un valore, e quindi è costituito da un solo nodo.
Classificazione binaria: In questo caso l'ultimo layer avrà un solo elemento che ci darà il valore di probaiblità di appartenenza ad una classe.
Classicazione multiclasse: In questo caso, l'output layer dovrà avere un insieme di \(k\) valori, ciascuno dei quali rappresenta la probabilità di appartenenta dell'elemento alla particolare classe \(C_k\). In questo caso dobbiamo imporre che la somma di tali valori sia proprio \(1\).
In generale quindi il layer \(t\) (quello di output) fornisce un vettore di output \(\mathbf{y} = \mathbf{z}^{(t)}\) prodotto nuovamente da \(m_t\) output units (unità di output) che prima si occupa di calcolare una combinazione lineare
\[a_k^{(t)} = (\overline{\mathbf{z}}^{(t-1)})^T \overline{\mathbf{w}}_k^{(t)}\]
e poi applicano a quanto ottenuto una trasforamzione non lineare \(h_t\)
\[y_k = z_k^{(t)} = h_t((\overline{\mathbf{z}}^{(t-1)})^T \overline{\mathbf{w}}_k^{(t)})\]
dove la funzione \(h_t\) dipende dal particolare problema che si vuole risolvere. In particolare troviamo:
Regressione: \(h_t\) è la funzione identità.
Classificazione binaria: \(h_t\) è funzione sigmoide.
Classicazione multiclasse: \(h_t\) è la funzione softmax.
3 3-Layer Networks
Un modello abbastanza potente è un multi-layered percerpton a 3 livelli, in cui il primo livello sono i valori di input, il secondo livello è il valore della prima combinazione lineare delle features, e il terzo livello è layer di output.
Consideriamo il problema di classificare \(K\) classi diverse e utilizziamo un modello a 3 livelli. Esplicitando quello che succede nei vari layer, e assumendo che il numero di elementi nell'hidden layer sono \(M\), troviamo la seguente relazione
\[y_k = \sigma\Bigg(\sum\limits_{j = 1}^M w_{kj}^{(2)} h\Big(\sum\limits_{i = 1}^d w_{ji}^{(1)}x_i + w_{j0}^{(1)} \Big) + w_{k0}^{(2)} \Bigg)\]
La rete risultante può dunque essere vista come un caso particolare di un GLM (Generalized Linear Model), che in questo caso è una logistic regression, dove però le funzioni base non sono definite preventivamente rispetto ai dati \(x_i\) ma sono invece parametrizzate rispetto i coefficienti in \(\mathbf{w}^{(1)}\).
L'idea quindi è che in un GLM, la trasformazione delle features tramite le funzioni base è definita preventivamente e arbitrariamente. In questo caso la trasformazione delle features non è del tutto arbitaria, nel senso che la sua struttura è fissata, ma per poter essere calcolata dobbiamo fissare i valori dei coefficienti. In altre parole, non stiamo definendo come è fatta esattamente la trasformazione, ma stiamo definendo uno schema di possibili trasformazioni, che è parametrico rispetto ai coefficienti del primo layer, che sono ottenuti durante il training set, e quindi sono ottenuti in un approccio data-oriented.
Questo modello neurale quindi, a differenza di un GLM, la trasformazione delle features è un qualcosa che cambia rispetto ai dati del training set, e quindi essa stessa è appresa dal modello. Un modello di questo tipo quindi fa la miglior possibile regressione logistica utilizzando la miglior possibile trasformazione per rappresentare i dati iniziali.
Lo schema finale è quindi il seguente