ML - 24 - Neural Networks II

Supponiamo di voler effettuare regressione con una rete neurale.

In questo caso il modello probabilistico è il seguente: dato un qualunque elemento del training set \((x_i, t_i)\), il valore \(y_i = y(x_i, \mathbf{w})\) è distribuito come un gaussiana intorno al valore target \(t_i\) con una varianza \(\sigma^2\) da determinare.

Equivalentemente possiamo dire che, dato un elemento \(x\), il valore target \(t\) è sconosciuto ed è distribuito normalmente intorno al valore predetto \(y = y(x, \mathbf{w})\) con varianza \(\sigma^2\). In formula,

\[p(t|x, \mathbf{w}, \sigma^2) = \mathcal{N}(t|y(x, \mathbf{w}), \sigma^2)\]

A questo punto osserviamo che assumendo l'indipendenza del training set otteniamo che la likelihood è data da

\[L(\mathbf{t}|\mathbf{X}, \mathbf{w}, \sigma^2) = \prod\limits_{i = 1}^n p(t_i|x_i, \mathbf{w}, \sigma^2) = \prod\limits_{i = 1}^n \mathcal{N}(t_i | y(x_i, \mathbf{w}), \sigma^2)\]

e quindi la log-likelihood è data da

\[\begin{split} l(\mathbf{t}|\mathbf{X}, x, \sigma^2) &= \log{L(\mathbf{t}|x, \mathbf{w}, \sigma^2)} \\ &= -\frac{n}{2} \log{(2 \pi \sigma^2)} - \frac{1}{2 \sigma^2} \sum\limits_{i = 1}^n \Big(y(x_i, \mathbf{w}) - t_i \Big)^2 \\ \end{split}\]

Ricordando poi che massimizzare la log-likelihood rispetto a \(\mathbf{w}\) equivale a minimizzare la seguente loss function otteniamo

\[E(\mathbf{w}) = \frac12 \sum\limits_{i = 1}^n \Big(y(x_i, \mathbf{w}) - t_i\Big)^2\]

---

Andiamo adesso ad esprimere la derivata della funzione di costo rispetto ad \(a^{(2)}\), che è proprio il valore finale ritornato dalla rete neurale, in quanto stiamo trattando un problema di regressione

Otteniamo quindi

\[\begin{split} \frac{\partial E(\mathbf{w})}{\partial a^{(2)}} &= \frac12 \sum\limits_{i = 1}^n \frac{\partial}{\partial a^{(2)}} \Big(y(x_i, \mathbf{w}) - t_i \Big)^2 \\ &= \sum\limits_{i = 1}^n \Big(y(x_i, \mathbf{w}) - t_i) \Big) \cdot \frac{\partial}{\partial a^{(2)}} \Big(y(x_i, \mathbf{w}) - t_i\Big) \\ \end{split}\]

per costruzione poi abbiamo che \(y = a^{(2)}\), in quanto nel caso della regressione la funzione finale che viene applicata al valore ottenuto dalla combinazione lineare \(a^{(2)}\) è la funzione identità. Dunque otteniamo

\[\frac{\partial}{\partial a^{(2)}} (y - t) = \frac{\partial}{\partial a^{(2)}}(a^{(2)} - t) = 1\]

e quindi

\[\frac{\partial E(\mathbf{w})}{\partial a^{(2)}} = \sum\limits_{i = 1}^n \Big(y(x_i, \mathbf{w}) - t_i \Big)\]

Da questo concludiamo che ogni elemento \((x, t)\) considerato contribuisce al gradiente con il suo errore \(y(x, \mathbf{w}) - t\).

Osservazione: A differenza del caso della regressione lineare, nelle reti neurali la funzione \(y(x, \mathbf{w})\) non è lineare né convessa (in generale), e quindi può avere più minimi locali.

Nel caso della classificazione binaria invece il modello probaiblistico di riferimento è un modello in cui la probabilità condizionata del valore target, dato il valore delle features, è distribuita come una Bernoulli

\[p(t|x) = p(C_1|x)^t p(C_0|x)^{1-t}\]

Se poi assumiamo che abbiamo un modello logistico che ci permette di stimare \(p(C_1|x;\mathbf{w})\) tramite il valore \(y(x, \mathbf{w})\) otteniamo

\[p(t|x, \mathbf{w}) = y(x, \mathbf{w})^t (1 - y(x, \mathbf{w}))^{1-t}\]

La likelihood è quindi data da

\[L(\mathbf{t} | \mathbf{X}, \mathbf{w}) = \prod\limits_{i = 1}^n y(x_i, \mathbf{w})^{t_i}(1 - y(x_i, \mathbf{w}))^{1-t_i}\]

mentre la log-likelihood è data

\[l(\mathbf{t}|\mathbf{X}, \mathbf{w}) = \sum\limits_{i = 1}^n \Big(t_i \ln{y(x_i, \mathbf{w})} + (1 - t_i)\ln{(1 - y(x_i, \mathbf{w}))}\Big)\]

Continuando, la loss function è data dalla cross-entropy, definita come segue

\[E(\mathbf{w}) = - l(\mathbf{t}|\mathbf{X}, \mathbf{w}) = -\sum\limits_{i = 1}^n (t_i \ln{y_i} + (1 - t_i)\ln{(1 - y_i)})\]

dove con \(y_i\) intendiamo ovviamente \(y(x_i, \mathbf{w})\).

---

Dato che anche in questo caso nell'ultimo layer della mia rete neurale ho un solo elemento, \(a^{(2)}\), l'idea è quelal di procedere in modo analogo a quanto visto prima, andandoci a calcolare la derivata della funzione di costo rispetto ad \(a^{(2)}\).

\[\frac{\partial E(\mathbf{w})}{\partial a^{(2)}} = -\sum\limits_{i = 1}^n \Big(t_i \frac{1}{y_i} \frac{\partial y_i}{\partial a^{(2)}} - (1 - t_i) \frac{1}{1 - y_i} \frac{\partial y_i}{\partial a^{(2)}}\Big)\]

In questo caso abbiamo che per costruzione \(y = \sigma(a^{(2)}\), e quindi otteniamo

\[\frac{\partial y}{\partial a^{(2)}} = \frac{\partial \sigma(a^{(2)})}{\partial a^{(2)}} = \sigma(a^{(2)})(1 - \sigma(a^{(2)})) = y(1 - y)\]

Mettendo tutto assieme ottengo che anche in questo caso la derivata della loss function rispetto ad \(a^{(2)}\) è la somma degli errori di ciascun elemento considerato. In formula,

\[\frac{\partial E(\mathbf{w})}{\partial a^{(2)}} = \sum\limits_{i = 1}^n (y_i - t_i)\]

Nel caso di una classificazione con \(K\) classi diverse, la likelihood è definita in termini della distribuzione categorica. In formula,

\[P(\mathbf{T} | \mathbf{X}) = \prod\limits_{i = 1}^n \prod\limits_{k = 1}^K p(C_k|x_i)^{t_{i,k}}\]

dove \(\mathbf{T}\) è una matrice \(n \times K\) in cui la \(i\) esima riga è la codifica 1-to-K di \(t_i\).

Assumendo poi di utilizzare un modello softmax in cui il valore prodotto \(y_k(x, \mathbf{W})\) sia una stima del valore di probabilità \(p(C_k|x)\), otteniamo la seguente espressione

\[P(\mathbf{T} | \mathbf{X}) = \prod\limits_{i = 1}^n \prod\limits_{k = 1}^K y_k(x_i, \mathbf{W})^{t_{i,k}}\]

dove \(\mathbf{W} = (\mathbf{w}_1, \ldots, \mathbf{w}_K)\) è una matrice di dimensione \((d+1) \times K\) che contiene tutti i coefficienti del modello, e in particolare in cui \(\mathbf{w}_j\) è il vettore \(d+1\) dimensionale che contiene i coefficienti relativi alla classe \(C_j\).

La log-lileihood invece è data da

\[l(\mathbf{T}|\mathbf{X}, \mathbf{W}) = \sum\limits_{i = 1}^n \sum\limits_{k = 1}^K t_{i,k} \log{y_k(x_i, \mathbf{W}}\]

e la funzione da minimizzare, la loss function, e nuovamente

\[E(\mathbf{W}) = -l(\mathbf{T}|\mathbf{X}, \mathbf{W})\]

---

A questo punto analizziamo il valore \(y_j\) prodotto dalla rete neurale per stimare la probabilità di appartenenza alla \(j\) esima classe.

\[y_j = \frac{e^{a_j^{(2)}}}{\sum\limits_{r = 1}^K e^{a_r^{(2)}}}\]

Facendo la derivata rispetto ad \(a_j^{(2)}\) ottengo

\[\begin{split} \frac{\partial E(\mathbf{W})}{\partial a_j^{(2)}} &= -\sum\limits_{i = 1}^n \sum\limits_{k = 1}^K t_{i,k} \cdot \frac{\partial}{\partial a_j^{(2)}} \cdot \log{y_k(x_i, \mathbf{W})} \\ &= -\sum\limits_{i = 1}^n \sum\limits_{k = 1}^K t_{i,k} \cdot \frac{1}{y_k(x_i, \mathbf{W})} \cdot \frac{\partial}{\partial a_j^{(2)}} y_k(x_i, \mathbf{W}) \\ \end{split}\]

se poi consideriamo la derivata di \(y_k(x, \mathbf{W})\) rispetto a \(a_j^{(2)}\) otteniamo

\[\frac{\partial}{\partial a_j^{(2)}}y_k(x, \mathbf{W}) = \begin{cases} y_j(x, \mathbf{W})(1 - y_j(x, \mathbf{W})) &\,\,\,,\,\,\, k = j \\ -y_k(x, \mathbf{W}) \cdot y_j(x, \mathbf{W} &\,\,\,,\,\,\, k \neq j \\ \end{cases}\]

sostituendo all'espressione di prima otteniamo

\[\begin{split} \frac{\partial E(\mathbf{W})}{\partial a_j^{(2)}} &= -\sum\limits_{i = 1}^n \Bigg(t_{i,j} \cdot (1 - y_j(x_i, \mathbf{W})) - \sum\limits_{k \neq j} t_{i,k} \cdot y_j(x_i, \mathbf{W})\Bigg) \\ &= -\sum\limits_{i = 1}^n \Bigg(t_{i,j} - \sum\limits_{k = 1}^K t_{i,k} \cdot y_j(x_i, \mathbf{W}) \Bigg) \\ &= -\sum\limits_{i = 1}^n \Bigg(t_{i,j} - y_j(x_i, \mathbf{W}) \sum\limits_{k = 1}^K t_{i, k}\Bigg) \\ &= \sum\limits_{i = 1}^n (y_i(x_i, \mathbf{W}) - t_{i,k}) \\ \end{split}\]

Nuovamente, troviamo che alla fine il contributo di ogni elemento \((x, t)\) considerato contribuisce al valore della derivata rispetto all'errore per quel particolare elemento.

Un tipico metodo iterativo è la discesa del gradiente

\[\mathbf{w}^{(k+1)} = \mathbf{w}^{(k)} + \Delta \mathbf{w}^{(k)}\]

che per ogni passo esegue i seguenti due sotto-passi:

1. Come prima cosa le derivate delle funzioni di errori rispetto a tutti i pesi sono valutate nel punto analizzato.

2. I pesi sono modificati utilizzando le nuove derivate. Questo porta quindi a raggiungere un nuovo punto da analizzare.

Dato che la funzione di costo è definita come somma dei costi di ogni singolo elemento

\[E(\mathbf{w}) = \sum\limits_{i = 1}^n E_i(\mathbf{w})\]

la regola di update può essere modificata andando a considerare un solo elemento del training set alla volta

\[\mathbf{w}^{k+1} = \mathbf{w}^{(k)} - \eta \cdot \frac{\partial E_i(\mathbf{w})}{\partial \mathbf{w}} \Bigg|_{\mathbf{w}^{(k)}}\]

In questo caso il gradiente è calcolato andando a calcolare un sottoinsieme (detto batch) \(B\) del training set.

\[\mathbf{w}^{(k+1)} = \mathbf{w}^{(k)} - \eta \sum\limits_{x_i \in B} \frac{\partial E_i(\mathbf{w})}{\partial \mathbf{w}} \Bigg|_{\mathbf{w}^{(k)}}\]

La tecnica della backpropagation viene utilizzata per calcolare le derivate dell'errore rispetto a tutti i pesi e rappresenta quindi l'algoritmo utilizzato per la prima delle due fasi tipiche di un metodo iterativo "gradient discent".

Questo algoritmo è chiamato "backpropagation" in quanto può essere interpretato come una propagazione al contrario (backward propagation) di una computazione nella rete, che parte dall'output layer e và verso le unità di inputs. Fissato lo stato della rete infatti e dato un valore di \(x_i\), la rete permette di effettuare una computazione in "avanti", ovvero da sinistra verso destra, per ottenere alla fine un valore di output, che globalmente denotiamo con \(y_i\).

A questo punto, dall'osservazione della differenza \(y_i - t_i\), è possibile stimare i valori delle derivate delle funzioni di errore rispetto a tutti i coefficenti muovendosi all'indietro, ovvero da destra a sinistra.

Per ogni coefficiente (ovvero per ogni arco della rete), la back propagation fornisce il valore della derivata della funzione di errore che sto considerando rispetto al coefficiente calcolata nel punto definito dai valori attuali di tutti i coefficienti.

---

Consideriamo un punto generico di una rete neurale con una topologia arbitraria in cui le funzioni di attivazione e la funzione di errore sono tutte funzioni differenziabili.

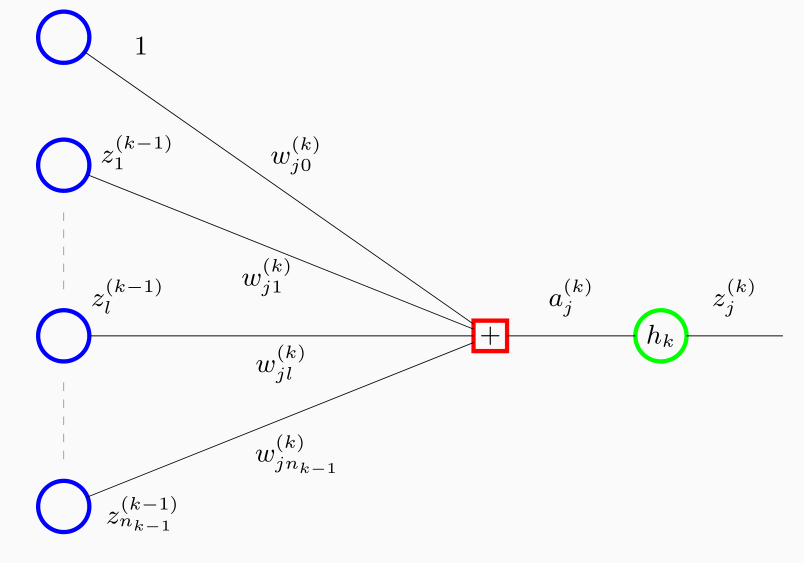
Notiamo che tutte le variabili \(z_i\) potrebbero essere sia variabili di input e sia variabili di output del layer precedente. La funzione \(h_k\) inoltre potrebbe essere la funzione identità, in modo tale che il valore finale ritornato dal layer è proprio \(a_k\).

Consideriamo adesso una funzione di errore esprimibile come somma di errori sui singoli elementi

\[E(\mathbf{w}) = \sum\limits_{i = 1}^n E_i(\mathbf{w})\]

Notiamo che se \(E_i\) è differenziabile, allora lo è anche \(E\), in quanto la sua derivata è la somma delle derivate delle funzioni \(E_i\).

Consideriamo adesso un singolo elemento del training set \((x_i, t_i)\), e mandiamo in input alla rete i valori delle features di \(x_i\). Questo step prende il nome di forward propagation.

Noi in particolare siamo interessati a calcolare il valore della derivata \(E_i\) rispetto al parametro \(w_{jl}^{(k)}\), ovvero il coefficiente che pesa il valore \(z_l^{(k-1)}\) nella combinazione lineare il cui risultato finale è \(a_j^{(k)}\). Notiamo che \(E_i\) è una funzione di \(w_{l,j}^{(k)}\) in quanto

\[a_k^{(k)} = \sum\limits_{r = 1}^m w_{j,r}^{(k)} z_{r}^{(k-1)}\]

Definendo \(\delta_j^{(k)}\) come

\[\delta_j^{(k)} = \frac{\partial E_i}{\partial a_j^{(k)}}\]

e notando che

\[\frac{\partial a_j^{(k)}}{\partial w_{j,l}^{(k)}} = \frac{\partial}{\partial w_{j,l}^{(k)}} \sum\limits_{r = 1}^m w_{j,r}^{(k)} z_r^{(k-1)} = z_l^{(k-1)}\]

otteniamo

\[\frac{\partial E_i}{\partial w_{j,l}^{(k)}} = \frac{\partial E_i}{a_j^{(k)}} \cdot \frac{\partial a_j^{(k)}}{\partial w_{j,l}^{(k)}} = \delta_j^{(k)} \cdot z_l^{(k-1)}\]

Notiamo a questo punto che noi conosciamo già il valore di \(z_l^{(k-1)}\), in quanto è stato ottenuto durante la forward propagation. L'unica cosa che necessitiamo è quindi quello di calcolare il valore \(\delta_j^{(k)}\) per ogni unità del network.

---

Osserivamo adesso che se \(z_j^{(k)} = y_j\), ovvero se il layer analizzato è l'ultimo layer, allora per quanto visto prima otteniamo

\[\delta_j^{(k)} = \frac{\partial E_i}{\partial a_j^{(k)}} = y_j - t_j\]

Consideriano invece una qualunque unità internal (hidden unit), abbiamo che una variazione del valore di \(a_j^{(k)}\) ha un influenza sul costo \(E_i\) andando ad indurre un cambio dei valori per tutte le variabili \(a_l^{(k+1)}\). L'effetto in particolare è esprimibile come la seguente funzione

\[\begin{split} \delta_j^{(k)} = \frac{\partial E_i}{\partial a_j^{(k)}} &= \sum\limits_{r = 1}^{n_k + 1} \frac{\partial E_i}{\partial a_r^{(k+1)}} \cdot \frac{\partial a_r^{(k+1)}}{\partial a_j^{(k)}} \\ &= \sum\limits_{r = 1}^{n_k + 1} \delta_r^{(k+1)} \cdot \frac{\partial a_r^{(k+1)}}{\partial a_j^{(k)}} \\ \end{split}\]

notiamo come questa relazione ci permette di esprimere una delta del layer \(k\) in funzione di tutte le delta al layer \(k+1\). Dato poi che definizione

\[\begin{split} a_r^{(k+1)} &= \sum\limits_l w_{r,l}^{(k+1)} z_l^{(k)} \\ \\ z_j^{(k)} &= h_k(a_j^{(k)}) \\ \end{split}\]

otteniamo

\[\frac{\partial a_r^{(k+1)}}{\partial a_j^{(k)}} = \frac{\partial a_r^{(k+1)}}{\partial z_j^{(k)}} \cdot \frac{\partial z_j^{(k)}}{\partial a_j^{(k)}} = w_{r,j}^{(k+1)} h^{'}_k(a_j^{(k)})\]

mettendo tutto insieme otteniamo quindi

\[\delta_j^{(k)} = h^{'}_k(a_j^{(k)}) \cdot \sum\limits_{r = 1}^{n_k + 1}\delta_r^{(k+1)} w_{r,j}^{(k+1)}\]

dato che conosco \(h_k\) conosco anche la sua derivata \(h_k^{'}\), e quindi posso facilmente calcolare il valore \(h_k^{'}(a_j^{(k)}\). Inoltre consoco anche i vari valori \(w_{r,j}^{(k+1)}\) in quanto sono i pesi nella configurazione attuale della rete. L'unico valore che potenzialmente potrei non conoscere sono i \(\delta_r^{(k+1)}\).

Osserviamo che la relazione appena ottenuta mi permette di calcolare i delta del layer \(k\) se conosco i delta del layer \(k+1\). Dato che i valori delta del layer finale li conosco, applicando in modo iterativo per ogni layer questa formula sono in grado di calcolare i valori delta di tutti i layers.

---