ML - 25 - Deep Learning I
Lecture Info
Date:
Lecturer: Giorgio Gambosi
Slides: (ml_12_deep-slides.pdf)
In questa lezione introduciamo il deep learning, andando a discutere varie tipologie di deep learning e menzionando alcune problematiche che possono insorgere durante l'allenamento di queste reti.
1 Deep Networks
Il termine deep nel contesto del machine learning e delle reti neurali tipicamente viene utilizzato per far riferimento a reti neurali che includono almeno 2 hidden layers (fino a qualche decina).
La complessità di questi modelli (ovvero il numero di coefficienti da imparare) dipende da alcuni fattori, tra cui:
Depth, ovvero il numero di layers.
Width, ovvero il numero di unità per layer.
Link topology.
Sharing di valori di coefficienti tra i links.
Più il modello è complesso e più il processo di training è costoso, sia in termine di risorse computazionali e sia in termine di size del training set.
1.1 Types
Ci sono molti tipi di deep networks. Tra queste troviamo anche i seguenti:
MLP, Multilayer percerpton.
CNN, Convolutional neural network, tipicamente utilizzate nell'elaborazione delle immagini.
AE, Auto encoder, che implementano dei metodi di compressione sofisticati.
RNN, Recurrent neural network, utilizzate quando si ha a che fare con sequenze di valori.
LSTM, Long-short term memory network, variante particolare di una RNN.
In generale molti reti neurali vengono definire in modo ad-hoc a seconda del problema che si sta affrontando andando a comporre tra loro reti neurali più semplici.
1.2 Learning
L'approccio utilizzato per il learning delle deep networks non è differente da quanto visto fino a questo punto. Si procede infatti prima definendo una loss function, e poi applicando qualche metodo di ottimizzazione, che tipicamente una versione della discesa del gradiente, per trovare il modello che minimizza la loss function.
Un elemento importante nelle reti deep è la scelta della activation function nei layer interni.
1.3 Loss Functions
Per quanto riguarda le funzioni di costo, troviamo le seguenti, a seconda del tipo di problema:
Binary classification:
Hinge
\[L = \max{(0, \,\, 1 - yt)}\]
Squared hinge
\[L = \max{(0, \,\, 1 - yt)}^2\]
Cross entropy
\[L = - (t \log{y} + (1 - t)\log{(1 - y)})\]
K-Class Classification
Hinge
\[L = \sum\limits_{j \neq t}\max{(0, \,\, 1 - (y_t - y_j))}\]
Squared hinge
\[L = \sum\limits_{j \neq t} \max{(0, \,\, 1 - (y_t - y_j))}^2\]
Cross entropy
\[L = -\sum\limits_{k = 1}^K t_k \log{y_k} = -\log{y_t}\]
Regression
L2 norm
\[L = (y -t )^2\]
L1 norm
\[L = |y - t|\]
Pseudo Huber
\[L = \delta^2 \Big(\sqrt{1 + (\frac{y-t}{\delta})^2} - 1 \Big)\]
1.4 Regularization
Dato che modelli complessi sono molto vulnerabili all'overfitting ci sono vari modi per prevenire problematiche del genere, tra cui:
L2 regularization.
L1 regularization.
Max norm constraints: si forza (clamping) un upper bound assoluto alla magnitudine dei pesi andando a forzare il vincolo \(||w|| < c\).
Dropout: Con probabilità \(p\) si mantiene attivo un neurone e lo si imposta a \(0\) con probabilità \(1-p\).
1.5 Vanishing Gradient
Un problema che si presenta abbastanza frequentemente nelle reti profonde è il problema del vanishing gradient.
Questo problema consiste nel fatto che durante la backpropagation, il valore del gradiente, ovvero il valore della derivata del costo rispetto ad ognuno dei coefficienti associati agli archi nella rete neurale, è determinato a partire dagli ultimi strati andando indietro verso i primi. Per effetto della struttura di attivazione in gioco, può essere che il valore in termine assoluto dei gradienti tende a diminuire man mano che si torna indietro verso i primi layer della rete. Questo porta la rete a non cambiare di tanto i valori dei primi coefficienti durante la fase di training.
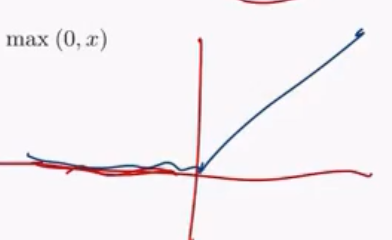
Per evitare questo problema l'idea è quella di utilizzare una funzione di attivazione diversa. Tipicamente viene utilizzata una funzione di attivazione non lineare nota con il nome di RELU (Rectified Liner Unit), definita come segue
\[h(x) = \max{(0, x)}\]
graficamente,
1.6 Exploding Gradient
Il problema opposto al vanishing gradient è detto exploding gradient, e consiste nell'avere un gradiente che cresce in modo indefinito durante la backpropagation.
Tipicamente si gestisce questo problema effettuando clipping o tramite della regolarizzazione.