ML - 26 - Deep Learning II
Lecture Info
Date:
Lecturer: Giorgio Gambosi
Slides: (ml_12_deep-slides.pdf)
In questa lezione abbiamo trattato delle convolutional neural networks, introducendo la convolution operation e discutendo della struttura dei vari layers tipicamente utilizzati in queste reti.
1 Convolutional Neural Networks
Le reti convoluzionali sono percettroni multilayer in cui però si limita la topologia delle connessioni tra due layer successivi, andando quindi a togliere la possibilità di avere connessioni dense. Ogni neurone in queste reti riceve un input, esegue un prodotto scalare e eventualmente applica una funzione non-lineare.
Nei nostri esempi l'input da dare in pasto a queste reti sono sempre immagini, rappresentate da pixels, e il compito della rete è quello di classificare l'immagine in modo appropriato.
L'ultimo layer di queste reti è un layer tradizionale completamente connesso con una certa funzione di loss, che dipende dal particolare modello.
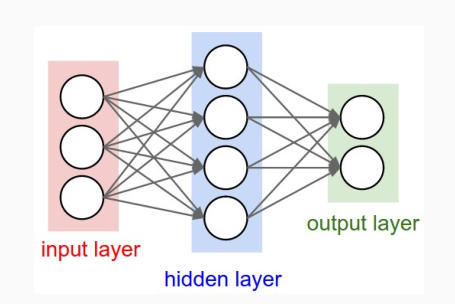
1.1 MLP Problems with Images
Ricordiamo che la struttura base di un MLP è la seguente
E consideriamo il dataset CIFAR-10, che contiene delle immagini di size \(32 \times 32 \times 3\).

Questo significa che una immagine in input è rappresentata da \(32 \cdot 32 \cdot 3 = 3072\) valori. Ciascun neurone al primo layer dovrà quindi avere \(3073\) archi entranti.
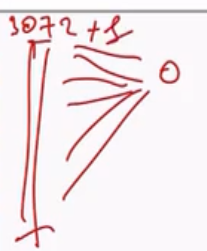
Andando ad aumentare ancora di più la risoluzione delle immagini avremmo che ciascun neurone del primo layer avrebbe ancora più archi entranti. Notiamo come questo fa crescere in modo spropositato il numero di coefficienti in gioco.
1.2 Convolution Operation
Per gestire questo problema di esplosione di coefficienti, tipicamente alle immagini viene applicata una operazione che prende il nome di convolution (convoluzione).
Questa operazione fa utilizzo di un appropriato filtro, detto kernel, rappresentato da una matrice di coefficienti, e consiste nel raggruppare più valori dell'immagine in un singolo valore.
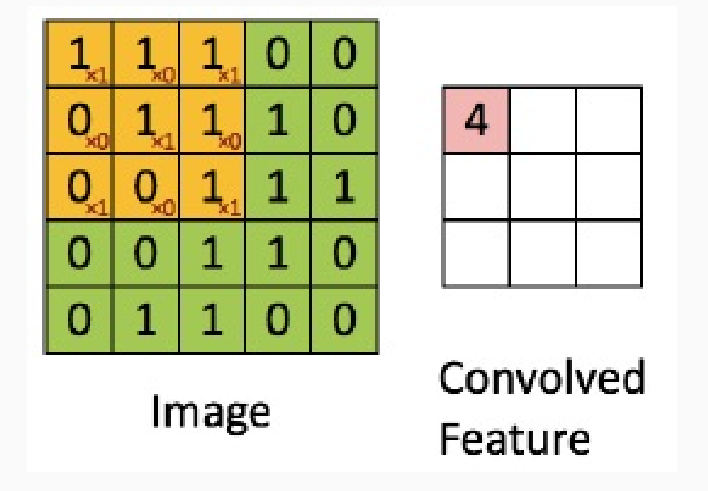
Il valore ottenuto è dato dalla somma dei valori della matrice moltiplicati per i valori del filtro. In questo caso troviamo
\[1 \cdot 1 + 0 \cdot 1 + 1 \cdot 1 + 0 \cdot 0 + 1 \cdot 1 + 0 \cdot 1 + 1 \cdot 0 + 0 \cdot 0 + 1 \cdot 1 = 4\]
Per ogni possibile posizione del filtro rispetto la matrice di partenza siamo in grado di ottenere una matrice \(3 \times 3\). Così facendo quindi abbiamo riportato una matrice \(5 \times 5\) in una \(3 \times 3\).
L'idea delle convolutional neural networks è proprio quella di applicare questo tipo di operazione per passare da un layer con \(25\) neuroni ad uno con \(5\) neuroni. A differenza del MLP poi, il valore assunto dal neurone di output non viene calcolato in funzione dei valori di tutti i neuroni di input, ma solo da un sottoinsieme di questi.
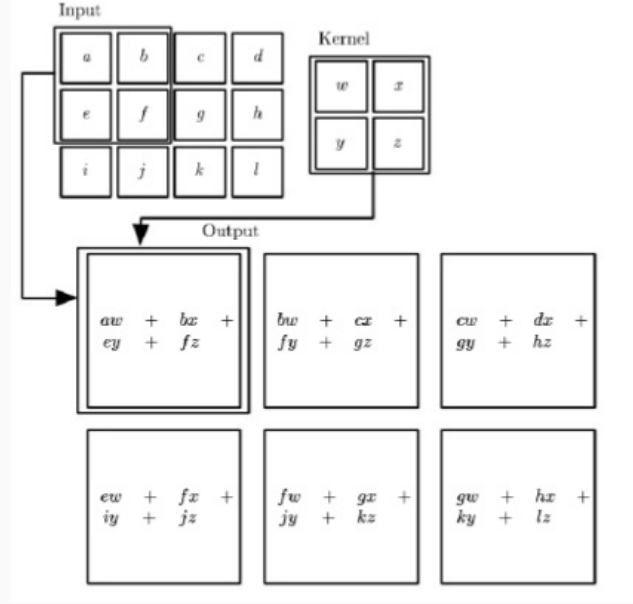
1.3 Local Connections
Come già discusso, l'idea di base delle convolutional neural networks è quella di limitare la complessità delle rete neurale andando ad imporre che i layers di un certo livello sono connessi solamente in modo parziale ai neuroni del layer precedente.
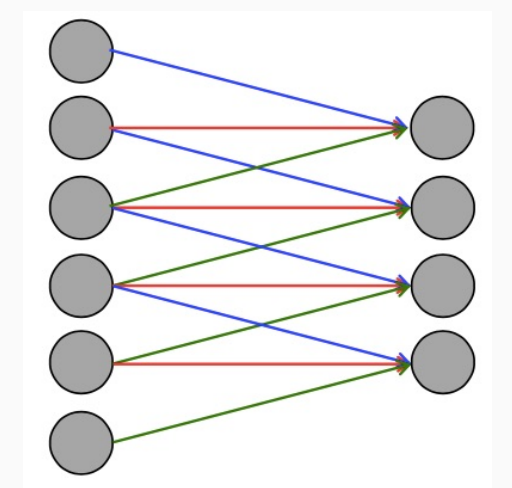
Notiamo che il coefficiente che rappresenta il numero di queste connessioni locale è sempre lo stesso, in quanto il filtro che scorre è sempre lo stesso.
1.4 ConvNet Structure
Le convolutional neural networks sono molto spesso abbreviate con il termine ConvNet.
Concettualmente I neuroni in una ConvNet sono disposti in uno spazio tridimensionale con altezza, larghezza e profondità.
1.5 Types of Layers
Una semplice ConvNet è una sequenza di layers in cui ogni layer trasforma un volume di attivazioni in un'altro volume tramite una funzione differenziabile.
Tipicamente abbiamo tre tipologie di layers:
Convolutional layer
Pooling layer
RELU layer
Fully-Connected layer
Il primo (convolutional) e l'ultimo (fully-connected) effettuano la loro trasformazione utilizzando dei coefficienti che devono essere appressi durante l'apprendimento.
I layer RELU/POOL non hanno coefficienti associati e rappresentano delle semplici operazioni che vengono eseguite sui dati, e dunque non devono essere appressi.
1.6 Example: ConvNet for CIFAR-10
Come esempio di una ConvNet che può essere utilizzata per classificare le immagini nel dataset CIFAR-10 possiamo utilizzare una rete con la seguente architettura
\[[\text{INPUT} - \text{CONV} - \text{RELU} - \text{POOL} - \text{FC}]\]
in cui i vari layers sono così descritti:
\(\text{INPUT}\): Strato dato da un volume \([32 \times 32 \times 3]\) contenente i valori raw dei pixel delle immagini di dimensioni \(32 \times 32\) con un colore a tre canali \(\text{R}, \text{G}, \text{B}\).
\(\text{CONV}\): Strato di convoluzione che trasforma il volume precedente in un volume diverso, che possiamo essere \([32 \times 32 \times 12]\) se decidiamo di utilizzare \(12\) filtri.
\(\text{RELU}\): Su ognuno dei valori ottenuti precedentemente dalla convoluzione applico una funzione di attivazione, come ad esempio la \(\max{(0, x)}\). Il volume rimane quindi invariato.
\(\text{POOL}\): Lo strato di pooling effettua un downsampling, andando a ridurre la dimensione del volume di input effettuando delle operazioni locali sul volume in input. Funzioni tipiche sono la somma o il massimo. Alla fine il volume di output diventa \([16 \times 16 \times 12]\).
\(\text{FC}\): L'ultimo layer è un layer fully-connected che viene utilizzato per calcolare i pesi, ovvero i valori associati alle classi che eventualmente saranno interpretati come valori di probabilità. Il volume di output di questo layer è quindi \([1 \times 1 \times 10]\), dove \(10\) è il numero di classi possibili. Ciascun neurone di questo layer è connesso ad ogni neurone del layer precedente.
Come è possibile vedere quindi, una architettura di tipo ConvNet è una lista di layers che trasformano volumi di input in volumi di output.
2 Convolutional Layer
Il convolutional layer è il layer che effettua l'operazione di convoluzione vista prima

L'idea è quella di considerare un insieme di posizioni sul volume di input e applicare su ogni posizione un filtro, definito da un insieme di coefficienti organizzati tramite una matrice, e il risultato ottenuto sarà un valore associato ad un elemento nel volume di output.
I coefficienti del filtro sono comuni per tutte le unità dei layer. Tutte le unità del layer quindi eseguono le stesse operazioni, ma con l'unica differenza che le eseguono su regioni diverse, ovvero ogni unità lavora su una diversa posizione del volume di input.
2.1 Depth and Stride
L' \(r\) esimo layer convoluzionale dispone i suoi neuroni in tre dimensioni: ampiezza, altezza e profondità. Se assumiamo che il layer \(r\) esimo restituisce un volume di dimensione \(w \times h \times d\), che può essere interpretato come una immagine di dimensione \(w \times h\) in cui ad ogni pixel sono associati \(d\) valori distinti, allora ogni layer di una ConvNet trasforma il volume 3D in input in un diverso volume 3D.
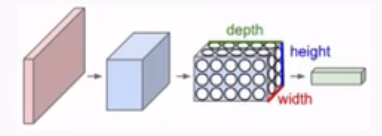
La struttura del layer \(r+1\) (e il suo output) è caratterizzato da due iper-parametri:
Depth: il numero di layers (features) da derivare, che corrisponde al numero di filtri da utilizzare, ciascuno utilizzato per guardare a qualcosa di diverso nell'input.
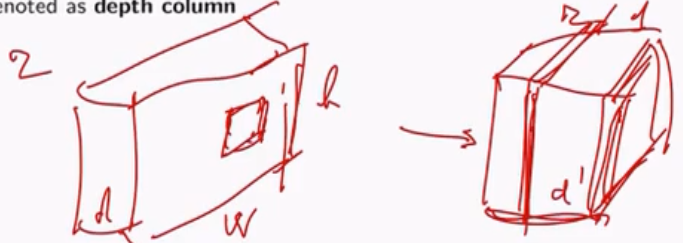
Ogni regione di input viene vista da \(d^{'}\) neuroni diversi, ciascuno che utilizza un diverso filtro.
Stride: il valore di shift utilizzato per spostare il filtro da una regione alla successiva. Quando è \(r = 1\) i filtri sono mossi un pixel per volta, e la width e la height del layer \(r+1\) sono rispettivamente \(w\) e \(h\), ovvero quelli del layer \(r\). Quando è \(k\) ogni volta che i filtri sono mossi \(k\) pixels vengono saltati. Più è grande la stride e più piccolo sarà il volume di output rispetto a quello di input.
Per gestire eventuali edge-cases in cui ci troviamo al bordo, l'idea è quella di assumere una zona di zero-padding ritornata dal layer \(r\). La dimensione di questo zero-padding è un iperparametro del modello.
È possibile dimostrare che il numero di neuroni del layer successivo è calcolato in funzione del numero di neuroni nel layer precedente \((w)\), della dimensione del filtro \((f)\), dello stride \((s)\) e di quanto zero padding viene utilizzato \((p)\) ai bordi. La formula corretta in particolare è la seguente
\[\frac{w - f + 2p}{s}\]
Ad esempio, se ho un input \(7 \times 7\) e un filtro \(3 \times 3\) con stride \(1\) e senza padding, allora ottengo un output \(5 \times 5\), ovvero sto definendo \(25\) posizioni diverse su uno strato del layer successivo.
2.2 Connections Between Layers
Assumiamo che l'input del layer \(r+1\) ha un volume di \(32 \times 32 \times 3\). Assumiamo inoltre di after una filter window size di \(3 \times 3\).
Ciascuna unità nel layer \(r+1\) ha quindi \(3 \times 3 \times 3 + 1 = 28\) valori come input, includendo il bias.
Assumendo poi uno stride \(s=1\), il numero di neuroni in ognuno degli strati del layer \(r+1\) è \(16\). Dato che ogni ogni neurone ha associati \(28\) valori, in totale avremmo \(16 \times 16 \times 28\) collegamenti.
Se poi assumiamo che \(5\) features sono estratte dall'input, allora il numero di unità è \(16 \times 16 \times 5 = 1280\), ognuno con \(28\) coefficienti entranti.
2.3 Real-World Example
todo.
2.4 Summary
todo.
3 Pooling Layer
todo.
4 RELU Layer
5 Layer Patterns