ML - 27 - Deep Learning III
Lecture Info
Date:
Lecturer: Giorgio Gambosi
Slides: (ml_12_deep-slides.pdf)
In questa lezione abbiamo visto le recurrent neural networks, con una loro particolare specializzazione rappresentata dalle Long short term memory networks.
1 Recurrent Neural Networks
Le reti ricorsive (o ricorrenti) vengono utilizzate in tutti quei problemi che necessitano l'elaborazione di sequenze di valori o segnali. Al posto di avere dei vettori di dimensione finita su cui lavorare quindi, in questa tipologia di problemi abbiamo delle sequenze di lunghezza indefinita.
Alcuni problemi affrontati dalle reti neurali in questo contesto sono:
Sequence classification:
sentiment analysis.
DNA sequence classification.
action recognition.
Sequence synthesis:
text
music
Sequence-to-sequence translation:
speech recognition
text translation
PoS tagging
1.1 Sequential Data
Ci sono svariati modi in cu possiamo modellare dei dati sequenziali. Tra questi troviamo:
A partire da una distribuzione \(p(x_1, \ldots, x_n)\) generiamo una sequenza di dati.
Data un'immagine \(I\) vogliamo generare una sequenza di dati per descrivere l'immagine, \(p(y_1, \ldots, y_T | I)\) con \(T\) non predefinito.
A partire da una sequenza di valori e vogliamo determinare un singolo valore \(p(y|x_1, \ldots, x_T)\).
A partire da una sequenza vogliamo derivare una diversa sequenza \(p(y_1, \ldots, y_T|x_1, \ldots, x_T)\). (speech recognition; object tracking).
Generare delle frasi che descrivono un video \(p(y_1, \ldots, y_T^{'}|x_1, \ldots, x_T)\).
Concettualmente possiamo dividere le tipologie di reti ricorrenti in base a come lavorano con le sequenze di dati

Nel primo caso abbiamo una rete che per ogni elemento della sequenza in input genera un elemento della sequenza in output.
Nel secondo caso invece abbiamo che per ogni elemento della sequenza in input la rete genera più elementi della sequenza in output.
In generale poi la sequenza interna generata dalla rete può essere più lunga della sequenza in input/output.
1.2 RNN Network Structure
A differenza delle reti MLP e CNN, le RNN restituiscono per ogni vettore in input un vettore in output. Il valore in output che viene restituito è funzione sia del valore in input che di uno stato interno della rete che contiene informazione su tutti i valori in input precedenti.
Concettualmente la struttura di una RNN è mostrata a seguire
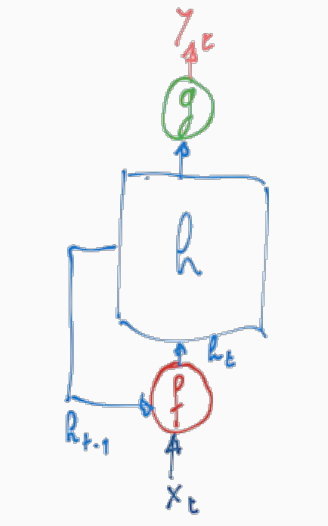
dove \(h\) rappresenta lo stato della rete, e ad ogni istante di tempo \(t\) lo stato viene aggiornato andando a combinare tramite \(f\) lo stato attuale \(h_{t-1}\) con il nuovo input \(x_t\) per formare il nuovo stato \(h_t\). Ad ogni istante di tempo poi la rete produce un valore di output \(y_t\) ottenuto applicando la funzione \(g\) allo stato attuale della rete \(h_t\). In formula quindi troviamo
\[\begin{split} h_t &= f(h_{t-1}, x_t) \\ y_t &= g(h_t) \\ \end{split}\]
1.2.1 Computing Recurrent States
Data una sequenza \(x\) e uno stato iniziale \(h_0\), il modello iterativamente calcola la sequenza di stati ricorrenti
\[h_t = f(x_t, h_{t-1}) = \phi(w_1 x_t + w_2h_{t-1} + b), \,\,\,\,\,\, t = 1, \ldots, T(x)\]
dove tipicamente \(f\) è calcolata applicando una funzione logistica (non-lineare) \(\phi\) ad una combinazione lineare tra \(x_t\) e \(h_{t-1}\) ottenuta definendo delle matrici di pesi \(w_1, w_2\) che vengono imparati tramite la backpropagation.
1.2.2 Computing Output Value
Il valore in uscita invece può essere calcolato ad ogni istante di tempo a partire dallo stato ricorrente nel seguente modo
\[y_t = g(h_t; w) = \psi(w_3 h_t + b^{'})\]
dove \(\psi\) è una funzione che dipende dalla task affrontante. Tipicamente a questo scopo si utilizza una softmax.
1.2.3 Folded/Unfolded Rappresentations
Andando quindi ad esplicitare le funzioni \(f\) e \(g\) otteniamo la seguente struttura
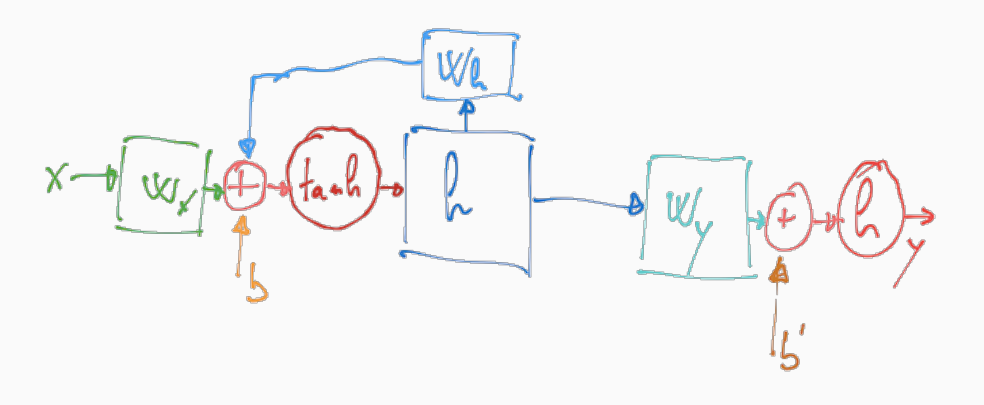
Questa rappresentazione è detta folded in quanto viene mostrato esplicitamente che lo stato all'istante \(t-1\) viene utilizzato per calcolare lo stato all'istante \(t\).
La stessa struttura può essere rappresentata in un altro modo, chiamato unfolded, in cui per ogni istante di tempo andiamo a considerare una diversa rete neurale in cui il valore dello stato di input deriva dalla rete precedente.
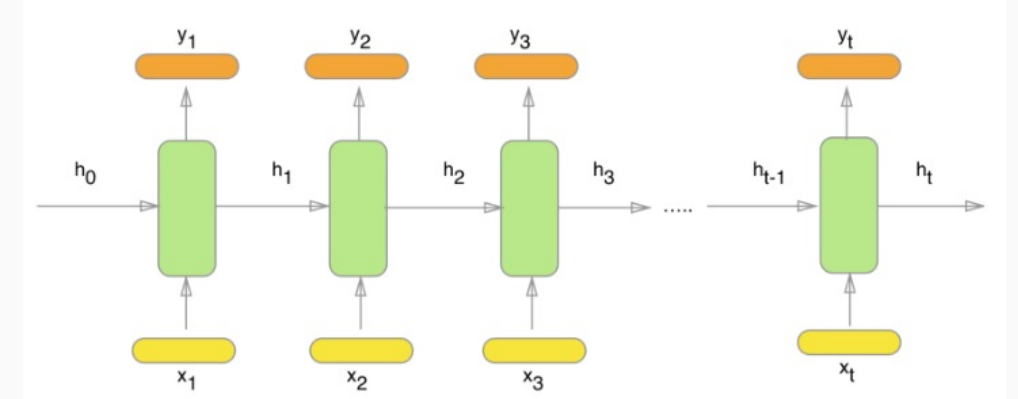
1.3 Learning
Per quanto riguarda l'apprendimento, si può procedere applicando il solito schema che abbiamo visto quando abbiamo trattato la backpropagation.
Detto questo, proprio per il fatto che il numero di layers di un RNN è indefinito, piuttosto che applicare esattamente la tecnica già vista, l'idea è quella di adattare la backpropagation a situazioni di questo tipo tramite un meccanismo noto con il nome di Backpropagation through time (BPTT).
2 LSTM Networks
Le RNN presentano dei problemi nel caso in cui il valore restituito in un certo istante deve dipendere anche da valori che sono stati dati in input alla rete in un tempo significativamente precedente. In formula quando il valore di output \(y_t\) dipende molto dal valore di input \(x_t^{'}\), con \(t^{'} << t\). Questo problema è una conseguenza del vanishing gradient.
Per gestire questo problema sono state definite le reti di tipo Long Short Term Memory (LSTM), che sono dei particolari tipi di RNN che introducono dei particolari layer che si specializzano per mantenere una informazione di lunga durata.
2.1 First Version
Un esempio di LSTM è il seguente
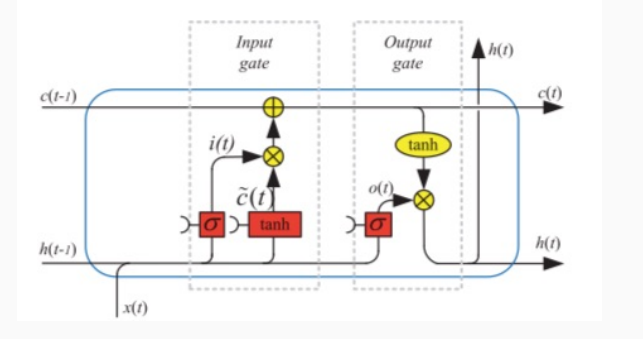
dove \(x(t)\) rappresenta l'input al tempo \(t\), \(h(t-1)\) è lo stato precedente della rete, e \(c(t-1)\) è la componente di memoria a lungo termine.
Come è possibile vedere, la LSTM opera in due fasi successive, che prendono il nome di input gate e output gate. L'input gate serve a determinare come modificare il contenuto della memoria a lungo termine. Lo stato di output invece specifica come ottenere l'output della rete utilizzando l'input \(x(t)\) e lo stato della memoria aggiornata.
2.1.1 Input Layer
L'input gate è schematizzato nel seguente modo: prima si esegue la seguente unità
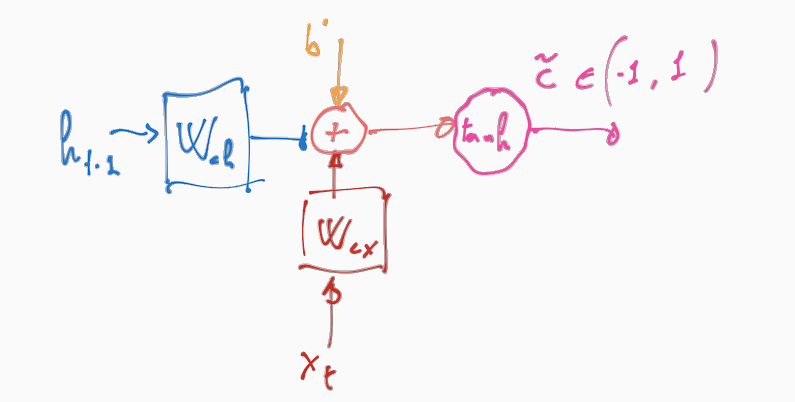
Come possiamo vedere prende in input tre valori: lo stato precedente \(h(t-1)\), il valore di input \(x(t)\) un valore di bias \(b_c\). Una volta combinati tra loro questi valori, viene applicata la tangente iperbolica per riportare gli elementi nel vettore risultante a valori tra \(-1\) e \(1\). Il vettore ottenuto dall'applicazione della tangente iperbolica rappresenta una proposta di aggiornamento per il vettore che rappresenta la memoria a lungo termine.
Continuando, si esegue anche quest'altra unità, analoga quella precedente
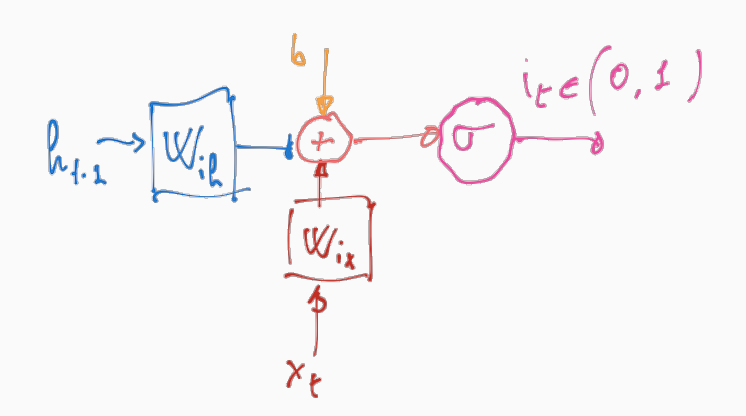
Il vettore ottenuto da questa operazione viene permette ad assegnare un peso che regola l'aggiornamento di ogni cella di memoria.
Alla fine quindi l'update della memoria locale è ottenuta andando ad incrementare ciascuna cella per i valori contenuti in \(\tilde{C}_t\) che sono scalati dai pesi in \(i_t\). In formula,
\[\begin{split} i_t &= \sigma(w_{i,h} \cdot h_{t-1} + w_{i,x} \cdot x_t + b_i) \\ \tilde{C}_t &= \tanh{(w_{c,h} \cdot h_{t-1} + w_{c,x} \cdot x_t + b_c)} \\ C_t &= C_{t-1} + i_t \boldsymbol{\cdot} \tilde{C}_t \\ \end{split}\]
2.1.2 Output Layer
L'output layer invece è così descritto
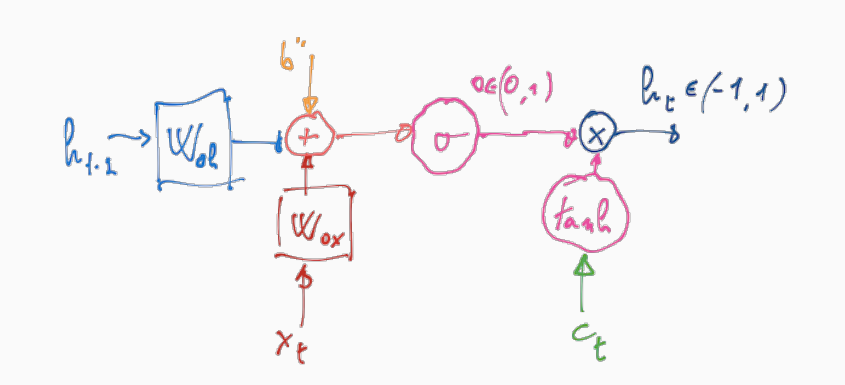
in formula,
\[\begin{split} o_t &= \sigma(w_{o,h} \cdot h_{t-1} + w_{o,x} \cdot x_t + b_0) \\ h_t &= o_t \boldsymbol{\cdot} \tanh{(C_t)} \\ \end{split}\]
2.2 With Forget Layer
Una seconda versione delle LSTM può essere ottenuta tramite l'introduzione di un forget gate layer. Il ruolo di questo ulteriore layer è quello di determinare la decrescita della rilevanza delle celle di memoria rispetto all'input attuale e alla storia precedente.
La struttura generale di una LSTM è la seguente
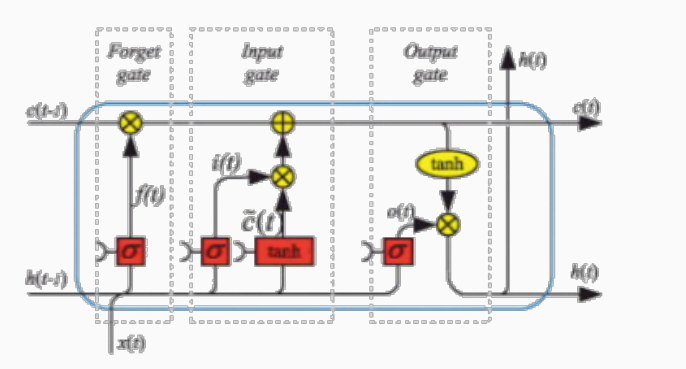
Come è possibile vedere, il forget layer aggiorna il contenuto della memoria tramite la funzione \(f_t\)
\[f_t = \sigma(w_{f,h} \cdot h_{t-1} + w_{f,x} \cdot x_t + b_f)\]
La nuova memoria sarà quindi calcolata nel seguente modo, tenendo anche in considerazione il valore di \(f_t\)
\[C_t = f_t \boldsymbol{\cdot} C_{t-1} + i_t \boldsymbol{\cdot} \tilde{C}_t\]
2.3 Variants
2.3.1 Peephole
Nelle LSTM viste finora il valore delle celle di memoria andava ad influire solamente lo stato successivo della rete, e non veniva utilizzato direttamente per determinare l'individuazione dei valori nei vari gates.
L'idea è quindi quella di introdurre la struttura LSTM con peephole, schematizzata come segue
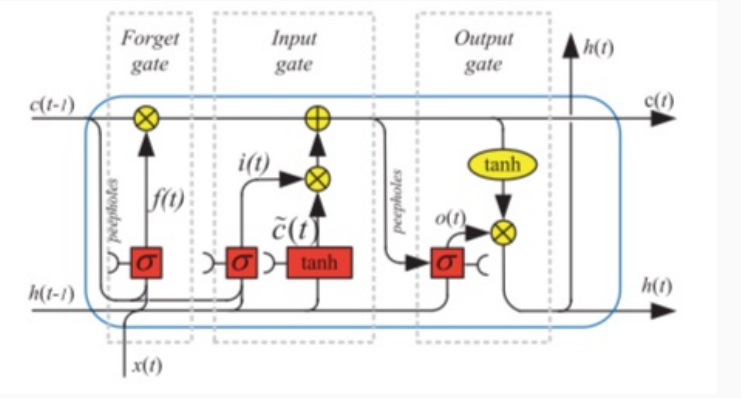
2.3.2 GRU
Descritta come segue
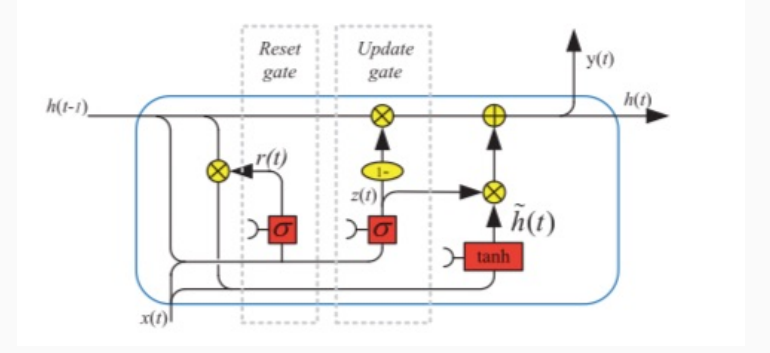
3 Topologies
Le celle ricorrenti (in particolare nelle LSTM) possono essere collegate tra loro secondo diverse tipologie. Tra queste troviamo:
Stacked networks.
bidirectional networks.
Multidimensional networks.
Graph networks.