ML - 28 - Decision Trees
Lecture Info
Date:
Lecturer: Giorgio Gambosi
Slides: (ml_13_dectrees-slides.pdf)
In questa lezione abbiamo discusso gli alberi di decisione (decision trees), che sono dei metodi che possono essere utilizzati per effettuare sia la regressione che la classificazione, e che sono basati sul decomporre in modo ricorsivo lo spazio delle features.
1 Structure
La decomposizione ricorsiva dello spazio viene rappresentata tramite un albero.

L'albero è caratterizzato nel seguente modo:
La radice dell'albero rappresenta l'intero spazio delle istanze.
I nodi interni dell'albero rappresentano regioni dello spazio delle istanze, e il passaggio da un nodo padre al successivo nodo figlio corrisponde ad una partizione della regione corrispondente al nodo padre. In corrispondenza di ogni passaggio padre-figlio quindi dobbiamo specificare come viene effettuata la partizione dello spazio. Tipicamente questo avviene in funzione dei valori degli attributi.
Ogni foglia è associata ad un sottospazio che non è ulteriormente partizionato. Per ogni foglia viene quindi specificata una classe, la classe predetta per tutti gli elementi che finisco in quella regione.
2 Usage
Una volta che abbiamo un albero di decisione la procedura per effettuare classificazione è la seguente: si parte dalla radice e si scende lungo l'albero andando di volta in volta a prendere il path rispetto ai criteri di partizionamento e al valore delle features dell'elemento che vogliamo classificare. Alla fine arriviamo ad una foglia, e associamo all'elemento la classe associata alla foglia.
Più formalmente, dato un elemento \(\mathbf{z} = (z_1, \ldots, z_d)^T\), per effettuare la classificazione l'albero di decisione viene attraverso partendo dalla radice.
Ad ogni nodo attraverso è associata una feature \(x_i\) e una funzione \(f_i\). Per decidere il nodo successivo da considerare tra l'insieme dei nodi figli viene calcolato il valore \(f_i(z_i)\). Un caso particolare è quando si definisce un valore di treshold \(\theta_i\), che viene confrontato con il valore \(z_i\) per capire quale nodo successivo considerare.
La procedure termina quando si raggiunge un nodo foglio, e il valore ritornato è dato dalla classe corrispondente, o viene derivata a partire dal vettore che contiene le probabilità delle classi (nell'esempio precedente il valore della lista value).
3 Example: Iris Dataset
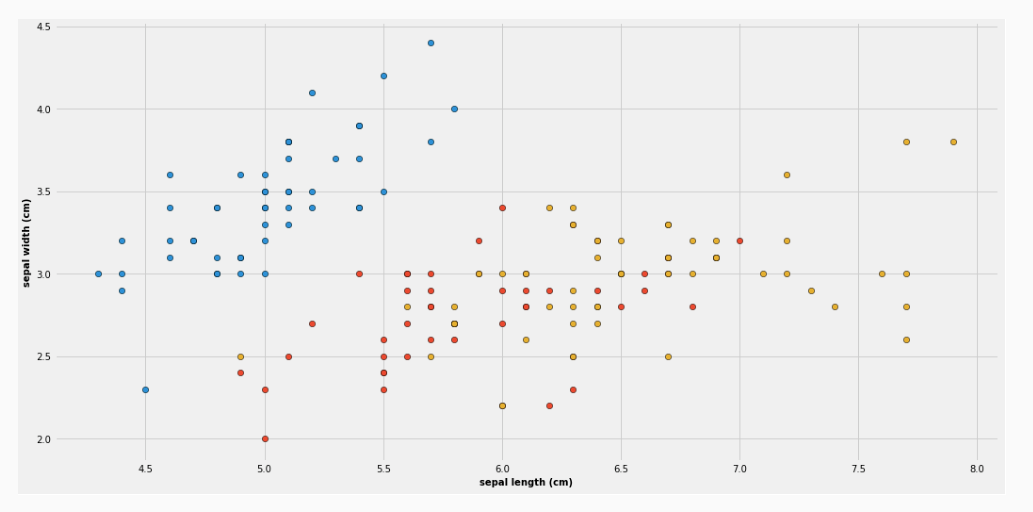
Consideriamo ad esempio la seguente proiezione del famoso dataset iris, in cui considero solamente due features: la sepal length e la sepal width. In totale abbiamo tre classi, rappresentati dai vari colori.
Il primo livello dell'albero di decisione è così rappresentato

Il valore values rappresenta la distribuzione degli elementi nelle varie classi. La prima riga rappresenta invece la condizione utilizzata per effettuare la partizione. In questo caso l'attribuzione finale è effettuata in base alla classe che nel training set contiene più elementi. Tale nodo rappresenta la seguente partizione
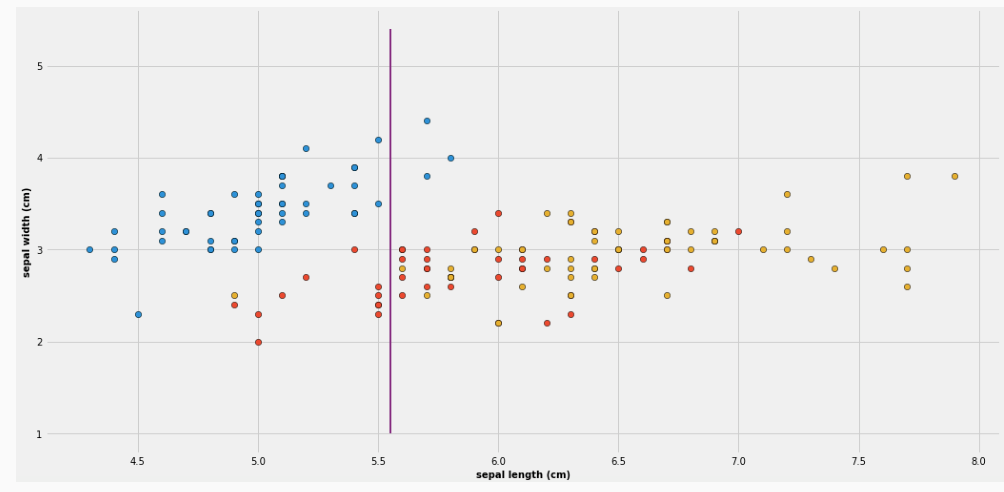
Continuando, l'albero può essere esteso nel seguente modo
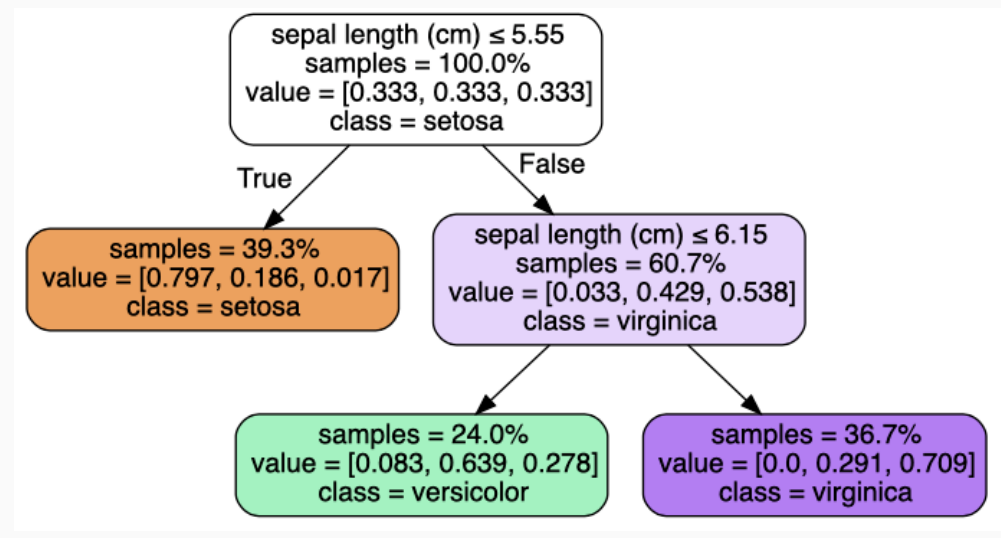
che visivamente corrisponde alla seguente partizione
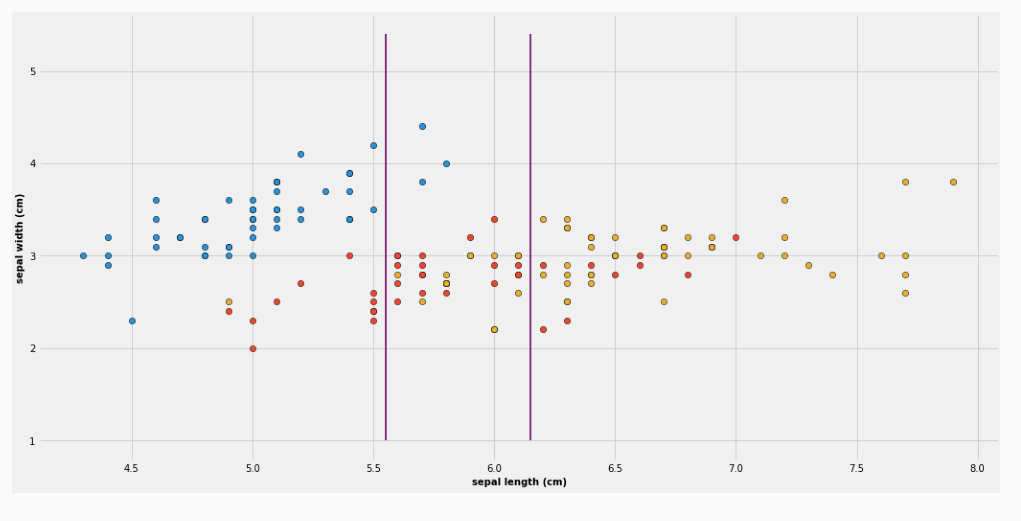
Continuando ad iterare questa struttura otteniamo
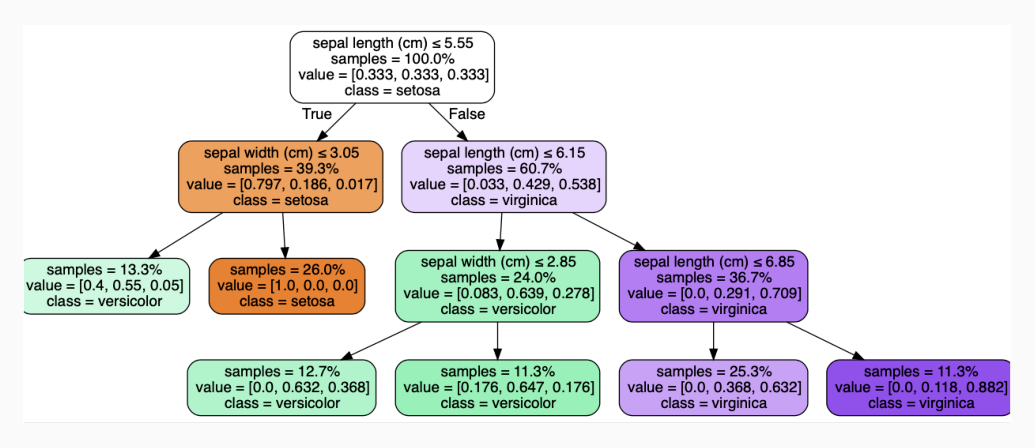
che corrisponde alla seguente partizione
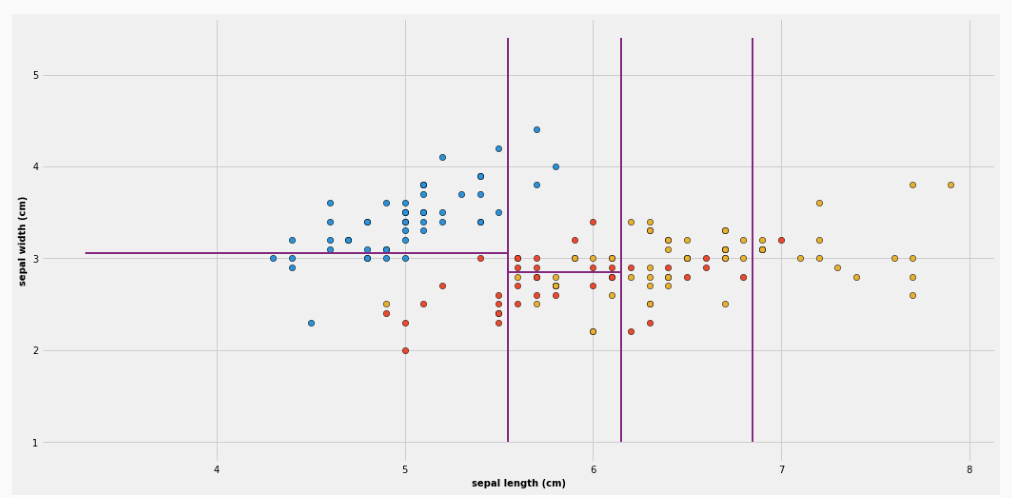
4 Pros/Cons
I decision trees presentano le seguenti caratteristiche interessanti:
Hanno una struttura molto semplice.
Applicando un albero di decisione per classificare un elemento è un processo "trasparente", ovvero siamo in grado di stabilire il perché quell'elemento è stato classificato in quella classe. Questa proprietà è detta explainability, e tipicamente è molto difficile da ottenere quando si utilizzano modello di tipo rete neurale.
Una problema dei decision tree però è che tendono andare facilmente in overfitting. Questo fatto dipende molto dal modo in cui sono costruiti.
5 Construction
Come abbiamo già detto, gli alberi di decisione sono costruiti andando a partizionare in modo ricorsivo lo spazio delle features.
Ad ogni nodo dell'albero dobbiamo quindi porci le seguenti domande:
Come effettuiamo la partizione della corrispondente regione dello spazio delle features? Ovvero come sceltio la feature \(x_i\) e la funzione \(f_i\) con cui effettuare questa partizione?
Quando fermiamo la nostra partizione? Ovvero quando arriviamo ad un nodo foglio?
Non appena scegliamo di fermare il partizionamento, e quindi quando siamo arrivati ad una foglia del nostro albero di decisione, come scegliamo la classe da assegnare alla foglia?
Observation: La struttura finale dell'albero di decisione è la stessa sia nel caso della classificazione che nel caso della regressione. L'unica cosa che cambia è la procedura di costruzione.
5.1 Partinioning
Supponiamo adesso di considerare un nodo e di volerlo partizionare. L'idea è quella di andare a selezionare la feature e la soglia tali che una determinata misura è massimizzata nell'intersezione del training set con ognuna delle sottoregioni ottenute dalla partizione. Questa misura è una misura di impurità, e deve essere minimizzata.
Per fare questo abbiamo bisogno di una inpurity measure.
5.2 Impurity Measure
Consideriamo una v.a. discreta con dominio \(\{a_1, \ldots, a_k\}\) e corrispondenti probabilità \((p_1, \ldots, p_k)\). Una misura di impurità \(\phi:p \to \mathbb{R}\) deve soddisfare le seguenti probaiblità
\(\phi(p) \geq 0\) per ogni possibile \(p\)
\(\phi(p)\) è minimo se esiste un \(i\) con \(1 \leq i \leq k\) tale che \(p_i = 1\)
\(\phi(p)\) è massimo se \(p_i = 1/k\) per ogni \(i\)
\(\phi(p) = \phi(p^{'})\) per ogni \(p^{'}\) derivanti da una permutazione di \(p\)
\(\phi(p)\) è differenziabile in ogni punto
Intuitivamente più le probabilità sono le stesse e maggiore è l'inpurità.
5.3 Goodness of split
Nel nostro caso consideriamo la classe di ogni elemento in \(S\). In particolare per ogni insieme \(S\) di elementi, il vettore delle probabilità associato ad \(S\) può essere ottenuto nel seguente modo
\[p=\Bigg(\frac{|S_1|}{S|}, \ldots, \frac{|S_k|}{|S|} \Bigg)\]
dove \(S_h \subseteq S\) è l'insieme di elementi in \(S\) appartenenti alla classe \(C_h\).
Data una funzione \(f\) che suddivide gli elementi di \(S\) in \(r\) sottoinsiemi diversi, formalmente \(f: S \to \{1, \ldots, r\}\). Sia \(s_i\) l'insieme degli elementi che vengono mappati al valore \(i\) da \(f\), formalmente \(s_i = \{x \in S: \,\, f(x) = 1\}\).
Definiamo il goodness of split (bontà) di \(S\) rispetto ad \(f\) tramite la seguente quantità
\[\Delta_{\phi}(S, f) = \phi(p_S) - \sum\limits_{i = 1}^r p_i \phi(p_{s_i})\]
dove \(\phi\) è una funzione di impurità.
Come possiamo vedere quindi, la bontà di un partizionamento è ottenuta calcolando la differenza tra l'impurità dell'insieme di partenza \(S\) con la somma delle impurità dei sottoinsiemi ottenuti applicando \(f\).
In pratica \(f\) è definita andando a considerare una sola feature. A seconda della tipologia di feature abbiamo due casi diversi:
Se la feature è discreta, la partizione viene effettuata andando a partizionare l'insieme dei suoi possibili valori.
Se la feature è continua invece la partizione viene effettuata applicando un valore di soglia.
5.4 Gini Index
Un modo per misurare l'impurità è attraverso il gini index
\[G_S = 1 - \sum\limits_{i = 1}^k \Bigg(\frac{|S_i|}{|S|} \Bigg)^2\]
5.5 Entropy as Impurity Measure
Per ogni insieme di elementi \(S\), sia
\[H_S = -\sum\limits_{i = 1}^k \frac{|S_i|}{|S|} \log_2{\frac{|S_i|}{|S|}}\]
l'entropia di \(S\).
Utilizzando l'entropia come misura di impurità, il goodness of split è dato dall'information gain. Data una funzione di partizione \(f\), l'information gain è definito nel seguente modo
\[\text{IG}(S, f) = H_S - \sum\limits_{j = 1}^r \frac{|s_j|}{|S|}H_{s_j}\]
5.6 Other Measures of Impurity
todo.
5.7 When to Stop
todo.
Necessitiamo di condizioni che stabiliscono quando dobbiamo fermare la partizione.
5.8 Pruning
todo