ML - 29 - Ensemble Methods
Lecture Info
Date:
Lecturer: Giorgio Gambosi
Slides: (ml_14_ensemble-slides.pdf)
In questa lezione abbiamo introdotto i metodi ensemble, parlando in particolare del bagging e del boosting.
1 Ensemble Methods
L'impostazione seguita dai metodi ensemble è quella di utilizzare un insieme di classificatori non particolarmente efficaci, che prendono il nome di weak learners, coordinando i vari risultati per ottenere una risposta finale complessiva più efficace.
Per fare questo ci sono due approcci generali:
Bagging: consiste nel formare un comitato (committee) di \(L\) versioni diverse dello stesso tipo di classificatori, utilizzare questi modelli per effettuare \(L\) predizioni diverse, e infine combinarle per ottenere la predizione complessiva globale.
Boosting: L'idea è quella di addestrare diversi modello dello stesso tipo in sequenza, dove la funzione di errore per addestrare un particolare modello viene calcolata in funzione della performance dei modelli precedentemente addestrati.
2 Bagging
Il bagging parte utilizzando dei classificatori che presentano una elevata varianza, ovvero che il modo in cui classificano gli elementi cambia molto se si cambia leggermente il training set con cui apprendono.
Un esempio di classificatori che presentano questo tipo di comportamento sono i decision trees, in quanto il partizionamento dello spazio effettuato ad un dato livello influenza i successivi partizionamenti, e quindi se i dati sono leggermente diversi e questo porta ad una piccola modifica nel modo in cui lo spazio delle features è partizionato ad un certo livello, allora questa differenza si farà sentire nei livelli più bassi.
Il bagging può quindi essere visto come un metodo che compone risultati finalizzato a diminuire la varianza della classificazione.
2.1 Bootstrap Sample
Il bagging utilizza un metodo più generale utilizzato nella statistica e noto con il nome di bootstrap. Il bootstrap è un metodo di resampling, e consiste nel partire da un insieme di elementi a nostra disposizione ed estrarre da questo insieme un certo numero \(K\) di sottoinsiemi.
Dato un insieme di training data \((x_i, t_i)\), \(i=1,\ldots,n\), l'idea è quella di calcolare la funzione di distribuzione empirica \(\hat{\mathcal{F}}\), definita come segue
\[\hat{p}(x, t) = \begin{cases} \frac{1}{n} &,\,\, \exists i: \,\, (x, t) = (x_i, t_i) \\ 0 &,\,\, \text{ otherwise} \\ \end{cases}\]
Notiamo come questa è una distribuzione di probabilità discreta, in cui ad ogni training point è associato un peso di \(1/n\).
Fissato un certo \(m\), in cui tipicamente (ma non necessariamente) \(m \leq n\), un bootstrap sample di size \(m\) è un insieme formato dai seguenti elementi
\[(x_i^*, t_i^*) \,\,\,\, i = 1,\ldots, m\]
dove ogni \((x_i^*, t_i^*)\) è estratto in modo uniforme dal training set \((x_1, t_1), \ldots, (x_n, t_n)\) con replacement.
Questo processo corrisponde ad estrarre \(m\) valori dalla distribuzione \(\hat{\mathcal{F}}\), e per questo quanto ottenuto approssima quello che otterremmo se potessimo estrarre valori dalla vera distribuzione \(\mathcal{F}\). Molto spesso consideriamo il caso \(m=n\), che consiste nel campionare un intero nuovo training set.
Tramite questa procedura quindi a partire dal training set con \(n\) elementi riusciamo a costruirci \(k\) insiemi di \(n\) elementi indipendenti tra loro.

Osservazione: Il fatto di imporre un replacement rende le estrazioni indipendenti tra loro, e questo ci permette di trasfrire la proprietà i.i.d. del training set originale al bootstrap sample.
2.2 Usage
Dato un training set \((x_i, y_i)\), \(i=1,\ldots,n\), il bagging consiste nel calcolare la media delle predizioni ottenuta da classificatori dello stesso tipo (tipicamente alberi di decisione) rispetto ad una collezione di bootstrap samples.
In particolare per \(b=1,\ldots,B\), \(n\) bootstrap items \((x_i^b, y_i^b)\), \(i=1,\ldots,n\) sono generati e un classificatore viene addestrato su questi dati.
Alla fine, dopo che tutti i \(B\) classificatori sono stati addestrati, per classificare un input \(x\) andiamo ad utilizzare questi \(B\) classificatori e assegnamo a \(x\) la classe più predetta tra tutti i classificatori.
Nel caso della regressione invece, il valore predetto viene derivato effettuando l'average tra tutti i valori ritornati dai \(B\) regressori.
2.3 Variant
Se il classificatore viene utilizzato per ritornare il vettore di probabilità delle classi \(\hat{p}_k^b(x)\), il risultato finale complessivo è ottenuto nel seguente modo
\[p_k(x) = \frac{1}{B}\sum\limits_{b = 1}^B \hat{p}_k^b(x)\]
come è possibile vedere, la classe predetta è, nuovamente, quella con la maggiore probabilità.
2.4 Why it Works?
Perché il bagging funziona?
L'intuizione è che facendo la media di più classificatori con elevata varianza, la varianza complessiva tende a diminuire.
2.4.1 Classification
Per capire meglio quanto detto vediamo un caso di classificazione binaria. Supponiamo di avere \(B\) classificatori indipendenti, ciascuno con una percentuale di misclassificazione \(e = 0.4\) piuttosto alta. Consideriamo poi un elemento \(x\) da classificare, e assumiamo senza perdità di generalità che la classe di \(x\) è \(1\). Da questo segue che il \(b\) esimo classificatore predice per \(x\) la classe \(0\) con probabilità \(e=0.4\)
Sia \(B_0 \leq B\) il numero di classificatori che misclassificano l'elemento \(x\). Assumendo che i classificatori sono indipendenti tra loro, il valore di \(B_0\) segue una distribuzione binomiale con parametri \(B, e\)
\[B_0 \sim \text{Binomial}(B, e)\]
La misclassification rate del classificatore bagged (quello complessivo) è quindi data da
\[p\Bigg(B_0 > \frac{B}{2} \Bigg) = \sum\limits_{y = B/2 + 1}^B \binom{B}{k}e^k(1 - e)^{B - k}\]
notiamo che quest'ultima quantità tende a \(0\) al crescere di \(B\).
2.4.2 Regressione
Nel caso invece della regressione, l'expected error di un modello \(y_i(x)\) rispetto al valore corretto \(h(x)\) è dato da
\[E_x[(y_i(x) - h_(x))^2] = E_x[\epsilon_i(x)^2]\]
L'average expected error rispetto a tutti i modelli considerati separatamente è dato da
\[E_{\text{av}} = \frac{1}{m} \cdot \sum\limits_{i = 1}^m E_x[\epsilon_i(x)^2]\]
Il committe expected errore invece aggregando le varie risposte tra loro è dato da
\[E_c = E_x\Bigg[\Bigg(\frac{1}{m} \sum\limits_{i = 1}^m y_i(x) - h_(x)\Bigg)^2 \Big] = E_x\Bigg[\Bigg(\frac{1}{m} \sum\limits_{i = 1}^m \epsilon_i(x) \Bigg)^2 \Bigg]\]
Andando a sviluppare il quadrato otteniamo due tipologie di fattori:
Fattori della forma
\[\frac{1}{m^2} \epsilon_i(x)^2\]
che sommati assieme ci danno esattamente \(E_{\text{av}}\) a meno di un fattore di \(1/m\).
E anche fattori della forma
\[\frac{1}{m^2} \epsilon_i(x) \cdot \epsilon_j(x)\]
Se assumiamo quindi che gli errori sono scorrelati tra loro, ovvero che per \(i \neq j\) si ha \(E_x[\epsilon_i(x) \epsilon_j(x)] = 0\), allora otteniamo che
\[E_c = \frac{1}{m^2} \sum E_x[\epsilon_i(x)^2] = \frac{1}{m} E_{\text{av}}\]
E quindi l'errore che ci viene offerto dal regressore bagged è minore di quello ottenuto facendo la media tra tutti gli errori se i modelli sono indipendenti tra loro.
Observation: Questo però funziona solo teoricamente, in quanto è facile vedere che questi diversi modelli sono ottenuti dallo stesso training set, e dunque non sono completamente indipendenti.
2.5 Out-of-Bag Error
Per valutare il risultato di una predizione cumulativa l'idea è quella di valutare, per ogni elemento \(x_i\) del training set, la predizione effettuata dall'insieme di modelli addestrati in bootstrap samples che non includevano l'elemento \(x_i\). Questo tipo di stima dell'errore prende il nome di out-of-bag error.
Questo viene fatto in quanto altrimenti la differenza tra training set e test set sarebbe molto più sottile e sfumata.
Se i bootstrap sample hanno lo stesso size del training set, abbiamo una probaiblità $.63$ che un elemento non è incluso nel bootstrap sample. Per ogni elementi infatti la probabilità che l'elemento non sia selezionato in una singola estrazione è \(1 - 1/n\). Dopo \(n\) estrazioni quindi la probabilità di non essere estratto è \((1 - 1/n)^n\). Notando poi che
\[\lim\limits_{n \to \infty} \Big(1 - \frac{1}{n}\Big)^n = \frac{1}{e} \approx .37\]
Per valori abbastanza grandi di \(n\) abbiamo quindi che un generico elemento \(x\) non sarà stato selezionato dal $.37$ percento dei classificatori.
2.6 Random Forest
Un caso particolare del bagging è rappresentato dalle random forest, che essenzialmente è un insieme (random) di alberi di decisione.
La creazione di una random forest di \(B\) alberi di decisione avviene nel seguente modo:
Per ogni albero \(b = 1,\ldots,B\)
Si genera un botostrap sample dal training set.
Si apprende un albero di decisione \(T_b\) nel bootstrap sample effettuando le seguenti operazioni per ogni nodo:
Si selezionano \(m\) variabili (tra le features) in modo randomico
Si sceglie la "migliore" rispetto a queste \(m\) variabili
Si splitta il nodo in due figli
Alla fine si ritorna la sequenza di alberi \(T_1, \ldots, T_B\)
Una volta che si ha la random forest nel caso della classificazione si procede calcolando la maggioranza, mentre nel caso della regressione si calcola la media rispetto ai valori predetti dai vari alberi di decisione.
3 Bootsting
Il bootsting è una procedura che anch'essa combina molti classificatori deboli (weak learners) al fine di produrre un comitato più potente con prestazioni migliori.
A differenza del bagging, il bootsting produce i classificatori in una sequenza. In particolare quindi viene prodotta una sequenza di weak classificers \(y_j(x)\) per \(j = 1,\ldots, m\) le cui predizioni sono combinate attraverso un meccanismo di votazione pesata.
In un caso di classificazione binaria ad esempio la predizione finale è effettuata nel seguente modo
\[y(x) = \text{sgn}\Big(\sum\limits_{j = 1}^m \alpha_j y_j(x) \Big)\]
Ogni peso \(\alpha_j > 0\) viene calcolato dall'algoritmo di bootsting e riflette quanto accuratamente il classificatore \(y_j\) classifica i dati.
3.1 Adaboost
Ci sono varie tipologie di boosting. Tra queste la più famosa è detta adaboost, per adaptibe boosting. Questo metodo di boosting presenta le seguenti caratteristiche:
I modelli sono addestrati in sequenza, e ogni modello è addestrato utilizzando una versione pesata del training set. Il peso associato ad ogni elemento del trainign set indica quanto rilevante è quell'elemento, ovvero di quanto la misclassificazione di quell'elemento va ad impattare nella funzione di costo.
I pesi per i vari elementi sono calcolati in funzione delle performance dei modelli precedenti. In particolare i punti misclassificati ricevono dei pesi maggiori. Ogni modello viene quindi addestrato con un particolare dataset, ottenuto in funzione dei modelli precedenti.
Le predizioni vengono effettuate tramite uno schema di maggioranza pesata rispetto a tutti i modelli.
Graficamente lo schema di apprendimento in adaboost è così descritto
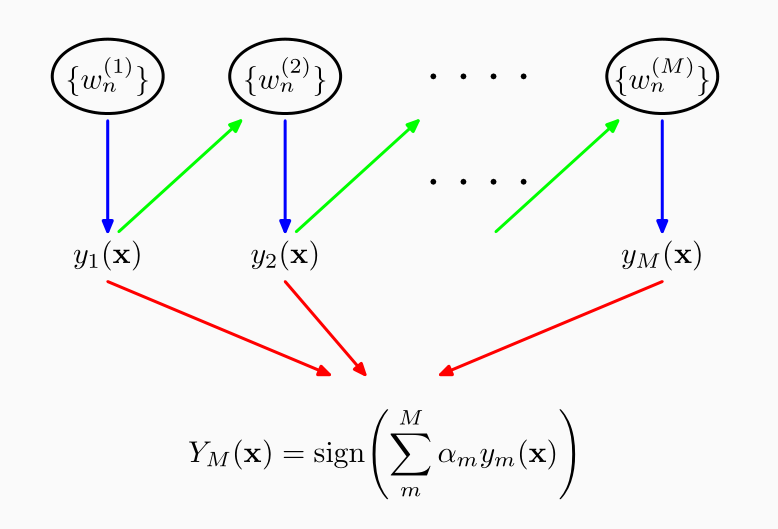
3.1.1 Binary Classification
Consideriamo un caso di classificazione binaria con un dataset \((\mathbf{X}, \mathbf{t})\) di size \(n\), con \(t_i \in \{-1, 1\}\).
L'algoritmo adaboost mantiene un insieme di pesi \(w(x) = (w_1, \ldots, w_n)\) associati ai vari elementi del dataset. L'algorimo procede nel seguente modo:
Si inizializzano i pesi come segue
\[w_i^{(0)} = \frac{1}{n}, \,\,\, i = 1,\ldots, n\]
Per \(j = 1,\ldots,m\)
Si addestra uno weak learner \(y_j(x)\) su \(\mathbf{X}\) in modo da minimizzare la misclassificazione rispetto a \(w^{(j)}(x)\).
Sia quindi
\[e^{(j)} = \frac{\sum\limits_{x_i \in \xi^{(j)}} w_i^{(j)}}{\sum\limits_i w_i^{(j)}}\]
dove \(xi^{(j)}\) è l'insieme degli elementi del dataset classificati male da \(y_j(x)\).
A questo puno se \(e^{(j)} > 1/2\), allora considero il reverse learner, ovvero il classificatore che ritorna la predizione opposta rispetto a quella di \(y_j(x)\) per ogni elementi. Così facendo posso considerare in ogni caso \(e^{(j)}\) come un valore di probabilità, e in particolare lo interpreto come il valore di probabilità che estraendo un elemento random dal training set questo viene classificato male, assumendo che l'elemento \(x_i\) può essere campionato con probabilità \(\frac{w_i^{(j)}}{\sum_i w_i^{(j)}}\).
A partire da \(e^{(j)}\) posso calcolare \(\alpha_j\) nel seguente modo (escludendo il caso limite \(e^{(j)} = 1/2\))
\[\alpha_j = \log{\frac{1 - e^{(j)}}{e^{(j)}}} > 0\]
Infine, per ogni \(x_i\) aggiorno il peso corrispondente come segue
\[w_i^{(j+1)} = \begin{cases} w_i^{(j)} e^{\alpha_j} > w_i^{(j)} &,\,\,\, x_i \in \xi^{(j)} \\ w_i^{(j)} &,\,\,\, \text{ otherwise } \\ \end{cases}\]
notiamo quindi come i pesi degli elementi classificati male dal classificatore \(j\) vengono aumentati per formare il nuovo training set del classificatore \(j+1\).
La predizione finale è quindi ottenuta come segue
\[y(x) = \text{sng}\Bigg(\sum\limits_{j = 1}^m\alpha_j y_j(x) \Bigg)\]
dato che \(y_j(x) \in \{-1, 1\}\), questo corrisponde ad una procedura di voto in cui la predizione di ciascun modello viene pesato rispetto alla confidenza del modello stesso (rappresentata dal coefficiente \(\alpha_j)\).
Notiamo che una bassa learner confidence è inversamente proporzionale alla probabilità di misclassification. Inoltre,
\[w_i^{(t)} = \frac{1}{n} \prod\limits_{j \in \mathcal{B}_i} \frac{1 - e^{(j)}}{e^{(j)}}\]
dove \(\mathcal{B}_i\) è l'insieme dei "bad" weak learners rispetto a \(x_i\), ovvero dei weak learners che misclassificano \(x_i\). Dato che \(1 - e^{(j)} > e^{(j)}\), ne segue che i "bad" learners aumentano l'importanza di un elemento mentre i "good" learners la lasciano invariata.
Così facendo con l'aumentare delle iterazioni ciascun classificatore si deve concentrare nella parte del training set che è stato classificato male dai precedenti classificatori.
3.1.2 Example
Il seguente schema mostra una classificazione binaria in uno spazio bidimensionale tramite adaboost.
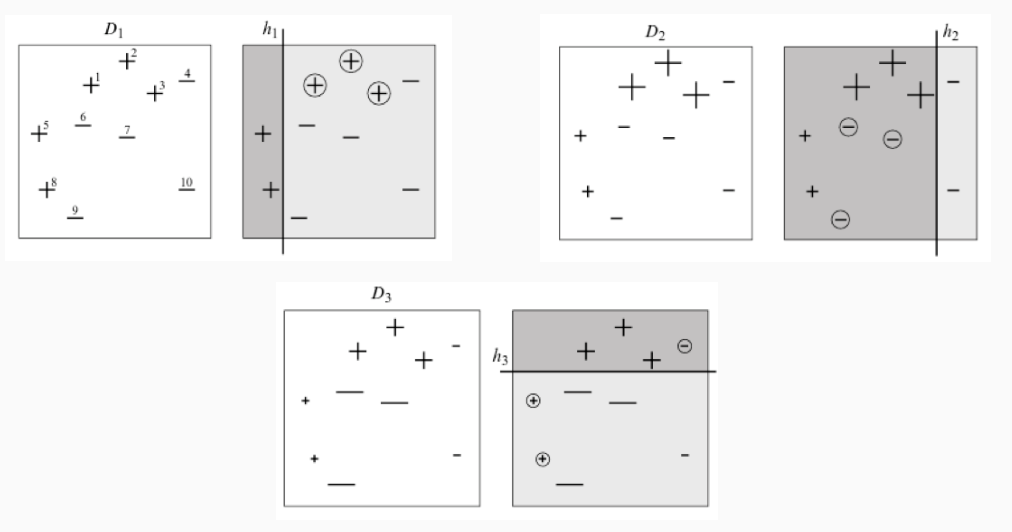
I weak learners utilizzati sono alberi di decisione di altezza 1, ovvero effettuano una sola partizione dello spazio delle features. Questi alberi sono anche detti stamps.
Come è possibile vedere il peso dei vari elementi, caratterizzato dalla dimensione dei simboli \(+, -\), tende ad aumentare quando il classificatore sbaglia predizione, e a diminuire quando effettua correttamente la predizione.
La predizione finale è ottenuta nel seguente modo
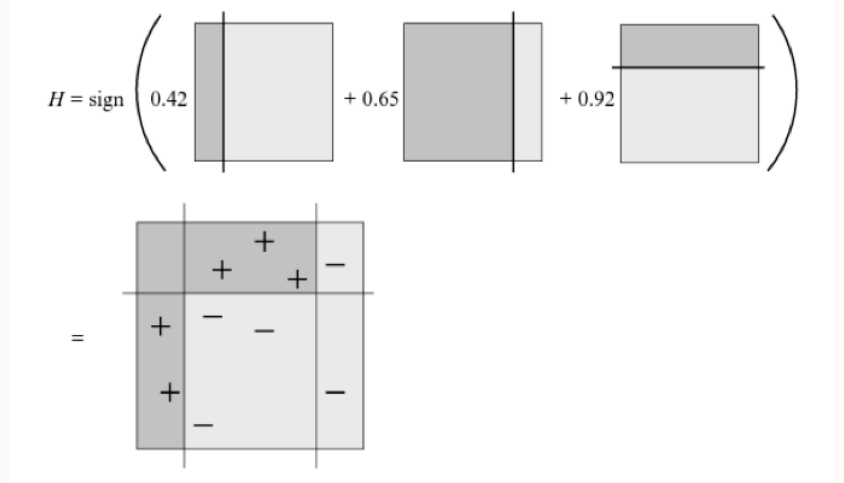
3.2 Additive Models
Adaboost è un caso particolare di un modello additivo, che calcola la predizione sommando predizioni da modelli più semplici
\[y(x) = \sum\limits_{j = 1}^m c_j \overline{y}(x;\mathbf{w}_j)\]
dove \(c_j\) sono pesi e \(\overline{y}(x: w) \in \mathbb{R}\) sono funzioni semplici dell'input \(x\) parametrizzate da \(\mathbf{w}\).
3.2.1 Fitting Additive Models
Passando al caso caso dei modelli additivi, per addestrare questi modelli si definisce una appropriata loss function da minimizzare rispetto al training data
\[\underset{c_j, \mathbf{w}_j}{\min} \;\; \sum\limits_{i = 1}^n L\Big(t_i, \sum\limits_{k = 1}^m c_k \overline{y}(x_i; \mathbf{w}_k)\Big)\]
Tipicamente però per molte funzioni loss \(L\) e per molti predittori \(\overline{y}\) minimizzare questa funzione risulta troppo difficile. L'idea quindi è quella di apprendere questo modello in modo iterativo.
3.2.2 Forward Stagewise Additive Modeling
Il modellamento additivo viene effettuato a passi in avanti, considerando i modelli dal primo all'ultimo, e aggiungendo una basis function alla volta in modo greedy. In particolare si procede come segue:
Si imposta \(y_0(x) = 0\).
Per ogni \(k = 1,\ldots,m\):
Si calcola
\[(\hat{c}_k, \hat{\mathbf{w}}_k) = \underset{c_k, \mathbf{w}_k}{\text{argmin}} \sum\limits_{i = 1}^n L(t_i, y_{k-1}(x_i) + c_k \overline{y}(x_i;\mathbf{w}_k))\]
Si imposta
\[y_k(x) = y_{k-1}(x) + \hat{c}_k \overline{y}(x;\mathbf{w}_k)\]
In particolare quindi si apprende di volta in volta senza cambiare i termini precedentemente aggiunti.
3.2.3 Adaboost as Additive Model
Adaboost può essere interpretato come l'apprendimento di un modello additivo con funzione di loss esponenziale
\[L(y, f(x)) = e^{-tf(x)}\]
3.3 Gradient Boosting
Dato un training set \((x_i, t_i)\), \(i=1,\ldots,n\), il nostro obiettivo è quello di trovare un modello \(y(x)\) che minimizzi una certa funzione di costo, che per semplicità assumiamo essere la square loss function.
Assumiamo di avere a disposizione un modello iniziale \(y^{(1)}(x)\) con residui
\[t_i 0 y^{(1)}(x_i) = t_i - y_i^{(1)}\]
Tramite l'utilizzo di questo classificatore siamo in grado di costruire un nuovo dataset, formato dalle coppie \((x_i, t_i - y_i^{(1)})\), per \(i=1,\ldots,n\). A partire da questo dataset andiamo ad addestrare un nuovo modello \(\overline{y}^{(1)}(x)\) sempre addestrato per minimizzare la square loss.
Definiamo quindi il seguente modello
\[y_2(x) = y_1(x) + \overline{y}_1(x)\]
notiamo come \(y_2(x)\) è un modello migliore di \(y_1(x)\), in quanto il modello aggiunto \(\overline{y}_1(x)\) viene utilizzato per compensare i lati più deboli del modello \(y_1(x)\).
Se poi anche \(y_2(x)\) non è abbastanza soddisfacente, allora possiamo fare la stessa cosa addestrando un nuovo modello supplementare \(\overline{y}_2(x)\) che possiamo utilizzare per definire il modello
\[y_3(x) = y_2(x) + \overline{y}_2(x)\]
3.3.1 Link to Gradient Descent
Perché c'è la parola "gradient" nell'espressione "gradient boosting"? Come è correlata la procedura appena descritta con la gradient descent?
Consideriamo la square loss function \(L(t, y) = 1/2(t - y)^2\). Il nostro obiettivo è quello di minimizzare il rischio \(R = \sum_{i = 1}^n L(t_i, y_i)\) andando ad agire sui vari \(y_i\).
Considerando \(y_i\) come parametri del modello, calcolando le derivate otteniamo
\[\frac{\partial R}{\partial y_i} = y_i - t_i\]
I residui possono quindi essere considerati come gradienti negativi
\[t_i - y_i = - \frac{\partial R}{\partial y_i}\]
Il modello \(\overline{y}(x)\) può dunque essere derivato considerando il dataset
\[(x_i, t_i - y_i) = \Bigg(x_i, - \frac{\partial R}{\partial y_i} \Bigg), \,\,\, i=1,\ldots,n\]
3.3.2 Algorithm
L'algoritmo può quindi essere formalizzato come segue
Inizialmente settiamo il primo predittore nel seguente modo
\[y^{(1)}(x) = \frac{1}{n} \sum\limits_{i = 1}^n t_i\]
Per \(k=1,\ldots,m\):
Calcoliamo i gradienti negativi
\[-g_i^{(k)} = -\frac{\partial R}{\partial y_i} \Bigg|_{y_i = y^{(k)}(x_i)} = -\frac{\partial }{\partial y_i} L(t_i, y_i)\Bigg|_{y_i = y^{(k)}(x_i)} = t_i - y^{(k)}(x_i)\]
Successivamente si allena un weak learner \(y^{(k)}(x)\) rispetto ai gradienti negativi considerando il dataset \((x_i, -g_i^{(k)})\) per \(i=1,\ldots,n\)
A partire dal weak learner definamo il nuovo classificatore
\[y^{(k+1)}(x) = y^{(k)}(x) + \overline{y}^{(k)}(x)\]
3.3.3 Regression
Una volta che abbiamo espresso l'algoritmo tramite il gradiente possiamo applicarlo anche ad altre loss functions. Questo ci permette quindi di applicare questa tecnica del gradient boosting anche per problemi di regressione.
Dato che la square loss non è robusta ad outliers, ovvero ad elementi che sono statisticamente molto eccentrici rispetto agli altri, potrei pensare a considerare altre funzioni di loss, tra cui
Absolute loss
\[\begin{split} L(t, y) &= |t - y| \\ -g &= \text{sgn}(t - y) \\ \end{split}\]
Huber loss
\[\begin{split} L(t, y) &= \begin{cases} \frac12 (t - y)^2 & |t - y| \leq \delta \\ \delta(|t - y|) - \frac{\delta}{2} & |t - y| > \delta \\ \end{cases} \\ \\ -g &= \begin{cases} y - t & |t - y | \leq \delta \\ \delta \cdot \text{sgn}(t - y) & |t - y| > \delta \\ \end{cases} \end{split}\]
3.3.4 Classification
Lo stesso algoritmo può essere applicato anche nel caso di classificazione multiclasse con \(K\) classi diverse.
In particolare...