ML - 30 - Principal Component Analysis
Lecture Info
Date:
Lecturer: Giorgio Gambosi
Slides: (ml_15_pca-slides.pdf)
In questa lezione abbiamo trattato la principal component anaylsis, un algoritmo molto importante per quanto riguarda la dimensionality reduction di un dataset, un importante step in un processo di addestramento non supervisionato, utile anche però in un setting supervisionato più tradizionale.
1 Curse of Dimensionality
In generale avere dataset di dimensionalità (numero di features) molto elevata presenta una serie di inconvenienti, tra cui troviamo:
In situazioni del genere i dati tendono ad essere sparsi, ovvero la distanza degli elementi tra di loro tende a crescere esponenzialmente al crescere della dimensionalità. Questo può creare problemi quando utilizziamo modelli che fanno riferimenti a concetti di "località".
Il numero elevato di features tende ad aumentare notevolmente il numero di coefficienti da apprendere. Ad esempio se abbiamo uno spazio \(D\) dimensionale e un polinomio di ordine \(3\) della forma
\[y(x, \mathbf{w}) = w_0 + \sum\limits_{i = 1}^D w_i \cdot x_i + \sum\limits_{i = 1}^D \sum\limits_{j = 1}^D w_{i,j} \cdot x_i x_j + \sum\limits_{i = 1}^D\sum\limits_{j = 1}^D\sum\limits_{k = 1}^D w_{i,j,k} \cdot x_i x_j x_k\]
il numero di coefficienti da imparare è \(O(D^M)\)
Questi problemi (in particolare il primo) vanno sotto il nome della curse of dimensionality.
2 Dimensionality Reduction
Per un dato classificatore, la dimensione del training set necessario per acquisire un determinato livello di accuracy tende a crescere esponenzialmente all'aumentare delle features.
Risulta quindi importante limitare il numero delle featues andando ad identificare quelle meno discriminanti per poterle eliminare.
La riduzione di dimensionalità può essere effettuata in due modi alternativi:
Feature selection: A partire dall'insieme complessivo delle features si identifica un sottoinsieme di features che sono il più informative possibile rispetto al training set e si eliminano le restanti features. Questo può essere fatto ad esempio utilizzando la mutual information.
Feature extraction: Si identifica una proiezione del dataset su uno spazio di dimensione più piccola in modo tale che la varietà degli elementi (la varianza del dataset) è mantenuta il più possibile durante la proiezione.
La feature extraction differisce dalla feature selection in quanto nella feature selection le features finali sono esattamente quelle di partenza, mentre nel caso della extraction le features finali sono calcolate mediante una trasformazione delle features originali.
I metodi di feature extraction possono poi essere divisi ulteriormente in due gruppi a seconda del tipo di trasformazione effettuata. Tra questi troviami:
Linear projection:
Principal Component Analysis (PCA).
Probabilistic PCA.
Factor analysis.
Non-linear projection:
Manifold learning.
Autoencoders.
3 PCA
Consideriamo un insieme di dati in uno spazio bidimesionale. In generale possiamo avere due casi distinti: un caso in cui i dati sono posizionati nell'intero spazio bidimensionale, e un altro caso in cui i dati sono posizionati lungo una retta, ovvero sono allineati lungo un sottopiano di dimensione inferiore.
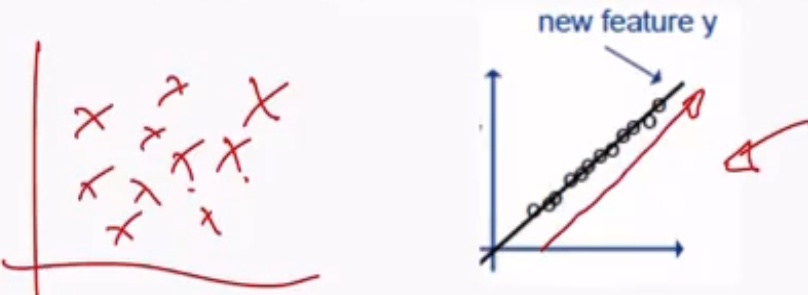
Nel secondo caso (quello a destra), se invece di rappresentare gli elementi in uno spazio bidimensionale gli proiettiamo in uno spazio unidimensionale (la retta stessa), avremmo comunque conservato la maggior parte delle informazioni del dataset.
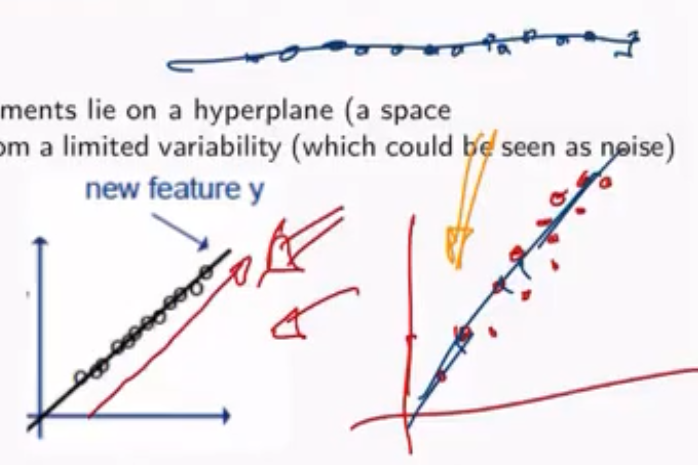
La principal component analysis procede proprio in questo modo: a partire da uno spazio di dimensione \(d\) si cerca di individuare un sottospazio di dimensione \(d^{'}\) (con \(d^{'} < d\)) in cui è possibile proiettare gli elementi dello spazio originale nel sottospazio trovato in modo da ottenere una rappresentazione sufficientemente "fedele" del dataset originario. Notiamo che più piccola è la dimensione del sottospazio e maggiore sarà l'informazione persa.
In questo caso per rappresentazione "fedele" stiamo intendendo che le distanze tra gli elementi e le loro proiezioni sono molto piccole, eventualmente minime.
3.1 Caso \(d^{'} = 0\)
Consideriamo il caso banale in cui \(d^{'}=0\), ovvero in cui vogliamo rappresentare tutto il training set, che è formato da \(n\) vettori \(d\) dimensionali \(x_1, \ldots, x_n\) tramite un solo vettore \(x_0\) nel modo più "fedele" possibile, ovvero in modo tale da minimizzare la seguente quantità
\[J(x_0) = \sum\limits_{i = 1}^n ||x_0 - x_i||^2\]
In questo caso è facile vedere che il punto migliore è dato dalla media degli \(n\) vettori. In formula,
\[x_0 = \mathbf{m} = \frac{1}{n} \sum\limits_{i = 1}^n x_i\]
Notiamo infatti che
\[\begin{split} J(x_0) &= \sum\limits_{i = 1}^n ||(x_0 - \mathbf{m}) - (x_i - \mathbf{m})||^2 \\ &= \sum\limits_{i = 1}^n ||x_0 - \mathbf{m}||^2 - 2 \sum\limits_{i = 1}^n (x_0 - \mathbf{m})^T (x_i - \mathbf{m}) + \sum\limits_{i = 1}^n ||x_i - \mathbf{m}||^2 \\ &= \sum\limits_{i = 1}^n ||x_0 - \mathbf{m}||^2 -2 (x_0 - \mathbf{m})^T \sum\limits_{i = 1}^n (x_i - \mathbf{m}) + \sum\limits_{i = 1}^n ||x_i - \mathbf{m}||^2 \\ &= \sum\limits_{i = 1}^n || x_0 - \mathbf{m}||^2 + \sum\limits_{i = 1}^n ||x_i - \mathbf{m}||^2 \\ \end{split}\]
Inoltre, dato che
\[\sum\limits_{i = 1}^n (x_i - \mathbf{m}) = \sum\limits_{i = 1}^n x_i - n \cdot \mathbf{m} = n \cdot \mathbf{m} - n \cdot \mathbf{m} = 0\]
Abbiamo che il secondo termine non dipende da \(x_0\), mentre il primo termine è uguale a \(0\) per \(x_0 = m\).
3.2 Caso \(d^{'} = 1\)
Il caso visto precedentemente è troppo approssimativo per rappresentare un intero dataset. Un caso più interessante invece è il caso in cui \(d^{'}=1\), ovvero quando utilizziamo una retta per rappresentare il nostro dataset.
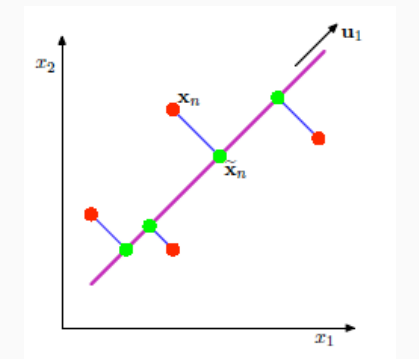
L'idea è quindi quella di considerare la retta migliore che passa per il vettore medio \(\mathbf{m}\).
Notiamo che qualunque retta che passa per il punto medio può essere rappresentata in modo vettoriale come segue
\[x = \alpha \mathbf{u}_1 + \mathbf{m}\]
dove \(\mathbf{u}_i\) è il vettore unitario \((||\mathbf{u}_1|| = 1)\) che segue la direzione della nostra retta di interesse, mentre \(\alpha\) è la distanza tra \(x\) e \(\mathbf{m}\) nella retta.
3.2.1 Best way to project
Consideriamo adesso un punto del dataset \(x_i\), e consideriamo la proiezione di questo punto nella retta \(\tilde{x}_i = \alpha_i \mathbf{u}_1 + \mathbf{m}\). Vogliamo trovare l'insieme delle proiezioni che minimizzano l'errore quadratico.
Ora, l'errore quadratico può essere scritto nel seguente modo
\[\begin{split} J(\alpha_1, \ldots, \alpha_n, \mathbf{u}_1) &= \sum\limits_{i = 1}^n || \tilde{x}_i - x_i||^2 \\ &= \sum\limits_{i = 1}^n || (\mathbf{m} - \alpha_i \mathbf{u}_1) - x_i||^2 \\ &= \sum\limits_{i = 1}^n || \alpha_i \mathbf{u}_1 - (x_i - \mathbf{m})||^2 \\ &= \sum\limits_{i = 1}^n \alpha_i^2 ||\mathbf{u}_1||^2 + \sum\limits_{i = 1}^n ||x_i - \mathbf{m}||^2 - 2 \sum\limits_{i = 1}^n \alpha_i \mathbf{u}_1^T (x_i - \mathbf{m}) \\ &= \sum\limits_{i = 1}^n \alpha_i^2 + \sum\limits_{i = 1}^n ||x_i - \mathbf{m}||^2 - 2 \sum\limits_{i = 1}^n \alpha_i \mathbf{u}_i^T (x_i - \mathbf{m}) \\ \end{split}\]
andandoci a calcolare le derivate rispetto ai valori \(\alpha_k\) è data da
\[\frac{\partial }{\partial \alpha_k} J(\alpha_1, \ldots, \alpha_n, \mathbf{u}_1) = 2 \alpha_k - 2 \mathbf{u}_1^T (x_k - \mathbf{m})\]
che è \(0\) proprio quando \(\alpha_k = \mathbf{u}_1^T (x_k - \mathbf{m})\), che è la proiezione ortogonale di \(x_k\) nella retta.
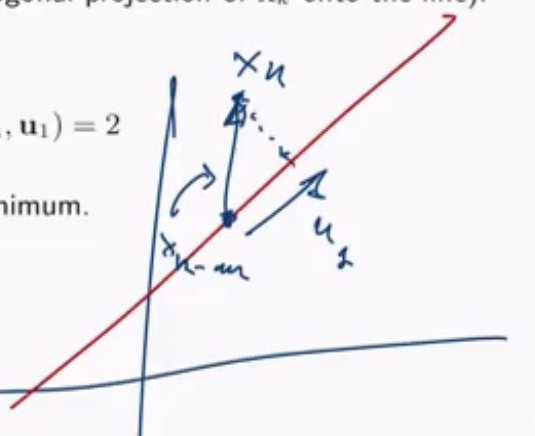
Se poi ci andiamo a calcolare la derivata seconda otteniamo
\[\frac{\partial }{\partial \alpha_k^2} J(\alpha_1, \ldots, \alpha_n, \mathbf{u}_1) = 2\]
e quindi il punto trovato è proprio un punto di minimo.
Da questo segue che il modo migliore di proiettare i vari punti lungo una retta è tramite la proiezione ortogonale dei vari vettori. Così facendo siamo in grado di minimizzare la somma degli errori quadratici.
3.2.2 Best direction
Consideriamo adesso il problema di capire qual è la migliore retta, ovvero qual è la migliore direzione \(\mathbf{u}_1\) della retta. A tale fine consideriamo la matrice \(d \times d\) di covarianza del dataset
\[\mathbf{S} = \frac{1}{n} \sum\limits_{i = 1}^n (x_i - \mathbf{m})(x_i - \mathbf{m})^T\]
Andando ad inserire nell'espressione della funzione di costo quadratico i valori di \(\alpha_k\) che minimizzano l'errore, otteniamo la seguente espressione
\[\begin{split} J(\mathbf{u}_1) &= \sum\limits_{i = 1}^n \alpha_i^2 + \sum\limits_{i = 1}^n ||x_i - \mathbf{m}||^2 - 2 \sum\limits_{i = 1}^n \alpha_i \mathbf{u}_i^T (x_i - \mathbf{m}) \\ &= -\sum\limits_{i = 1}^n \Big(\mathbf{u}_1^T (x_i - \mathbf{m}) \Big)^2 + \sum\limits_{i = 1}^n ||x_i - \mathbf{m}||^2 \\ &= -\sum\limits_{i = 1}^n \mathbf{u}_1^T (x_i - \mathbf{m})(x_i - \mathbf{m})^T \mathbf{u}_1 + -\sum\limits_{i = 1}^n ||x_i - \mathbf{m}||^2 \\ &= -n \cdot \mathbf{u}_1^T \mathbf{S} \mathbf{u}_1 + \sum\limits_{i = 1}^n ||x_i - \mathbf{m}||^2 \\ \end{split}\]
A questo punto facciamo qualche considerazione generale:
Il vettore
\[\mathbf{u_1}^T (x_i - \mathbf{m})\]
è la proiezione di \(x_i\) rispetto alla retta.
Il prodotto
\[\mathbf{u}_1^T (x_i - \mathbf{m})(x_i - \mathbf{m})^T \mathbf{u}_1\]
è la varianza della proiezione d \(x_i\) rispetto al vettore medio \(\mathbf{m}\).
La somma
\[\sum\limits_{i = 1}^n \mathbf{u}_1^T (x_i - \mathbf{m})(x_i - \mathbf{m})^T \mathbf{u}_1 = n \cdot \mathbf{u}_1^T \mathbf{S} \mathbf{u}_1\]
è la varianza complessiva delle proiezioni dei vettori \(x_i\) rispetto al vettore media \(\mathbf{m}\).
Quindi minimizzare \(J(\mathbf{u}_1)\) è equivalente a massimizzare \(\mathbf{u}_1^T \mathbf{S} \mathbf{u}_1\). Detto in altre parole, \(J(\mathbf{u}_1)\) è minimo se \(\mathbf{u}_1\) rappresenta la direzione che mantiene la massima varianza nel dataset. Il nostro problema diventa quindi il seguente
\[\begin{split} &\underset{\mathbf{u}_1}{\max} \,\,\, &\mathbf{u}_1^T \mathbf{S} \mathbf{u}_1 \\ &\text{where } \\ & \, &||\mathbf{u}_1|| =1 \,\,\,\,\, \end{split}\]
Utilizzando i moltiplicatori di Lagrange otteniamo il seguente problema di ottimizzazione senza vincoli
\[u = \mathbf{u}_1^T \mathbf{S} \mathbf{u}_1 - \lambda_1(\mathbf{u}_1^T \mathbf{u}_1 - 1)\]
per risolvere questo problema calcoliamo la derivata rispetto a \(\mathbf{u}_1\)
\[\frac{\partial u}{\partial \mathbf{u}_1} = 2 \mathbf{S} \mathbf{u}_1 - 2 \lambda_1 \mathbf{u}_1\]
settandola a \(0\) troviamo
\[\mathbf{S} \mathbf{u}_1 = \lambda_1 \mathbf{u}_1\]
Da questo possiamo notare che \(u\) è massimizzato se \(\mathbf{u}_1\) è un autovettore di \(\mathbf{S}\). In questo caso la varianza complessiva corrisponde al valore del rispettivo autovalore
\[\mathbf{u}_1^T \mathbf{S} \mathbf{u}_1 = \mathbf{u}_1^T \lambda_1 \mathbf{u}_1 = \lambda_1 \mathbf{u}_1^T \mathbf{u}_1 = \lambda_1\]
La varianza delle proiezioni totale è massimizza (e l'errore minimizzato) se \(\mathbf{u}_1\) è l'autovettore di \(\mathbf{S}\) corrispondente al massimo autovalore \(\lambda_1\).
3.3 Caso \(d^{'} > 1\)
Nel caso in cui vogliamo proiettare in uno spazio \(d^{'} > 1\) è possibile dimostrare che l'impostazione da seguire è analoga a quella mostrata nei casi precedenti.
In particolare l'errore quadrato è sempre minimizzato andando a proiettare i punti del dataset nel sottospazio di dimensione \(d^{'}\) definito dai \(d^{'}\) autovettori che corrispondono ai \(d^{'}\) autovalori più grandi di \(\mathbf{S}\).
Se poi assumiamo che i dati possono essere modellati da una distribuzione gaussiana \(d\) dimensionale con media \(\mathbf{\mu}\) e matrice di covarianz \(\mathbf{\Sigma}\), allora PCA ritorna un sottospazio \(d^{'}\) dimensionale che corrisponde all'iperpiano ottenuto dagli autovattori associati agli \(d^{'}\) autovalori più grandi della matrice \(\mathbf{\Sigma}\).
3.4 Example
Consideriamo la rappresentazione di una cifra su una griglia \(D = 28 \times 28\), ovvero rappresentiamo una cifra con un vettore in uno spazio a \(784\) dimensioni. Applicando PCA per vari valori di \(M=d^{'}\) otteniamo la seguente situazione
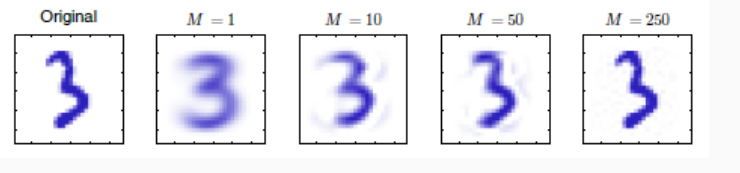
Come è possibile vedere dai seguenti esempi, la PCA elimina la minima informazione dal dataset. Più piccolo è \(d^{'}\) rispetto alla dimensione dello spazio originale e più informazione viene persa.
3.5 Choosing \(d^{'}\)
Per capire il valore di \(d^{'}\) l'idea è quella di considerare gli autovalori della matrice di covarianza del dataset.
Tipicamente se si va a vedere il grafico dei valori degli autovalori di una matrice ordinati in modo non-decrescente si ottiene una figura del genere
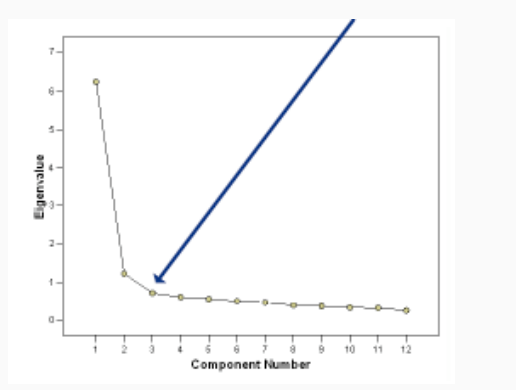
L'idea quindi è quella di capire quanti autovalori prendere, partendo dal più grande e continuando fino a quando le differenze tra un autovalore e il successivo diventa sufficientemente piccola.
Consideriamo in particolare per ogni \(k < d\) il valore
\[r_k = \frac{\sum\limits_{i = 1}^k \lambda_i^2}{\sum\limits_{i = 1}^n \lambda_i^2}\]
Quando \(r_1 < \ldots < r_d\) sono noti, un certa quantità di varianza \(p\) può essere mantenuta andando a settare
\[d^{'} = \underset{r \in \{1, \ldots, d\}}{\text{argmin}} r_i > p\]