ML - 31 - Singular Value Decomposition
Lecture Info
Date:
Lecturer: Giorgio Gambosi
Slides: (ml_15_pca-slides.pdf)
In questa lezione abbiamo tratto un ulteriore modo per effettuare dimensionality reduction tramite la Singular Value Decomposition (SVD), andando a trattare un caso particolare in cui questa tecnica può essere applicata.
1 SVD
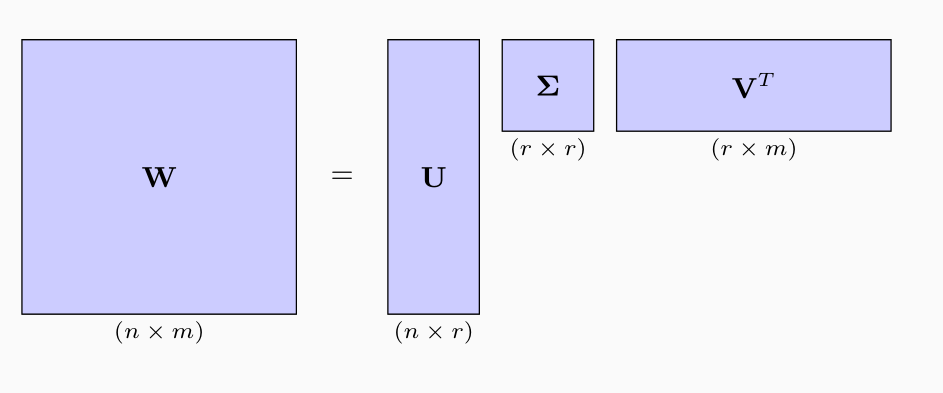
Sia \(\mathbf{W} \in \mathbb{R}^{n \times m}\) una matrice di rango \(r \leq \min{(n, m)}\), e sia \(n > m\). Allora esistono le seguenti matrici
\(\mathbf{U} \in \mathbb{R}^{n \times r}\) ortonormale (ovvero \(\mathbf{U}^T \mathbf{U} = \mathbf{I}_r\))
\(\mathbf{V} \in \mathbb{R}^{m \times r}\) ortonormale (ovvero \(\mathbf{V}^T \mathbf{V} = \mathbf{I}_r\))
\(\mathbf{\Sigma} \in \mathbb{R}^{r \times r}\) diagonale.
tali che
\[\mathbf{W} = \mathbf{U} \mathbf{\Sigma} \mathbf{V}^T\]
Questa decomposizione prende il nome di singular value decomposion. Graficamente otteniamo,
1.1 Why it Exists?
Consideriamo adesso la matrice \(\mathbf{A} = \mathbf{W}^T \mathbf{W} \in \mathbb{R}^{m \times m}\). È possibile dimostrare le seguenti cose:
\(A\) è simmetrica.
\(A\) è semidefinita positiva.
Tutti gli autovalori di \(A\) sono reali.
Gli autovettori di \(A\) che corrispondono ad autovalori diversi sono ortonormali tra loro.
Deve esistere un insieme di autovettori di \(A\) che formano una base ortonormale.
Tutti gli autovettori di\(A\) sono maggiori di \(0\).
Complessivamente abbiamo che \(\mathbf{A} = \mathbf{W}^T \mathbf{W} \in \mathbb{R}^{m \times m}\) ha \(r\) reali e positivi autovalori \(\lambda_1, \ldots, \lambda_r\), con i corrispondenti autovettori \(v_1, \ldots, v_r\) ortonormali tra loro con
\[\mathbf{A} v_i = (\mathbf{W}^T \mathbf{W}) v_i = \lambda_i v_i\]
Se definiamo adesso gli \(r\) valori singolari come le radici degli autovalori
\[\sigma_i = \sqrt{\lambda_i} \;\;\;\;,\;\;\; i = 1,\ldots,r\]
e consideriamo il seguente insieme di vettori
\[\mathbf{u}_i = \frac{1}{\sigma_i} \mathbf{W} v_i \;\;\;\;,\;\;\; i = 1,\ldots,r\]
È possibile osservare che
\(u_1, \ldots, u_r\) sono ortogornali.
\(u_1, \ldots, u_r\) hanno norma unitaria.
A questo punto possiamo considerare le tre matrici seguenti
La matrice \(\mathbf{V} \in \mathbb{R}^{m \times r}\) che ha i vettori \(v_1, \ldots, v_r\) come colonne
La matrice \(\mathbf{U} \in \mathbb{R}^{n \times r}\) che ha i vettori \(u_1, \ldots, u_r\) come colonne
La matrice \(\mathbf{\Sigma} \in \mathbb{R}^{r \times r}\) che è una matrice diagonale avente i valori singolari sulla diagonale.
A questo punto è possibile osservare che
\[\mathbf{W} \mathbf{V} = \mathbf{U} \mathbf{\Sigma}\]
e quindi, dato che \(\mathbf{V}\) è ortogonale, ovvero \(\mathbf{V}^{-1} = \mathbf{V}^T\), otteniamo che
\[\mathbf{W} = \mathbf{U} \mathbf{\Sigma} \mathbf{V}^-1 = \mathbf{U} \mathbf{\Sigma} \mathbf{V}^T\]
2 PCA and SVD
Dal punto di vista computazionale la SVD viene implementata in tutte le librerie che comprendono funzionalità di algebra lineare. È possibile poi mostrare che per eseguire una PCA su \(\mathbf{X}\) è sufficiente calcolata la SVD della deguente matrice
\[\tilde{\mathbf{X}} = \mathbf{X} \Big(\mathbf{I} - \frac{1}{n} \mathbf{1} \mathbf{1}^T\Big) = \mathbf{U} \mathbf{\Sigma} \mathbf{V}^T\]
Le componenti principali di \(\mathbf{X}\) sono le colonne di \(\mathbf{V}\) con i corrispondenti autovalori dati dagli elementi della diagonale di \(\mathbf{\Sigma}^2\).
3 Co-occurence data
I dati di co-occorrenza sono dati strutturati come coppie i cui elementi vengono presi da cue collezioni \(\mathbf{V}, \mathbf{D}\).
I nostri dati sono quindi una sequenza di osservazioni
\[\mathbf{W} = \{(w_1, d_1), \ldots, (w_N, d_N)\}\]
con \(w_i \in \mathbf{V}\) e \(d_i \in \mathbf{D}\). Una tipica interpretazione di queste coppie è quella delle occorrenze dei termini nei documenti.
Un possibile modo per rappresentare questo tipo di dati è tramite una matrice.
Osserviamo come tipicamente questa matrice, anceh se è molto grande, risulta anche essere molto sparsa, ovvero che contiene molti elementi nulli.
4 Latent Semantic Analysis
L'idea della LSA è quella di rappresentare la matrice fatta vedere prima tramite la SVD. Questa decomposizione ci permette di avere una rappresentazione ridotta in termine di dimensionalità degli elementi in gioco.
4.1 Assumption
L'approccio LSA (Latent Semantic Analysis) si basa su tre ipotesi:
La matrice \(\mathbf{V}, \mathbf{D}\) contiene dei dati da cui possono essere estratte delle informazioni semanticamente significative.
Per derivare queste informazioni siamo interessati ad effettuare della dimensionality reduction.
"termini" e "documenti" possono essere modellati tramite punti (vettori) in uno spazio euclideo.
4.2 Model
Gli elementi a nostra dispozione sono i seguenti:
Un dizionario \(\mathbf{V}\) di \(V = |\mathbf{V}|\) termini \(t_1, \ldots, t_V\).
Un corpus \(\mathbf{D}\) di \(D = | \mathbf{D}|\) documenti \(d_1, \ldots, d_D\).
Ogni documento \(d_i\) è una sequenza di \(N_i\) occorrenze di termini da \(\mathbf{V}\).
L'idea è quella di considerare ogni documento \(d_i\) come un multiset di \(N_i\) termini di \(\mathbf{V}\) (questa ipotesi è detta bag of words).
Abbiamo poi una corrispondenza tra \(\mathbf{V}\), \(\mathbf{D}\) e uno spazio vettoriale \(\mathcal{S}\). Ad ogni termine \(t_i\) associamo un vettore \(u_i\) e ad ogni documento \(d_j\) associato un vettore \(v_j \in \mathcal{S}\).
Per rappresentare la relazione tra termini e documenti utilizziamo una occurence matrix (matrice di occorrenza) \(\mathbf{W} \in \mathbb{R}^{V \times D}\), dove \(\mathbf{W}(i, j)\) contiene l'occorrenza del termine \(t_i\) nel documento \(d_j\), e tale valore è ottenuto tramite delle funzioni predefinite (tipicamente tf-idf, o entropy related).
4.3 Problems
Il modello appena descritto presenta vari problemi, tra cui troviamo:
I valori di \(V\) e \(D\) tipicamente sono molto grandi.
I vettori per \(t_i\) e \(d_j\) sono molto sparsi.
Gli spazi vettoriali per termini e documenti sono diversi.
4.4 Solution (SVD)
Per risolvere questi problemi si applica una SVD alla matrice delle occorrenze \(\mathbf{W} \in \mathbb{R}^{n \times m}\).
La SVD infatti ci dice che dato il rango \(d \leq \min{(n, m)}\) con \(n > m\), allora esiste una decomposizione della forma
\[\mathbf{W} = \mathbf{U} \mathbf{\Sigma} \mathbf{V}^T\]
con,
\(\mathbf{U} \in \mathbb{R}^{n \times d}\) ortonormale.
\(\mathbf{V} \in \mathbb{R}^{m \times d}\) ortonormale.
\(\mathbf{Z} \in \mathbb{R}^{d \times d}\) diagonale.
Graficamente,
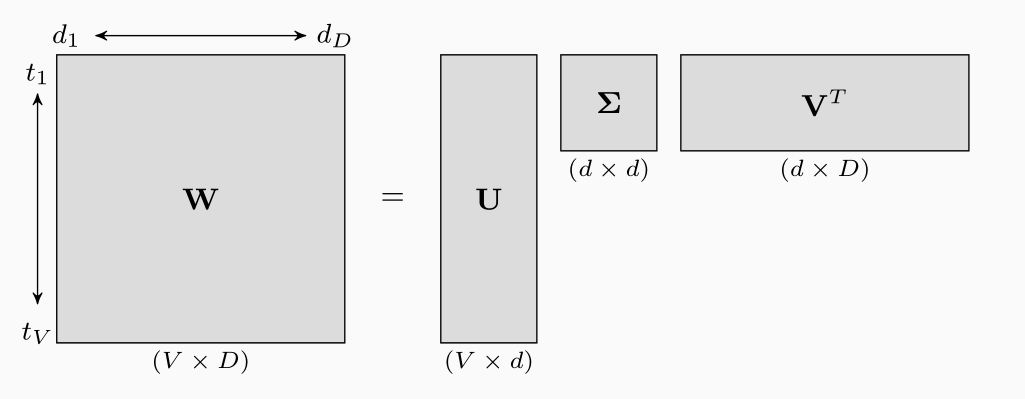
Andando ad interpretare le righe di \(\mathbf{W}\) come termini e le colonne di \(\mathbf{W}\) come documenti otteniamo che tramite la SVD siamo in grado di rappresentare sia i termini che i documenti in un sottospazio vettoriale di dimensione minore.
Anche se tecnicamente non conosciamo il valore di \(d\), l'idea è quello di fissarlo in modo arbitrario. Così facendo otteniamo una matrice approssimata
\[\mathbf{W} \approx \overline{\mathbf{W}} = \mathbf{U} \mathbf{\Sigma} \mathbf{V}^T\]
Notiamo però che vale la seguente proprietà
\[\underset{A: \text{rank}(A) =d}{\min} || \mathbf{A}||_2 = || \mathbf{W} - \overline{\mathbf{W}} ||_2\]
e quindi la matrice \(\overline{\mathbf{W}}\) è la migliore approssimazione possibile di \(\mathbf{W}\) rispetto a tutte le matrici di rango \(d\) secondo la norma di Frobenius
\[||\mathbf{A}||_2 = \sqrt{\sum\limits_{i = 1}^m \sum\limits_{j = 1}^n | a_{i,j} | ^2}\]
4.5 Interpretation
La SVD definisce quindi una trasformazione tra due spazi vettoriali \(\mathcal{V} \in \mathbb{Z}^D\) e \(\mathcal{D} \in \mathbb{Z}^V\) in uno spazio vettoriale continuo della stessa dimensione \(\mathcal{T} \in \mathbb{R}^d\).
La dimensione di \(\mathcal{T}\) è minore o uguale al rank (sconosciuto) della matrice di occorrenza \(\mathbf{W}\), ed è legata alla quantità di distorsione accettabile nella proiezione.
L'idea è che \(\tilde{\mathbf{W}}\) cattura la maggior parte delle associazioni tra termini e documenti in \(\mathbf{W}\), andando a non considerare le relazioni meno significative. In particolare:
Ogni termine viene rappresentato come una combinazione lineare di concetti invisibili, che corrispondono alle colonne di \(\mathbf{V}\).
Ogni documento viene rappresentato come una combinazione lineare di topics invisibibli, corrispondendti alle colonne di \(\mathbf{U}\).