ML - 32 - Clustering I
Lecture Info
Date:
Lecturer: Giorgio Gambosi
Slides: (ml_16_clustering-slides.pdf)
In questa lezione abbiamo introdotto il problema del clustering, uno dei più importanti problemi in un contesto di apprendimento non supervisionato. Abbiamo discusso le due versioni del clusterting (partitional vs hierarchical) e abbiamo discusso due algoritmi per risolvere le due varianti: il k-means e il clusterting per aggregazione.
1 Clustering
Il problema del clusterting può essere definito come segue: consideriamo un dataset di elementi \(\mathbf{X} = (x_1, \ldots, x_n)\) con \(x_i \in \mathbb{R}^d\). Notiamo che, dato che ci troviamo in un contesto non supervisionato, non abbiamo più i target \(t_i\) per ogni \(x_i\). Quello che vogliamo fare è derivare un insieme di clusters, ovvero vogliamo partizionare \(\mathbf{X}\) in un certo numero di sottoinsiemi che contengono elementi "simili" o "vicini" tra loro.
Questi clusters sono rappresentati dai loro prototipi (prototypes) \((\mathbf{m}_1, \ldots, \mathbf{m}_k)\) con \(\mathbf{m}_j \in \mathbb{R}^d\) per \(j=1,\ldots,k\). Notiamo che non sempre i prototipi devono corrispondere ad elementi del dataset.
La soluzione di un problema di clustering ci deve fornire due cose:
I protipi dei clusters \((\mathbf{m}_1, \ldots, \mathbf{m}_k)\)
L'assegnazione degli elementi ai vari clusters, ovvero per ogni elemento \(x_i\) abbiamo \(k\) binary flags \(r_{i,j} \in \{0,1\}\) in modo tale che se \(x_i\) è assegnato al claster \(t\) allora
\[r_{i,t} = 1 \;\;\;\; r_{i, j} = 0 \,\, j \neq t\]
1.1 Types
Tecnicamente abbiamo due tipologie di problemi di clustering, che sono:
Partitional clustering: questo è il caso descritto in precedenza, in cui abbiamo un insieme di punti \(\mathbf{X} = \{x_1, \ldots, x_n\}\) e vogliamo partizionare \(\mathbf{X}\) andando ad assegnare ogni elemento di tale insieme ad uno di \(k\) clusters \(C_1, \ldots, C_k\) andando a massimizzare (o minimizzare) un dato costo \(J\). Il numero \(k\) di clusters potrebbe essere dato oppure in forme più sofisticate di clustering potrebbe dover essere calcolato.
Hierarchical clustering: Dato un insieme di punto \(\mathbf{X} = \{x_1, \ldots, x_n\}\), l'idea è quella di derivare un insieme di partizioni nidificate di \(\mathbf{X}\), che parte dalla partizione composta da tutti singletons (un cluster per elemento), alla partizione che contiene un solo elemento (l'insieme totale).
2 Partitional Clustering
Andiamo adesso ad affrontare il clustering partizionale.
2.1 Brute Force
Una prima idea potrebbe essere quella di procedere per forza bruta, andando ad elencare tutte le possibili partizioni di un insieme di \(n\) elementi in \(k\) sottoinsiemi, e andando poi a selezionare quella che minimizza \(J\).
Notiamo che il numero di tali partizioni \(P(n, k)\) può essere definito ricorsivamente come segue
\[\begin{split} P(n+1, k) &= P(n, k-1) + k \cdot P(n, k) \\ P(n, 1) &= 1 \\ P(n, n) &= 1 \\ \end{split}\]
È possibile dimostrare che tale relazione di ricorrenza può essere espressa nella seguente forma chiusa
\[P(n, k) = \frac{1}{k!} \sum\limits_{j = 0}^k (-1)^{k - j} \binom{k}{j} j^n\]
Questo numero prende il nome di stirling number del secondo tipo, che è noto essere almeno
\[\frac12 (k^2 + k + 2)k^{n - k - 1} - 1\]
per \(n \geq 2\) e \(1 \leq k \leq n - 1\). È possibile vedere che questo è un numero esponenziale, e quindi il metodo della forza bruta non è scalabile e deve essere scartato.
2.2 Clustering Cost (Sum of Squares)
Prima di andare a vedere dei metodi intelligenti per ottenere il nostro clustering, andiamo a definire il costo \(J\) di un clustering tramite la sum of squares, definita come segue
\[J(R, M) = \sum\limits_{i = 1}^k \sum\limits_{j = 1}^n r_{i,j} || x_j - \mathbf{m}_i ||^2 = \sum\limits_{i = 1}^k \sum\limits_{j = 1}^n r_{i,j} (x_j - \mathbf{m}_i)^T (x_j - \mathbf{m}_i)\]
dove \(R_{i, j} = r_{i,j}\) e \(M_i = \mathbf{m}_i\).
Notiamo quindi come questo costo viene calcolato come la somma dei quadrati delle distanze di ogni punto rispetto al prototipo del cluster a cui il punto è assegnato.
2.3 K-Means
A partire dalla funzione di costo appena data, è possibile introdurre un algoritmo semplice per effettuare il clustering che prende il nome di k-means. Consideriamo quindi il nostro dataset \(\mathbf{X} = (x_1, \ldots, x_n)\), con \(x_i \in \mathbb{R}^d\).
2.3.1 Algorithm
L'idea è quindi quella di derivare i valori \(r_{i,j}\) e \(\mathbf{m}_j\) in modo da minimizzare \(J(R, M)\) dove \(J\) è definita come la sum of squares.
L'algoritmo k-means funziona alternando due passi:
Nel primo passo assumiamo di aver definto un insieme di prototipi \(\mathbf{m}_i\). A partire da questa conoscenza andiamo a definire i valori \(r_{i,j}\) (e quindi assegnamo gli elementi ai clusters) in modo tale da minimizzare la funzione di costo
\[\sum\limits_{j = 1}^k r_{i,j} || x_i - \mathbf{m}_j||^2\]
Notiamo che il minimo è ottenuto ponendo \(r_{i,k} = 1\) (e di conseguenza \(r_{i,j} = 0\) per \(j \neq k\)) dove \(||x_i - \mathbf{m}_k||^2\) è la distanza minima. In altre parole, ogni punto è assegnato al cluster associato al prototipo più vicino al punto.
Nella seconda fase la situazione è invertita, e partendo dalla conoscenza degli \(r_{i,j}\) andiamo a minimizzare il costo rispetto a \(\mathbf{m}_i\), ovvero definiamo dei nuovi prototipi per i vari clusters. In particolare per ogni \(\mathbb{m}_k\) consideriamo
\[J = \sum\limits_{i = 1}^n \sum\limits_{j = 1}^k r_{i,j} ||x_i - \mathbf{m}_j||^2\]
che è una funzione quadratica rispetto a \(\mathbf{m}_k\). Andando a calcolare la sua derivata e settandola a \(0\), i valori di \(\mathbf{m}_k\) che forniscono il minimo sono ottenuti come segue
\[\frac{\partial J}{\partial \mathbf{m}_k} = 2 \sum\limits_{i = 1}^n r_{i,k}(x_i - \mathbf{m}_k) = 0 \implies \mathbf{m}_k = \frac{\sum_{i = 1}^n r_{i,k} \cdot x_i}{\sum_{i = 1}^n r_{i,k}}\]
L'algoritmo k-means itera tra queste fasi. Notiamo però che la funzione di costo \(J\) non aumenta mai di valore. Ad un certo punto quindi abbiamo una convergenza ad un minimo locale.
2.3.2 Example
Un esempio dell'applicazione di k-means è mostrata nel seguente esempio, in cui assumiamo che \(k=4\).
L'algoritmo inizio con la prima fase, dove inizialmente le rappresentazioni sono inizializzate in modo arbitrario (i quadrati nella figura a destra)
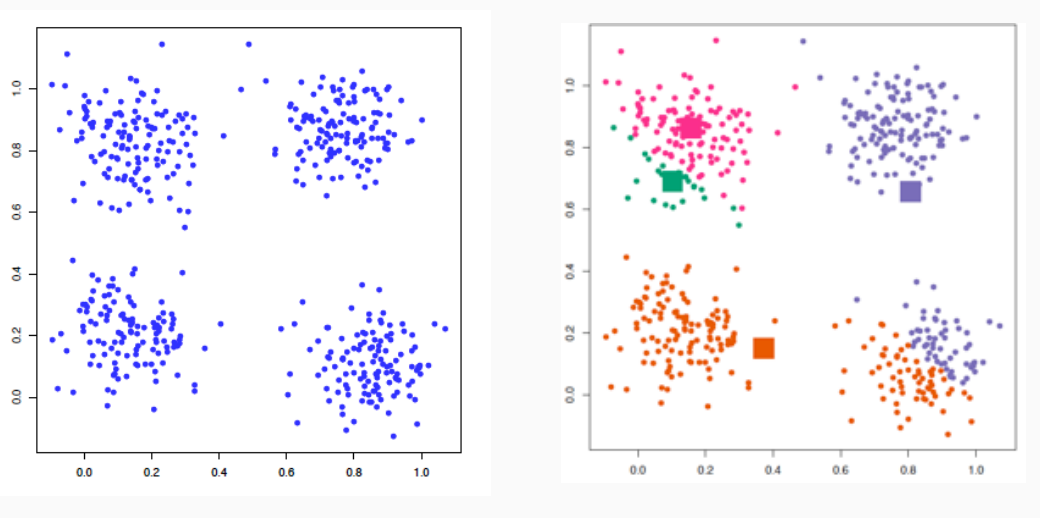
Continuando, andiamo a calcolare i nuovi baricentri dei vari insiemi
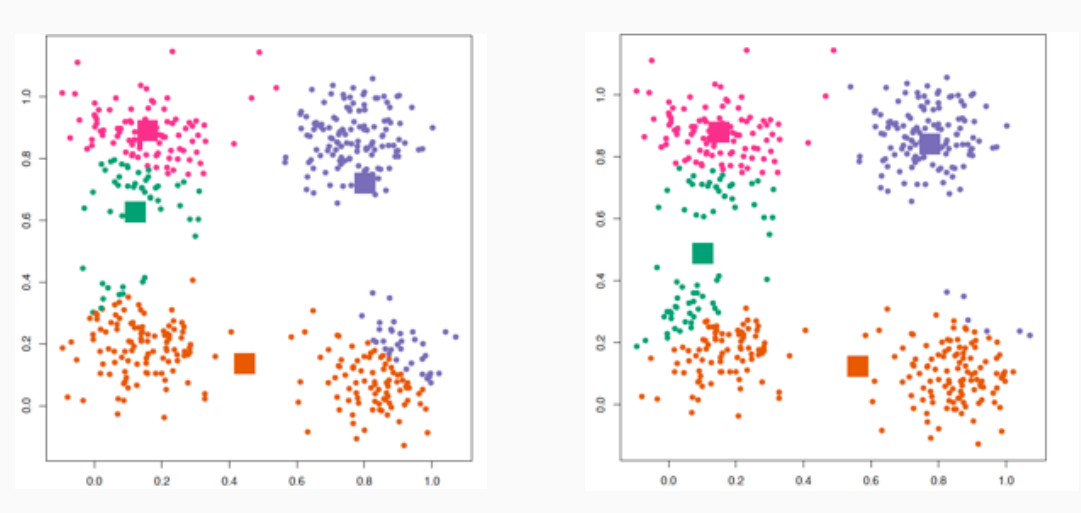
Alla fine otteniamo
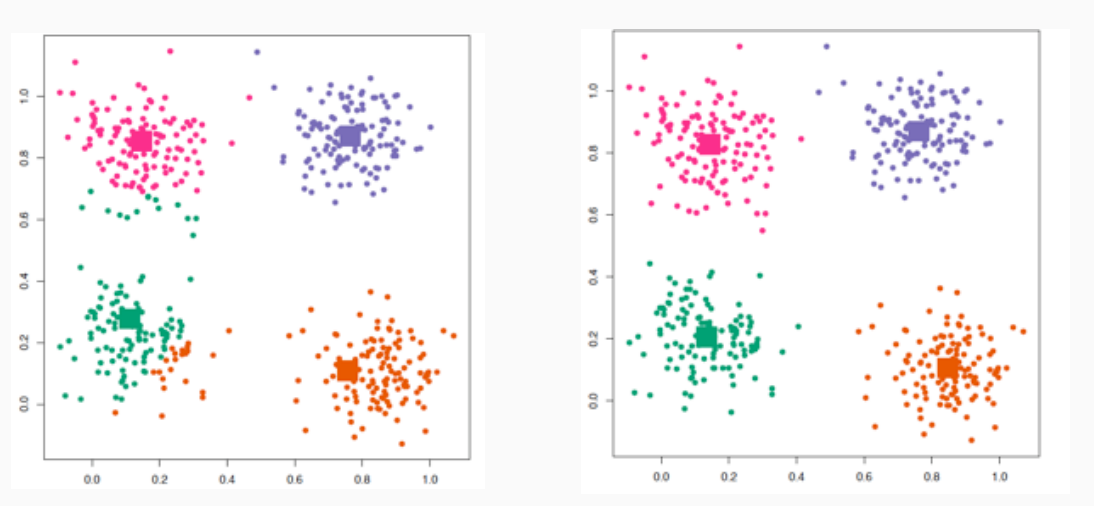
Vedendo il costo della funzione \(J\) otteniamo
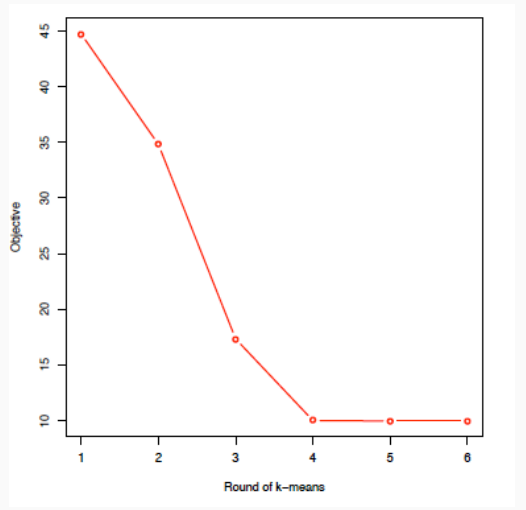
2.3.3 How to Choose \(K\)
Dato che il K-means funziona basandosi su un valore di \(K\) a questo punto uno si chiede: come si sceglie \(K\)? Notiamo infatti che cambiando il valore di \(K\) il risultato finale può cambiare molto.
La scelta di \(K\) infatti è un arogmento delicato, ed è una azione che tipicamente viene effettuata nel processo di model selection. Un possibile approccio a scegliere il giusto valore di \(K\) è tramite l'applicazione della cross-validation al variare di \(K\), misurando così facendo la qualità del clustering ottenuto.
Notiamo che la qualità del clustering ottenuto tende inevitabilmente a migliorare andando ad aumentare \(K\). In altre parole la funzione di costo è decrescente all'aumentare di \(K\). La scelta del miglior valore di \(K\) quindi non deve essere effettuata cercando esattamente il minimo, ma fermandosi non appena l'incremento di \(K\) decrementa il costo di una quantità sufficientemente limitata
Altrimenti è possibile utilizzare dei penatly terms standard rispetto al numero dei parametri. Tra questi troviamo
Akaike Information Criterion (AIC):
\[\text{AIC} = 2K -2\ln{L}\]
Bayesian Information Criterion (BIC):
\[\text{BIC} = K\ln{n} - 2\ln{L}\]
dove \(L\) è la likelihood del modello.
3 Hierarchical Clusterting
Nel caso del clustering gerarchico vogliamo ottenere un albero binario in cui i nodi rappresentano i clusters e gli archi le inclusioni tra clusters.
Dato un nodo di un cluster gerarchico, i suoi nodi rappresentano una partizione degli elementi contenuti nel cluster.
Tipicamente un algoritmo che ci calcola un clustering gerarchico può operare in due modi diversi:
Aggregation: Parte dagli \(n\) singleton clusters (le foglie) e arriva fino alla radice.
Separation: Parte dalla radice e arriva fino alle foglie.
Notiamo che per effettuare un clustering gerarchico, in particolare se si vuole procedere per aggregazione, è necessario avere a disposizione una funzione di similarità tra cluster, ovvero una funzione che dati due cluster ci da una stima di quanto questi cluster sono simili tra loro.
3.1 By Aggregation
L'algoritmo per aggregazione funziona nel seguente modo
Si inizia definendo \(n\) clusters (singleton)
Si ripete il seguente ciclo fino a quando non è rimasto un solo cluster
Si calcola una matrice delle distanze tra clusters
Si effettua il merge tra coppie di clusters che sono le più "vicine".
Le proprietà dell'albero binario ottenuto applicando questo algoritmo sono le seguenti:
Ogni prefisso dell'albero (ogni parte iniziale dell'albero) forma una partizione di elementi.
L'algoritmo fornisce un ordinamento parziale di clusterings.
3.2 Dendogram
La struttura ad albero ritornata dall'algoritmo di clustering può essere rappresentata in modo leggermente più ricco da una struttura chiamata dendogramma, che è l'albero binario rappresentato graficamente in modo tale che l'altezza dei nodi è inversamente proporzionale alla similarità dei clusters che sono accoppiati.
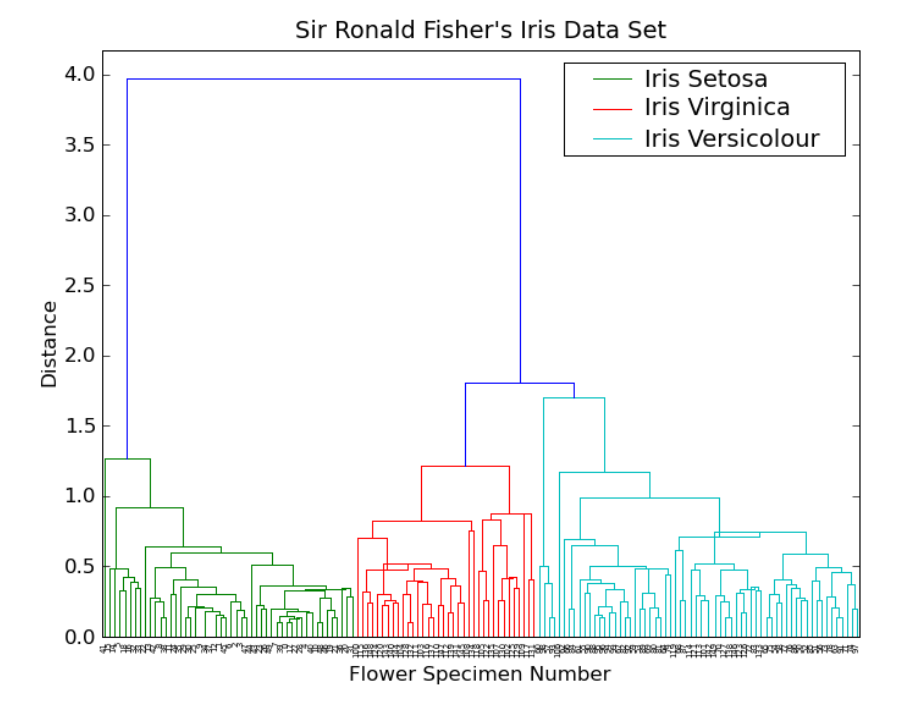
3.3 Cluster Similarity
Come abbiamo detto, il clustering gerarchico è basato sul concetto di similarità tra cluster. Esistono molti modi per definire una misura del genere. Tra questi troviamo:
Single linkage: basata sulla distanza tra i nodi più vicini
\[d_{\text{SL}}(C_1, C_2) = \underset{x_1 \in C_1, x_2 \in C_2}{\min} d(x_i, x_j)\]
Complete linkage: basata sulla distanza tra i nodi più lontani
\[d_{\text{CL}}(C_1, C_2) = \underset{x_1 \in C_1, x_2 \in C_2}{\max} d(x_i, x_j)\]
Group average:
\[d_{\text{GA}}(C_1, C_2) = \frac{1}{|C_1| \cdot |C_2|} \sum\limits_{x_1 \in C_1} \sum\limits_{x_2 \in C_2} d(x_i, x_j)\]
Notiamo che in ogni caso dobbiamo assumere di avere a disposizione una misura di distanza tra i nodi. Diverse misure di similarità tra cluster potrebbero ortare a diversi dendogrammi.