ML - 33 - Clustering II
Lecture Info
Date:
Lecturer: Giorgio Gambosi
Slides: (ml_16_clustering-slides.pdf)
In questa lezione abbiamo introdotto il concetto di mistura di distribuzione, che possiamo utilizzare per trattare il problema del clustering in modo probabilistico.
1 Mixtures of distributions
Un approccio probabilistico interessante per il problema del clustering è basato sul concetto di mistura di distribuzioni (mixtures of distributions).
Una misura additiva di distribuzioni è rappresentata da un un tipo di distribuzione \(q(x|\theta)\) un da una combinazione lineare di un insieme di istanze di questo particolare tipo di distribuzione che differiscono tra loro per il valore dei parametri. In formula,
\[p(x|\pi, \theta) = \sum\limits_{k = 1}^K \pi_k \cdot q(x | \theta_k)\]
dove,
\[\pi = (\pi_1, \ldots, \pi_K) \;\;\;\;,\;\;\;\; \theta = (\theta_1, \ldots, \theta_K)\]
Per quanto riguarda i coefficienti \(\pi_1, \ldots, \pi_k\) si assumono essere \(0 \leq \pi_k \leq 1\) e a somma \(1\)
\[\sum\limits_{k = 1}^K \pi_k = 1\]
In particolare quindi hanno le stesse proprietà di valori di probabilità di una data distribuzione discreta.
1.1 Example
Consideriamo la seguente immagine, in cui la curva blu è ottenuta come una mistura additiva delle altre curve.
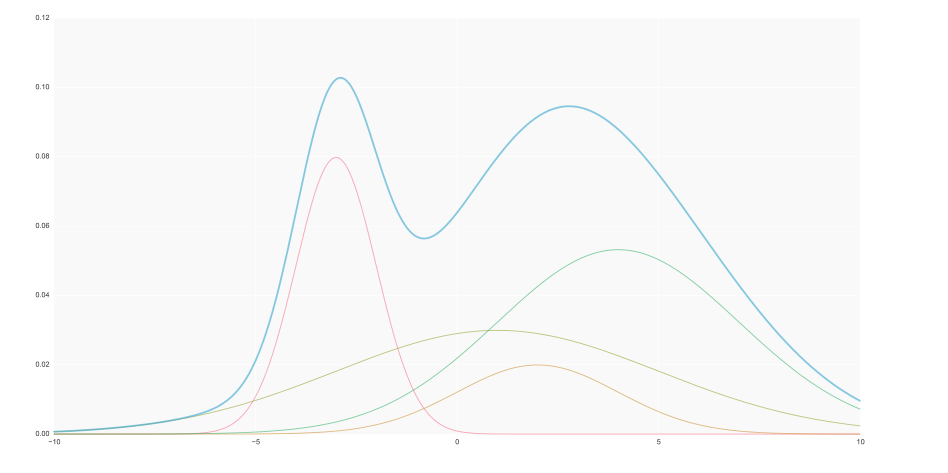
È possibile dimostrare che quasi tutte le distribuzioni continue possono essere ottenute tramite una combinazione lineare di un numero abbastanza grand di gaussiane.
2 Mixture Parameters Estimation
Fissato il valore \(K\), dato un dataset \(\mathbf{X} = (x_1, \ldots, x_n)\), i parametri \(\pi\) e \(\theta\) di una mistura di \(K\) elementi possono essere stimati tramite la maximum likelihood
\[L(\theta, \pi | \mathbf{X}) = p(\mathbf{X} | \theta, \pi)$ = \prod\limits_{i = 1}^n p(x_i | \theta, \pi) = \prod\limits_{i = 1}^n \sum\limits_{k = 1}^K \pi_k \cdot q(x | \theta_k)\]
passando alla log-likelihood
\[\begin{split} l(\theta, \pi | \mathbf{X}) &= \log{p(\mathbf{X}|\theta, \pi)} \\ &= \sum\limits_{i = 1}^n \log{p(x_i|\theta, \pi)} \\ &= \sum\limits_{i = 1}^n \log{\Bigg(\sum\limits_{k = 1}^K \pi_k \cdot q(x_i | \theta_k) \Bigg)} \\ \end{split}\]
La massimizzazione della log-likelihood deve poi essere effettuata sotto i vincoli \(0 \leq \pi_i \leq 1\) e \(\sum_{i = 1}^K \pi_i = 1\). Applicando il metodo dei moltiplicatori di lagrange otteniamo il seguente problema di massimizzazione
\[\mathcal{L}(\theta, \pi, \lambda) = l(\theta, \pi | \mathbf{X}) + \lambda \cdot \Bigg(1 - \sum\limits_{i = 1}^K \pi_i \Bigg)\]
2.1 Respect to \(\pi\)
Andiamo quindi a considerare le derivate rispetto ai vari pesi \(\pi\)
\[\frac{\partial \mathcal{L}(\theta, \pi | \mathbf{X})}{\partial \pi_j} = \frac{\partial l(\theta, \pi | \mathbf{X})}{\partial \pi_j} - \lambda = 0\]
continuando i calcoli
\[\begin{split} \lambda = \frac{\partial l(\theta, \pi | \mathbf{X})}{\partial \pi_j} &= \frac{\partial}{\partial \pi_j} \Bigg[\sum\limits_{i = 1}^n \log{\Bigg(\sum\limits_{k = 1}^K \pi_k q(x_i|\theta_k) \Bigg)} \Bigg] \\ &= \sum\limits_{i = 1}^n \frac{\partial}{\partial \pi_j} \Bigg[ \log{\Bigg(\sum\limits_{k = 1}^K \pi_k q(x_i | \theta_k) \Bigg)}\Bigg] \\ &= \sum\limits_{i = 1}^n \frac{1}{\sum_{k = 1}^K \pi_k q(x_i | \theta_k) } \cdot \frac{\partial}{\partial \pi_j} \Bigg(\sum\limits_{k = 1}^K \pi_k q(x_i | \theta_k)\Bigg) \\ &= \sum\limits_{i = 1}^n \frac{1}{\sum_{k = 1}^K \pi_k q(x_i | \theta_k) } \cdot \sum\limits_{k = 1}^K \frac{\partial}{\partial \pi_j} \Bigg( \pi_k q(x_i | \theta_k)\Bigg) \\ &= \sum\limits_{i = 1}^N \frac{q(x_i | \theta_j)}{\sum_{k = 1}^K \pi_k q(x_i | \theta_k)} \\ &= \sum\limits_{i = 1}^n \frac{\gamma_j(x_i)}{\pi_j} \\ &= \frac{1}{\pi_j} \sum\limits_{i = 1}^n \gamma_j(x_i) \\ \end{split}\]
dove
\[\gamma_k(x) = \frac{\pi_k \cdot q(x | \theta_k)}{\sum_{j = 1}^K \pi_j \cdot q(x | \theta_j)}\]
2.2 Respect to \(\lambda\)
Considerando invece la derivata rispetto a \(\lambda\) e ponendola uguale a \(0\) otteniamo
\[\frac{\partial \mathcal{L}(\theta, \pi | \mathbf{X}}{\partial \lambda} = \frac{\partial}{\partial \lambda}\Bigg(l(\theta, \pi | \mathbf{X}) + \lambda \Big(1 - \sum\limits_{i = 1}^K \pi_i \Big) \Bigg) = 0\]
il che equivale a dire
\[\sum\limits_{i = 1}^K \pi_i = 1\]
2.3 Combining
Componendo i due ultimi risultati otteniamo
\[\sum\limits_{j = 1}^K \pi_j = \frac{1}{\lambda} \sum\limits_{j = 1}^K \sum\limits_{i = 1}^n \gamma_j(x_i) = 1\]
il che implica
\[\begin{split} \lambda = \sum\limits_{j = 1}^K \sum\limits_{i = 1}^n \gamma_j(x_i) &= \sum\limits_{i = 1}^n \sum\limits_{j = 1}^K \gamma_j(x_i) \\ &= \sum\limits_{i = 1}^n \sum\limits_{j = 1}^K \frac{\pi_j q(x_i | \theta_j)}{\sum_{k = 1}^K \pi_k q(x_i | \theta_k)} \\ &= \sum\limits_{i = 1}^n 1 \\ &= n \end{split}\]
e quindi
\[\pi_k =\frac{1}{n} \sum\limits_{i = 1}^n \gamma_k(x_i)\]
Notiamo quindi che per ogni elemento della mistura \(j=1,\ldots,k\) considero sia il peso della combinazione lineare \(\pi_j\) che la funzione \(\gamma_j(x_i)\).
2.4 Respect to \(\theta\)
Infine, per quanto riguarda le derivata rispetto ai parametri \(\theta\), otteniamo
\[\begin{split} \frac{\partial \mathcal{L}(\theta, \pi | \mathbf{X})}{\partial \theta_j} &= \frac{\partial}{\partial \theta_j} \Bigg[ \sum\limits_{i = 1}^n \log{\Bigg(\sum\limits_{k = 1}^K \pi_k \cdot q(x_i | \theta_k) \Bigg)} \Bigg] \\ &= \sum\limits_{i = 1}^n \frac{\partial}{\partial \theta_j} \Bigg[\log{\Bigg( \sum\limits_{k = 1}^K \pi_k \cdot q(x_i | \theta_k) \Bigg)} \Bigg] \\ &\;\; \vdots \\ &= \sum\limits_{i = 1}^n \gamma_j(x_i) \cdot \frac{\partial \log{q(x_i | \theta_j)}}{\partial \theta_j} = 0 \\ \end{split}\]
2.5 Analytical Intractability
Notiamo a questo punto che andare a massimizzare la log-likelihood in modo analitico (in forma chiusa) non è possibile, in quanto
\(\pi\) e \(\theta\) possono essere derivati da \(\gamma_k(x_i)\)
\(\gamma_k(x_i)\) può essere derivata da \(\pi\) e \(\theta\).
Per risolvere questo problema si procedere quindi in modo iterativo nel seguente modo:
Si fissa una stima per \(\pi\) e \(\theta\), ovvero si ipotizza come è fatta la mistura.
A partire da queste si stimano tutte le funzioni \(\gamma_k(x_i)\)
A partire da questa si derivano delle nuove stime per \(\pi\) e \(\theta\)
e via dicendo, iterando questo procedimento.
3 Mixtures as Generative Process
Consideriamo adesso la mistura come un processo generativo, ovvero consideriamo una mistura come una tecnica per generare un insieme di dati.
Il processo di generazione può essere raffiturato tramite un modello grafico come quello riportato a seguire
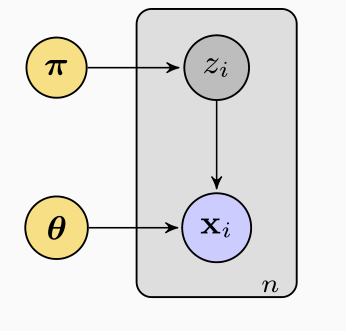
Questo modello mostra le relazioni in gioco tra le varie variabili casuali e parametri presenti all'interno del nostro modello probabilistico.
Tutti i nodi del grafico rappresentano variabili casuali e/o parametri. I nodi in giallo rappresentano i parametri. Il box rappresenta il fatto che a partire da \(\pi\) e \(\theta\) abbiamo \(n\) variabili \(z_1, \ldots, z_n\) e \(n\) variaibli \(x_1, \ldots, x_n\).
La generazione di un dataset \(x_1, \ldots, x_n\) tramite una mistura si basa sull'iterazione della seguente procedura
Considero il vettore \(\pi\) come un vettore di \(k\) valori di probabilità \(\pi_1, \ldots, \pi_k\).
A partire da \(\pi\) genero la v.a. \(z_i \in \{1, \ldots, k\}\) in modo tale che la probabilità che \(z_i = j\) è proprio \(\pi_j\) per \(j = 1,\ldots,k\). Il valore di \(z_i\) che ho generato determina la particolare distribuzione dalla mistura che utilizzerò per generare \(x_i\).
A partire dalla \(z_i\) scelta quindi, \(x_i\) verrà generato con la distribuzione \(q(x | \theta_{z_i})\).
Notiamo la diversa funzione delle variabili \(x_i\) e \(z_i\): mentre sono in grado di osservare il valore di \(x_i\), il valore di \(z_i\) non viene osservato nel momento in cui considero i dati generati. Per questa ragione le variabili \(x_i\) si dicono variabili osservabili, mentre le variabili \(z_i\) sono dette variabili latenti.
3.1 Example
Il seguente esempio mostra la generazione di un dataset utilizzando una mistura di \(3\) gaussiane.
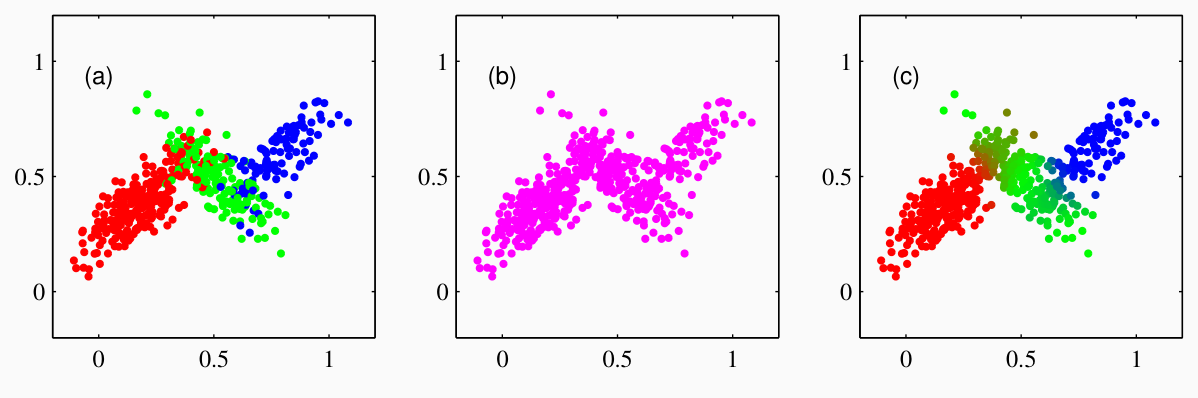
Notiamo che nella figura più a sinistra abbiamo acesso sia a \(z_1, \ldots z_n\) che \(x_1, \ldots, x_n\), mentre la figura al centro corrisponde ad avere accesso solamente ai valori \(x_i\).
La combinazione tra valori osservabili e valori latenti prende il nome di dataset completo, ed è un'astrazione, in quanto i valori \(z_1, \ldots, z_n\) non sono valori fisicamente reali, ma rappresentano un modello per generare i dati \(x_1, \ldots, x_n\).
Infine, la figura a destra rappresenta un processo di inferenza in cui a partire dai soli dati osservati \(x_i\), si stima la probabilità che quel punto derivasse da ognuna delle \(3\) gaussiane utilizzate nella mistura.
3.2 Probabilistic Clustering
Riflettendo sull'ultimo esempio è possibile osservare che con questo approccio a partire dal nostro dataset abbiamo ottenuto una descrizione probabilistica del clusterting.
In particolare abbiamo,
Una descrizione probabilistica associata ad ogni distribuzione facente parte della mistura. Questa descrizione è paragonabile al prototipo che abbiamo introdotto nella discussione del clusterting deterministico.
Per ogni elemento poi, abbiamo un valore di probabilità per ogni distribuzione, ovvero per ogni cluster, che rappresenta proprio la probabilità che quell'elemento appartiene a quel cluster. Così facendo abbiamo ottenuto una descrizione probabilistica di un clustering.
3.3 Distributions with latent variables
Analizziamo adesso più precisamente questa situazione di distribuzione con variabili latenti. Per come è stato definito il nostro modello abbiamo che
\[p(x | z = k, \theta, \pi) = p(x | z = k, \theta) = q(x | \theta_k)\]
se poi calcoliamo la marginalizzazione rispetto a \(z\) otteniamo
\[\begin{split} p(x | \theta, \pi) &= \sum\limits_{k = 1}^K p(x, z=k | \theta, \pi) \\ &= \sum\limits_{k = 1}^K p(x | z = k, \pi, \theta) \cdot p(z = k | \theta, \pi) \\ &= \sum\limits_{k = 1}^K (p | z = k, \theta) \cdot p(z = k | \pi) \\ &= \sum\limits_{k = 1}^K q(x | \theta_k) \cdot p(z = k | \pi) \\ \end{split}\]
Dato poi che per definizione abbiamo che
\[p(x | \theta, \pi) = \sum\limits_{k = 1}^K \pi_k \cdot q(x_i | \theta_k)\]
otteniamo
\[\pi_k = p(z = k | \pi)\]
Possiamo quindi interpretare il valore \(\pi_k\) come il valore di probabilità che il prossimo punto viene generato utilizzando la \(k\) esima distribuzione della mistura.
Collegata a questa interpretazione possiamo poi interpretare le funzioni \(\gamma_k(x)\) come segue
\[\begin{split} \gamma_k(x) &= \frac{\pi_k \cdot q(x | \theta_k) }{\sum_{j = 1}^K \pi_j q(x | \theta_j)} \\ &= \frac{p(z = k) \cdot p(x | z = k)}{\sum_{j = 1}^K p(z = j) p(x | z = j)} \\ &= p(z = k | x) \\ \end{split}\]
quindi \(\gamma_k(x)\) è la probabilità a posteriori che l'elemento considerato è stato generato con la \(k\) esima distribuzione. Dunque mentre \(\pi_k\) è la probabilità a priori, \(\gamma_k(x)\) è quella a posteriori. Il valore \(\gamma_k(x)\) è detto responsibility.
4 Mixtures of Gaussian Distribution
Nel caso delle distribuzioni gaussiane abbiamo che
\[q(x | \theta_k) = \mathcal{N}(x | \mu_k, \Sigma_k)\]
e quindi
\[\gamma_k(x) = \frac{\pi_k \cdot \mathcal{N}(x|\mu_k, \Sigma_k)}{\sum_{j = 1}^K \pi_j \mathcal{N}(x | \mu_j, \Sigma_j)}\]
e la likelihood è massimizzata per
\[\begin{split} \pi_j &= \frac{1}{n} \sum\limits_{i = 1}^n \gamma_j(x_i) \\ \\ \sum\limits_{i = 1}^n &\gamma_j(x_i) \cdot \Big[ \frac{\partial }{\partial \theta_j} \log{\mathcal{N}(x_i | \mu_j, \Sigma_j)} \Big] = 0 \\ \end{split}\]
i valori di interesse quindi sono derivanti da questa coppia di equazioni.