MVS - 01 - Introduzione
Lecture Info
Dates:
Introduction: In questa lezione abbiamo introdotto l'obiettivo del corso, portando qualche esempio di modellizzazione di sistemi tramite l'utilizzo di automi a stati finiti.
1 Introduzione al corso
In questo corso studieremo il model checking, che consiste nello studio di modelli e algoritmi che permettono la verifica formale di determinate proprietà all'interno sistema critico.
Notiamo, a tale scopo, che c'è una profonda differenza tra il tipo di verifica sistematica offerto dal model checking e l'approccio più tradizionalmente preso dall'ingegneria del software, che consiste invece di effettuare un testing estensivo. Il testing infatti, oltre che ad essere estremamente costo e inefficiente, non basta alle esigenze della società moderna. Piuttosto che effettuare un testing massivo siamo quindi interessati a costruire dei certificati di correttezza, sia per la parte hardware e sia per la parte software.
Il testing può rilevare la presenza di errori ma non la loro assenza.
Djikstra.
Per completezza, notiamo che un ulteriore approccio potrebbe essere quello di certificare i processi. Per fare un esempio, consideriamo i vaccini. Per certificare i vaccini si utilizzano delle certificazione dei processi, che impongono dei vincoli molto stretti sui processi che portano alla creazione di un nuovo futuro vaccino. L'unica cosa che può essere fatta in questi casi è definire un processo di gestione e attenersi rigorosamente alle regole.
Il corso però non si basa né sulla certificazione dei processi né su un testing massivo. L'idea invece è quella di fare una verifica sistematica per produrre un certificato di correttezza rispetto a certe proprietà del nostro sistema.
Per poter fare questo il primo passo è quello di definire un modello del sistema. Come strumento fondamentale per questo passo di modellizzazione utilizzeremo i classici automi a stati finiti. I nostri automi saranno però leggermente diversi da quelli studiati in un tipico corso di fondamenti di informatica. Gli atomi tradizionali infatti sono automi che accettano un particolare linguaggio; i nostri automi invece devono operare in un ciclo infinito.
2 Esempi
Terminiamo questa lezione con qualche esempio dimostrativo.
2.1 Termometro
Termometro con \(3\) cifre: \(1000\) stati possibili. Possiamo mettere un range per la temperatura. Per la trasmissione dei dati abbiamo possiamo avere varie possibilità:
Comunicare sempre i dati, ma questo porta ad un problema di batteria.
Creare una connessione una volta che sono stati misurati dei dati e inviarla all'assistente hardware in modo da minimizzare l'energia sprecata.
L'idea è quella di modelizzare questo componente con un automa a stati finiti. Una volta che abbiamo formalizzato il nostro sistema tramite un automa, gli algoritmi di verifica che andremo a vedere lavorano tutti partendo da uno stato di flattering.
Flattering: siccome le variabili globali non hanno nessun
significato se non dal punto di vista della fotografia del sistema,
il flattering consiste nell'avere, per ogni stato del sistema un
relativo stato dell'automa. Nell'esempio del termometro la variabile
k , che indica il timeout, varia tra 0 e 20. La variabile temp_m
varia tra 35.0 a 39.9. Nel flattering quindi espandiamo il valore di
queste variaibli, avendo uno stato per ogni possibile combinazione
di valori.
2.2 Controllore di Accesso
Consideriamo il seguente atoma che regola l'accesso ad una porta. La porta può essere aperta solamente digitando la corretta sequenza \(\text{ABA}\). Assumiamo inoltre che l'utente può fare un arbitrario numero di tentativi, ovvero che non ci siano meccanismi di blocco.
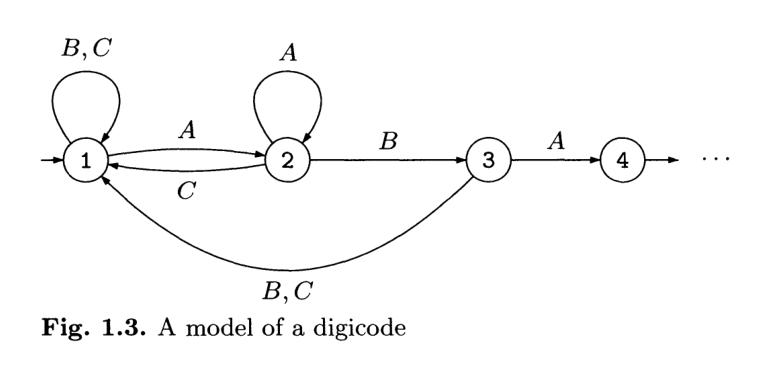
La verifica automatica è la dimostrazione automatica del fatto che una data proprietà (la specifica) sia verificata oppure no. Per fare questo, o dimostriamo cha la proprietà (la specifica) sia vera, oppure riportiamo un controesempio, ovvero una possibile esecuzione dell'automa su cui la specifica non vale.
Def: Una esecuzione di un automa a stati finiti è una sequenza di stati che descrive una possibile evoluzione del sistema. L'insieme di tutte le possibili esecuzioni viene rappresentato tramite un execution tree (albero delle esecuzioni).
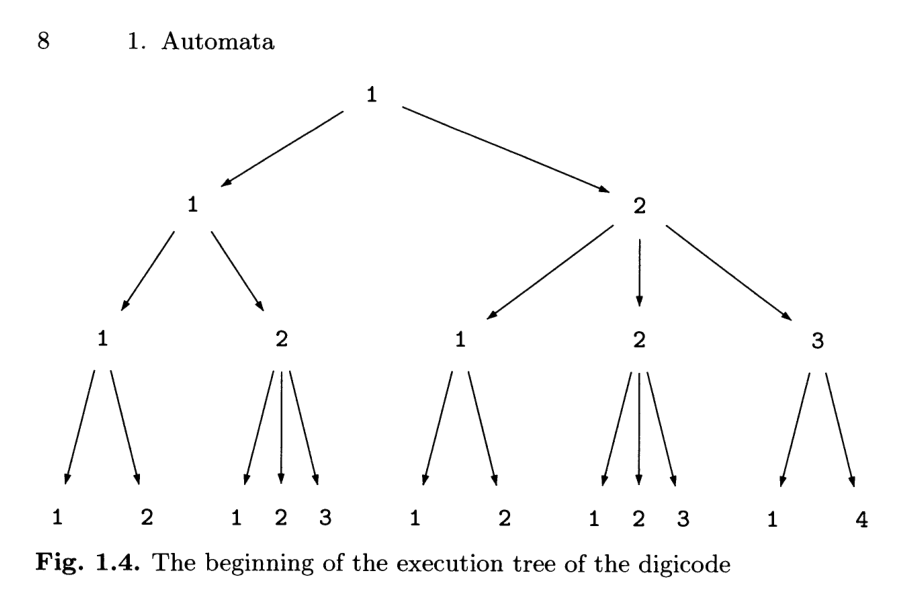
Per rendere il processo di specifica automatico dobbiamo aggiungere delle proprietà elementari al nostro automa. Queste proprietà vivono all'interno degli stati del nostro automa, possono essere vere o false, a seconda se sono o meno verificate, e sono anche chiamate osservabili.
Rispetto all'automa dell'esempio, possiamo considerare ad esempio le seguenti proprietà.
\(P_{\text{open}}\): Questa proprietà rappresenta il fatto che la porta è aperta. È vera solamente nello stato \(4\), mentre è falsa negli stati \(1, 2, 3\).
\(P_A\): Sono entrato nello stato corrente perché è stato digitato il carattere \(A\). Questa proprietà è vera negli stati \(4\) e \(2\).
\(P_B\): Sono entrato nello stato corrente perché è stato digitato il carattere \(B\). Questa proprietà è vera negli stati \(3\). Non è vera nello stato \(1\) in quanto posso arrivare nello stato \(1\) anche digitando \(C\).
\(P_C\): Sono entrato nello stato corrente perché è stato digitato il carattere \(C\).
\(\text{pred}_2\): Lo stato precedente in una qualsiasi esecuzione è \(2\). Questa proprietà è vera nello stato \(3\).
\(\text{pred}_3\): Lo stato precedente in una qualsiasi esecuzione è \(3\). Questa proprietà è vera nello stato \(4\).
Una volta che abbiamo formalizzato tutte queste proprietà possiamo dimostrare il fatto che la porta si apre se e solo se digitiamo la sequenza corretta.
Dim: Consideriamo una qualsiasi esecuzione che ci porta ad aprire la porta, ovvero allo stato \(4\).
Dato che la proprietà \(\text{pred}_3\) vale nello stato \(4\), questa esecuzione deve terminare con la sequenza di stati \(3 \to 4\). Continuando, nello stato \(3\) vale \(\text{pred}_2\), dunque l'esecuzione finisce con la sequenza \(2 \to 3 \to 4\). Infine, dato che \(P_A\) vale in \(2\) e \(4\) e \(P_B\) vale in \(3\), otteniamo che gli ultimi tre caratteri digitati sono \(\text{A, B, A}\).
\[\tag*{$\blacksquare$}\]
Così facendo abbiamo dimostrato che se la porta si apre, allora la sequenza corretta è stata digitata. La dimostrazione del lato opposto è banale: basta vedere l'automa per capire che digitando la sequenza \(\{A, B, A\}\) terminiamo nello stato \(4\), in cui vale la proprietà \(P_{\text{open}}\).