MVS - 02 - Automi di Verifica
Lecture Info
Date:
Introduction: Nella scorsa lezione avevamo introddo in generale gli obiettivi del corso. In questa lezione definiamo formalmente gli automi che andremo ad utilizzare durante il corso.
1 Definizione di Automa
Le macchine che studiamo sono re-attive, come il distributore di bevante o il sistema di controllo di accesso automatico di una porta. Stando in un certo stato ricevono un evento, fanno una certa azione. Formalmente i nostri automi sono definiti come segue
Def: Dato un insieme di proprietà elementari \(Prop = \{P_1, P_2, \ldots\}\), un automa è una tupla
\[\mathcal{A} = \langle Q, E, T, q_0, l\rangle\]
dove,
\(Q\) è un insieme finito di stati.
\(E\) è un insieme finito di transition labels (etichette per transizioni).
\(T \subseteq Q \times E \times Q\) è l'insieme delle transazioni.
\(q_0\) è lo stato iniziale dell'automa.
\(l(\cdot)\) è una funzione che mappa a ciascun stato \(q \in Q\) l'insieme di proposizioni elementari (dette osservabili) \(l(q) \in Prop\) che valgono in quel particolare stato.
A seguire riportiamo qualche concetto utile legato al comportamento di un automa:
Un cammino (path) di un automa \(\mathcal{A}\) è una sequenza \(\sigma\), finita o infinita, di transizioni \((q_i, e_i, q_i^{'})\) tali che \(q_i^{'} = q_{i+1}\) per ogni \(i\). Tipicamente un cammino è denotato come segue
\[q_1 \overset{e_1}{\to} q_2 \overset{e_2}{\to} q_3 \overset{e_3}{\to} \ldots \]
La lunghezza di un cammino \(\sigma\), denotata con \(|\sigma|\) è un numero, potenzialmente infinito, che rappresenta il numero di transizioni del cammino. L'i-esimo stato del cammino \(\sigma\), denotato con \(\sigma(i)\), è lo stato \(q_i\).
Una esecuzione parziale è una qualsiasi esecuzione che inizia dallo stato iniziale \(q_0\).
Una esecuzione completa è una esecuzione massimale, ovvero che non può essere estesa.
Uno stato è raggiungibile (reachable) se appare nell'albero di esecuzione dell'automa, ovvero se esiste almeno una esecuzione nella quale appare.
Per terminare, consideriamo la seguente proprietà, che differenzia profondamente i nostri automi da quelli studiati più formalmente dall'informatica.
Liveness property: An automaton always eventually performs yet another transition.
2 Esempi
Terminiamo la lezione con i seguenti due esempi.
2.1 Controllore di Accesso
Volendo fare un esempio, consideriamo l'automa visto la scorsa lezione per gestire il controllo di una porta automatica. L'automa era stato rappresentato nel seguente modo
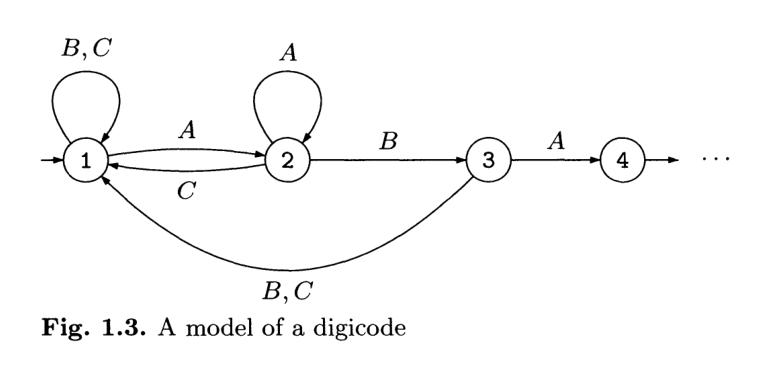
Volendo formalizzarlo utilizzando la definizione appena data otteniamo
L'insieme degli stati possibili è dato da
\[Q = \{1, 2, 3, 4\}\]
L'insieme delle etichette per le varie transizioni è dato da
\[E = \{A, B, C\}\]
Lo stato iniziale è
\[q_0 = 1\]
La funzione di transizione è
\[\begin{split} T = &\{(1, A, 2), (1, B, 1), (1, C, 1), \\ &(2, A, 2), (2, B, 3), (2, C, 1), \\ &(3, A, 4), (3, B, 1), (3, C, 1)\} \end{split}\]
La funzione \(l(\cdot)\) è data da
\[l = \begin{cases} 1 &\to \emptyset \\ 2 &\to \{P_A\} \\ 3 &\to \{P_B, \text{pred}_2\} \\ 4 &\to \{P_A, \text{pred}_3\} \\ \end{cases}\]
Se vogliamo unire la rappresentazione grafica data come con le informazioni aggiuntive date dalla funzione \(l(\cdot)\), ovvero con la conoscenza delle proprietà elementari che valgono in ogni stato, possiamo utilizzare la seguente rappresentazione
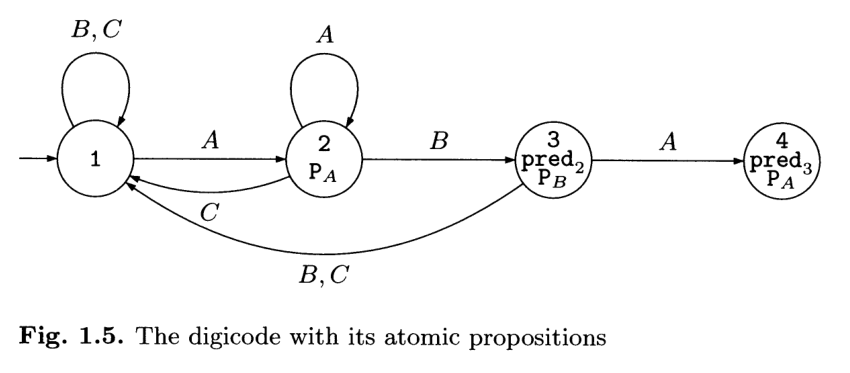
2.2 Printer Manager
Consideriamo il seguente automa, che viene utilizzato per gestire la condivisione di una stampante tra due utenti
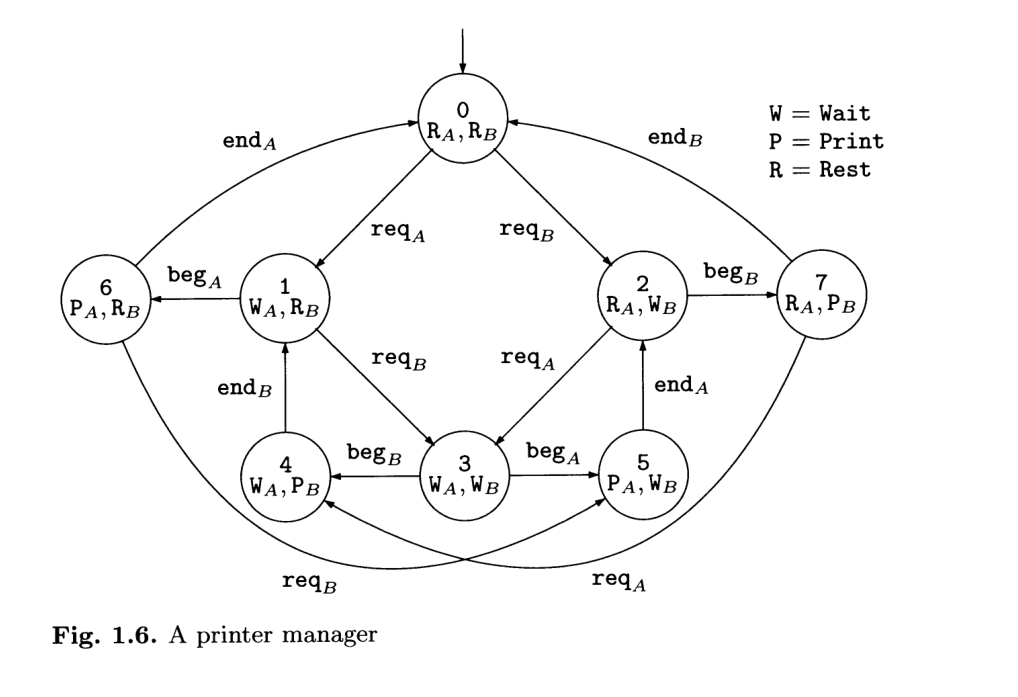
Descriviamo quindi le varie proprietà atomiche:
\(W_A\): Una richiesta da processare è stata inviata dall'utente \(A\).
\(W_B\): Una richiesta da processare è stata inviata dall'utente \(B\).
\(P_A\): La stampante sta stampando un documento dell'utente \(A\).
\(P_B\): La stampante sta stampando un documento dell'utente \(B\).
\(R_A\): Non ci sono richieste di stampda da parte dell'utente \(A\).
\(R_B\): Non ci sono richieste di stampda da parte dell'utente \(B\).
Ora che abbiamo completamente modellato il nostro printer manager, possiamo studiare alcune proprietà di questo modello. Due proprietà interessanti da studiare ad esempio sono le seguenti:
Correttezza: l'abitraggio che sta eseguendo è corretto, ovvero siamo sicuri che non sia possibile simultaneamente la stampa di entrambi gli utenti.
Fairness: Nessuno muore di fame, se io chiedo di accedere ad una risorsa prima o poi accederò alla risorsa.
Alcune di queste proprietà potrebbe essere proprietà locale, nel senso che sono verificabili guardando solamente il singolo stato. Altre invece potrebbero essere proprietà globale, nel senso che per verificarle devo guardare anche altri stati.