MVS - 03 - Problema della Verifica

• Date: [2020-10-28 mer 11:30]

• Slides:

• Introduction:

Consideriamo l'automa della stampa che avevamo visto la scorsa lezione

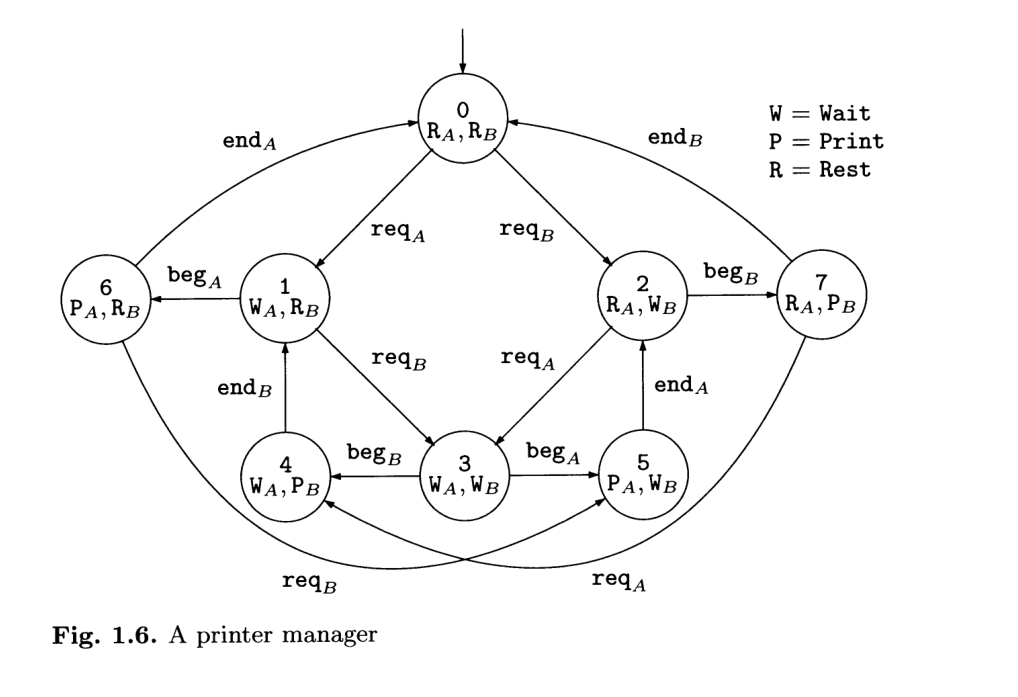
Il problema della verifica deve partire da una codificazione delle proprietà atomiche del sistema. Il problema della verifica è ben posto quando abbiamo definito chiaramente cosa siano gli osservabili. Quello che voglio verificare lo esprimo in proprietà atomiche.

Per formalizzare e rendere automatico questo controllo l'idea è quella di utilizzare dei bits per le varie proprietà atomiche della stampa \(R_A\), \(W_A\), \(P_A\), \(R_B\), \(W_B\), \(P_B\). A ciascun stato assegno quindi una sequenza di bits. Successivamente poi, fissato uno stato, posso utilizzare questa sequenza di bits per controllare in modo immediato quali proprietà atomiche vivono nello stato. Ad esempio potrei controllare la seguente condizione

\[\neg (P_A \land P_B)\]

che mi permettere se nello stato che sto considerando il sistema sta stampando contemporaneamente per entrambi gli utenti.

Oppure consideriamo la seguente ulteriore proprietà: "Se l'evento \(P_A\) si verifica in un certo stato \(q\) allora in un qualche stato precedente vale \(W_A\)". Notiamo che questa proprietà non è più atomica, come la precedente, in quanto per verificarla necessito di verificare più stati. Questa proprietà può essere verificata come segue:

1. Esploro tutti i possibili stati e vedo quelli in cui \(P_A\) è vera.

2. Per ogni stato in cui \(P_A\) è vero mi vedo solo gli stati entranti.

3. Per ogni stato entrante verifico se \(P_A\) continua ad essere vero. Appena \(P_A\) non è più vero verifico she \(W_A\) è vero.

Per terminare, un'ulteriore proprietà interessante è la seguente.

Proprietà di Fairness: Se in un certo stato \(q\) vale \(W_A\), allora in tutti i cammini sigma che partono da \(S\) esiste un \(i\) tale che in \(\sigma(i)\) vale \(P_A\).

Notiamo che questa proprietà non è garantita, in quanto esiste un cammino in cui sia \(A\) che \(B\) richiedono la stampa, ma solamente le richieste di \(B\) vengono continuamente soddisfatte.

Quando impostiamo il problema della verifica i sistemi che andiamo a verificare possono essere rappresentati in vari modi. La verifica nasce da una certa descrizione del sistema, che può essere data in vari modi. In ogni caso, per poter applicare la tecnologia del model checking, dobbiamo ragionare con il sistema appiattito tramite la procedura che noi chiamiamo flattening.

Il flattening è legato alla reachability analysis, che consiste nel capire quali stati sono raggiungibili dallo stato iniziale mediante transizioni legali. Il flattering è un processo cieco, che trova i vari stati solamente esplorando l'automa e tutti i possibili valori per le variabili globali. Risulta quindi fondamentale ricordarsi degli stati che sono stati già scoperti, e per fare questo dobbiamo controllare se lo stato è già presente in memoria.