MVS - 04 - Sincronizzare gli Automi
Lecture Info
Date:
Introduction: In questa lezione abbiamo trattato il problema di modellare sistemi complessi tramite l'utilizzo di più automi, e di come poter sincronizzare questi automi tra loro.
1 Come Sincronizzazione
Molto spesso dobbiamo verificare alcune proprietà di sistemi complessi. Tipicamente questi sistemi possono essere spezzati in vari componenti, ciascuno dei quali può essere modellato tramite un automa a stati finiti. Per modellare l'intero sistema quindi questi automi vengono amalgamenti tra loro mediante un processo di sincronizzazione.
La sincronizzazione può essere ottenunta in vari modi, tra cui troviamo:
Tramite il prodotto cartesiano.
Tramite lo scambio di messaggi.
Tramite l'utilizzo di variabili condivise.
L'esempio più facile di sincronizzazione è quando il sistema può essere spezzato in compomenti indipendenti, ovvero componenti che non interagiscono tra loro. In questi casi l'automa globale è ottenuto dal prodotto cartesiano degli automi che rappresentano i vari componenti, e che andremmo a definire formalmente a seguire.
2 Prodotto Cartesiano tra Automi
Consideriamo una famiglia di \(n\) automi, in cui ogni \(i \in \{1, \ldots, n\}\) definisce un automa
\[\mathcal{A}_i = \langle Q_i, E_i, T_i, q_{0,i}, l_i\rangle\]
e introduciamo una nuova etichetta per le transizioni \(-\) che rappresenta l'azione "non fare nulla" per tutti gli automi che non vengono utilizzati durante una transizione globale tra l'insieme dei componenti del sistema.
Il prodotto cartesiano di questi automi è l'automa
\[\mathcal{A}_1 \times \mathcal{A}_2 \times \ldots \mathcal{A}_n = \mathcal{A} = \langle Q, E, T, q_0, l\rangle\]
dove,
L'insieme degli stati è il prodotto cartesiano degli insiemi degli stati dei vari automi
\[Q = Q_1 \times Q_2 \ldots \times Q_n\]
Le etichette per le transizioni sono ottenute prendendo il prodotto cartesiano delle etichette dei vari automi, in cui pero aggiungiamo anche la possibilità di avere il valore \(-\) a ciascun automa.
\[E = \prod\limits_{1 \leq i \leq n} (E_i \cup \{-\})\]
L'insieme delle transizioni \(T\) è dato da tutte le transazioni della forma
\[(q_1, q_2, \ldots, q_n) \overset{(e_1, e_2, \ldots, e_n)}{\longrightarrow} (q_1^{'}, q_2^{'}, \ldots, q_n^{'})\]
dove per ogni automa \(i\) vale una delle seguenti condizioni:
L'automa \(i\) esimo non fa nulla, e quindi \(e_i = \text{-}\) e \(q_i^{'} = q_i\)
L'automa \(i\) effettua una transizione,e quindi \(e_i \neq \text{-}\) e \((q_i, e_i, q_i^{'}) \in T_i\), ovvero tale transazione è valida rispetto alle regole di transazioni di \(i\).
Lo stato iniziale del prodotto cartesiano è ottenuto prendendo gli stati iniziali di tutti gli automi
\[q_0 = (q_{0, 1}, q_{0, 2}, \ldots, q_{0, n})\]
Le proposizioni atomiche valide nello stato \((q_1, q_2, \ldots, q_n)\) sono ottenute prendendo l'unione delle proposizioni atomiche valide in ciascun \(q_i\). Formalmente,
\[l((q_1, \ldots, q_n)) = \bigcup\limits_{i \leq i \leq n} l_i(q_i)\]
Notiamo che nella definizione appena data non c'è nessun tipo di sincronizzazione tra i vari automi. Per sincronizzare i vari componenti si procede quindi restringendo l'insieme delle possibili transizioni tramite un synchronization set
\[\text{Sync} \subseteq \prod_{1 \leq i \leq n} (E_i \cup \{-\})\]
Questo insieme contiene tutte le etichette degli archi (labels) che sono permessi dalla sincronizzazione. Una volta introdotto questo insieme quindi possiamo restringere tutte le transazioni possibili
\[((q_1, \ldots, q_n), (e_1, \ldots, e_n), (q_1^{'}, \ldots, q_n^{'})) \in T\]
richiedendo come prima condizione che \((e_1, \ldots, e_n) \in \text{Sync}\).
3 Esempi di Sincronizzazione
Andiamo adesso a mostrare un esempio di sincronizzazione per ogni possibile modo di sincronizzare i nostri automi.
3.1 Sincronizzazione tramite messaggi
Un caso particolare della sincronizzazione tramite prodotto cartesiano è fornito dal framework del message passing. In questo particolare caso distinguiamo tra le etichette delle transazioni quelle associate all'emissione di un messaggio \(m\), denotate con \(!m\), e quelle associate alla ricezione di questo messaggio, denotate con \(?m\).
Per riportare un esempio concreto, consideriamo la modellazione di un ascensore in un edificio con 3 diversi piani. L'ascensore sarà modellato utilizzanto i seguenti componenti:
La cabina: la cabina può andare in alto o in basso, a seconda del piano in cui si trova e dei comandi inviati dal controllore. La cabina è modellata dal seguente automa.
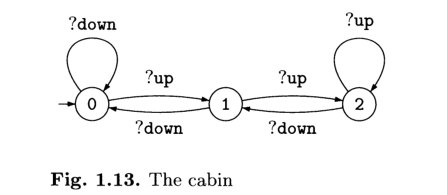
Le tre porte: una per piano, possono aprirsi e chiudersi a seconda dei comandi del controllore. Ciascuna porta è modellata dal seguente automa, per \(i \in \{0, 1, 2\}\).
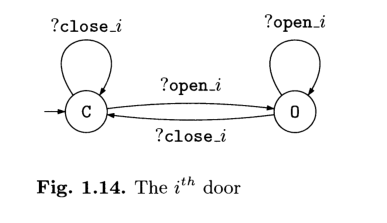
Il controllore: utilizzato per inviare i comandi alle tre porti e alla cabina. Il controllore è modellato dal seguente automa.
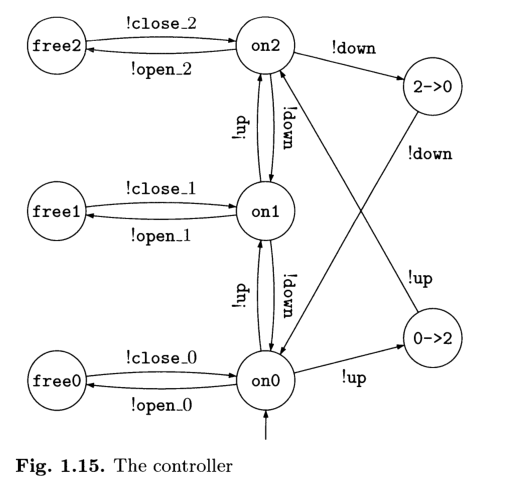
Notiamo come il controllore comanda i vari componenti tramite l'inivio di messaggi. Per modellare l'intero sistema quindi l'idea è quella di calcolare il prodotto cartesiano di questi automi. Lo stato globale del sistema è quindi specificato da cinque componenti, che corrispondono, rispettivamente, a
Lo stato della porta numero \(0\)
Lo stato della porta numero \(1\)
Lo stato della porta numero \(2\)
Lo stato della cabina
Lo stato del controllore
Per sincronizzare l'intero sistema poi dobbiamo imporre il seguente insieme synchronization set, che ci permette di sincronizzare l'invio dei messaggi da parte del controllore con la relative ricezione da parte dei vari componenti. Nel nostro particolare caso troviamo

Una volta che abbiamo modellato questo sistema, possiamo chiederci se, ad esempio, questo ascensore può essere considerato funzionale, ovvero se può essere utilizzato senza rischio. A tale fine potremmo voler verificare una serie di proprietà interessanti, tra cui troviamo anche le seguenti:
\((P_1)\): La porta di ogni piano si può aprire se e solo se la cabina si trova in quel particolare piano.
\((P_2)\): La cabina non si può muovere se la porta del piano in cui si trova è attualmente aperta.
Tramite un model checker siamo in grado di dimostrare se queste proprietà vengono verificate oppure no.
3.2 Sincronizzazione tramite Variabili Condivise
Un ulteriore modo per far comunicare componenti di un sistema complesso tra loro è tramite l'introduzione di variabili condivise. A tale fine consideriamo nuovamente il caso in cui due utenti \(A\) e \(B\) condividono una stampante. L'idea quindi è di utilizzare una variabile condivisa che determina l'utente che in un dato momento può stampare.
In particolare quindi troviamo il seguente automa per l'utente \(A\)
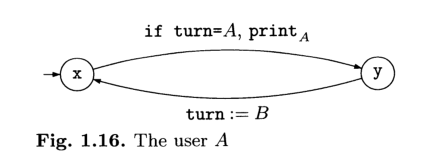
per l'utente \(B\) ovviamente abbiamo un automa simmetrico a quello di \(A\)
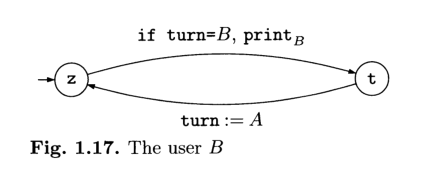
L'automa globale che descrive il sistema è quindi il seguente
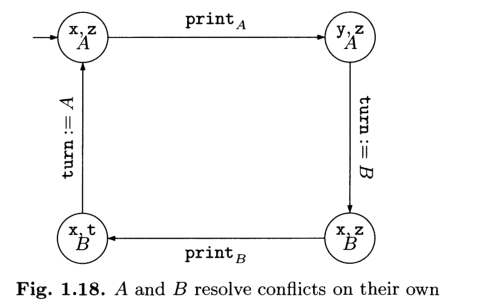
Questo modello garantisce che non esiste uno stato in cui entrambi gli utenti stampano nello stesso momento, il che è proprio ciò che vogliamo. Detto questo, il modello presenta anche notevoli semplificazioni: non permette ad esempio a nessun utente di stampare due volte di fila.
Andiamo quindi a presentare una versione semplificata dell'algoritmo di Peterson per la sincronizzazione di processi.
3.2.1 Algoritmo di Peterson
L'algoritmo di Peterson è un esempio di algoritmo che permette di gestire una risorsa, come una stampante, tramite un accesso mutualmente esclusivo, nel senso che in un dato momento un solo utente ha accesso alla risorsa, mentre gli altri devono aspettare.
Adesso i due utenti condividono le seguenti tre variabili:
Una variabile \(r_a\) (r per "richiesta") che l'utente \(A\) imposta a true per indicare che vuole stampare. Inizialmente \(r_a\) è settata a false.
Una variabile \(r_b\) che è l'angolo di \(r_a\) ma per l'utente \(B\).
Una variabile \(\text{turn}\) che viene utilizzata per gestire i conflitti
L'automa che modella il comportamento dell'utente \(A\) è mostrato a seguire e l'automa per \(B\) è simmetirco, basta cambiare \(A\) con \(B\).
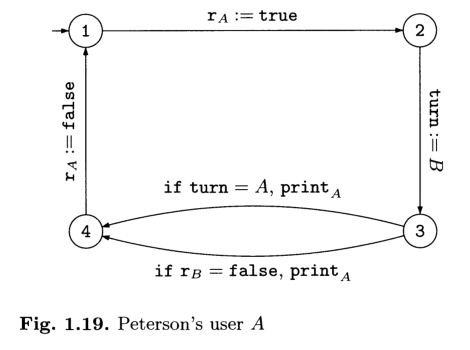
L'automa che rappresenta l'intero sistema è quindi ottenuto da questi due automi e dalle tree variabili condivise \(r_a\), \(r_b\) e \(\text{turn}\). Questo significa che uno stato globale del sistema è formato dai seguenti cinque componenti:
Lo stato dell'automa per \(A\)
Lo stato dell'automa per \(B\)
Il valore di \(r_a\)
Il valore di \(r_b\)
Il valore di \(\text{turn}\)
Notiamo che anche se questo automa teoricamente ha \(4 \cdot 4 \cdot 2 \cdot 2 \cdot 2 = 128\) stati, in realtà il numero di stati realmente raggiungibili è solamente \(21\). È possibile dimostrare che nessun stato della forma \((4, 4, \text{-}, \text{-})\) è raggiungibile, ovvero che non esiste uno stato in cui entrambi gli utenti stampano.