MVS - 09 - Model Checking in PLTL
Lecture Info
Date:
In questa lezione abbiamo visto come trattare il problema del model checking quando ci restringiamo a formule in PLTL.
1 Extended Regex
In PLTL la P sta per "propositional", ovvero al fatto che non ci sono i quantificatori e si parla solamente di cammini. In questo contesto quindi è possibile parlare "localmente" di un cammino. Avrò poi un unico quantificatore \(A\) sullo stato iniziale per dar senso al concetto di verifica.
Il vantaggio di PLTL è che sul singolo cammino posso combinare gli operatori temporali in qualsiasi modo, e posso quindi verificare proprietà del tipo
\[F^{\infty}(P) := G(F(P))\]
Notiamo che i cammini che soddisfano la formula precedente hanno hanno la seguente formula
\[\underbrace{\neg P, \neg P, \neg P, \ldots, P}_{(\neg P)^*P \text{ pattern}}, \underbrace{\neg P, \neg P, \neg P, \ldots, P}_{(\neg P)^*P \text{ pattern}}, \ldots\]
Espressioni come \((\neg P)^*P\) sono riprese dalla teoria dei linguaggi, e sono chiamate espressioni regolari. In realtà le espressioni che utilizzeremo noi sono una estesione delle espressioni regolari al caso in cui possiamo avere anche una sequenza numerabile di simboli.
Per passare dalla sequenze finite (trattate dalle tipiche espressioni regolari), alle sequenze infinite, si introduce un nuovo simbolo \(\omega\) con il significato := "si ripete un numero numerabile di volte". In totale troviamo quindi la seguente espressione regolare generalizzata
\[((\neg P)^* P)^{\omega}\]
Se invece voglio definire una sequenza che contiene almeno un \(\neg P\) allora devo scrivere un qualcosa di simile alla seguente formula
\[(F^{\infty} (P)) \land (F (\neg P))\]
e trasformandolo in espressione regolare estesa si ottiene
\[(P + (\neg P))^* (\neg P) ((\neg P)^* P)^{\omega}\]
2 Model Checking in PLTL
Il model checking in PLTL si basa sulla possibilità di associare ad ogni PLTL formula \(\phi\) una espressione \(\omega\) -regolare \(\mathcal{E}_\phi\) che descrive la forma imposta alle esecuzioni che soddisfano \(\phi\). Una volta fatto verificare se l'automa soddisfa la formula si riduce a verificare se le esecuzioni prodotte dall'automa verificano la forma descritta dall'espressione \(\mathcal{E}_\phi\).
In pratica l'algoritmo di verifica non lavora sulle espressioni regolari in modo diretto, ma su un particolare automa. Data la formula \(\phi\), l'algoritmo di verifica si costruire l'automa \(\mathcal{B}_{\neg \phi}\) che accetta esattamente le esecuzioni che non soddisfano la formula \(\phi\). Il size dell'automa creato, nel caso peggiore, è \(O(2^{|\phi|})\).
Una volta costruito \(\mathcal{B}_{\neg \phi}\), l'idea è quella di sincronizzare l'automa con \(\mathcal{A}\) per ottenere un nuovo automa, denotato con \(\mathcal{A} \mathbin{\otimes} \mathcal{B}_{\neg \phi}\), il cui comportamento è formato dalle esecuzioni di \(\mathcal{A}\) che vengono accettate da \(\mathcal{B}_{\neg \phi}\).
Il problema della verifica "\(\mathcal{A} \models \phi\)?" si riduce quindi al seguente: "il linguaggio riconosciuto dall'atuoma \(\mathcal{A} \otimes \mathcal{B}_{\neg \phi}\) è vuoto oppure no?"
2.1 Example
Consideriamo la seguente formula PLTL
\[\phi := G(P \implies X F Q)\]
Come prima cosa l'algoritmo di verifica si costruire l'automa delle esecuzioni che non soddisfano \(\phi\). In altre parole, mi costruisco l'automa che accetta \(\neg \phi\). Ora, dato che
\[\begin{split} \neg \phi &= F \neg (P \implies XFQ) \\ &= F (P \land \neg XFQ) \\ &= \ldots \\ &= F (P \land G(\neg Q)) \\ \end{split}\]
detto in altre parole abbiamo che \(\neg \phi\) equivale a dire che esiste una occorrenza di \(P\) dopo la quale non incontreremo mai un \(Q\). Troviamo quindi il seguente automa
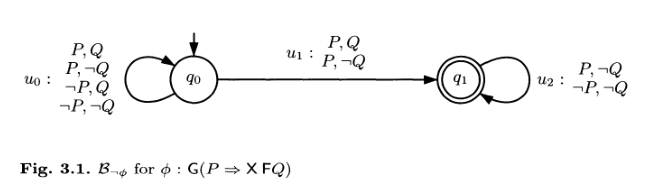
A questo punto consideriamo il seguente automa \(\mathcal{A}\) che vogliamo verificare
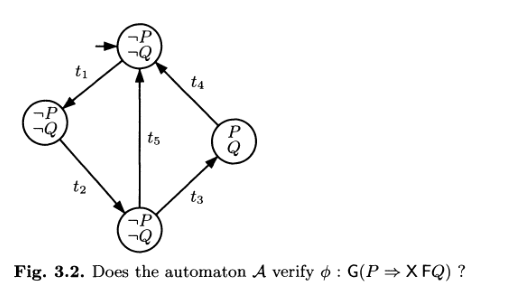
Per capire se l'automa \(\mathcal{A}\) verifica la formula \(\phi\) dobbiamo sincronizzare i due automi, cosa che può essere fatta come segue
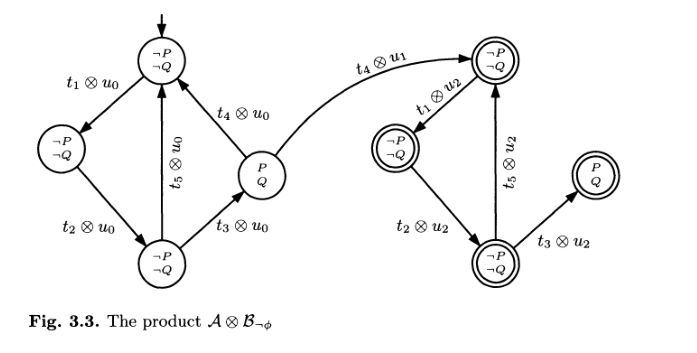
La sincronizzazione deve tener conto del fatto che le transizioni di \(\mathcal{B}_{\neg \phi}\) sono etichettate con gli stati di \(\mathcal{A}\).
2.2 Theory of infinite automata
Cosa vuol dire automa a stati finiti accetta una stringa di lunghezza infinita? L'idea è che accetta se e solo se entra infinite volte in uno stato accettante. Se la stringa è finita invece deve finire in uno stato accettante.
Osservazione: gli automi che modellano sistemi non hanno stati accettanti, mentre quelli che verificano proprietà hanno degli stati accettanti.
Nella trattazine precedente abbiamo tralasciato i dettagli tecnici relativi alla costruzione automatica dell'automa \(\mathcal{B}_{\neg \phi}\). Dal punto di vista della complessità, gli aspetti importanti della costruzione sono i seguenti:
\(\mathcal{B}_{\neg \phi}\) ha un size \(O(2^{|\phi|}\) nel caso peggiore;
Il prodotto tra automi \(\mathcal{A} \otimes \mathcal{B}_{\neg \phi}\) ha size \(O(|\mathcal{A}| \times \mathcal{B}_{\neg \phi})\);
Se l'automa sincronizzato è contenuto interamente in memoria, possiamo determinare se accetta un linguaggio non vuoto in tempo proporzionale al più alla cardinalità dell'automa, ovvero \(O(|\mathcal{A} \otimes \mathcal{B}_{\neg \phi}|)\).
3 The State Explosion Problem
Il più grande ostacolo incontrato dagli algoritmi di verifica automatica prende il nome di state explosion problem.
Sia per quanto riguarda il model checking nell'ambito più generale della CTL, sia per quanto riguarda il contesto più ristretto delle formule PLTL, in entrambi i casi l'algoritmo si basa sulla costruzione esplicita dell'automa \(\mathcal{A}\) che deve essere verificato. A seconda del particolare contesto poi possiamo muoverci in direzioni diverse:
Nel caso delle CTL, abbiamo delle procedure di marking che esplorano l'insieme degli stati raggiungibili da \(\mathcal{A}\), ottenuti tramite una reachability analysis.
Nel caso del PLTL invece, dobbiamo calcolare la sincronizzazione di \(\mathcal{A}\) con \(\mathcal{B}_{\neg \phi}\).
In pratica però il numero di stati dell'automa \(\mathcal{A}\) tende ad esplodere molto velocemente. In particolare tipicamente tende ad essere esponenziale rispetto alla descrizione del sistema.
Notiamo poi che quando il sistema che stiamo modellando deve considerare valori che non hanno un bound a priori, allora lo possiamo modellare solamente con un automa con un infinito numero di stati, e i metodi qui descritti non funzionano più.