WMR 02 - Maching Learning Methods
Date:
Course Site: Web Mining e Retrieval (a.a. 2019/20)
Lecturer: Roberto Basili
Slides: (wmr_02.pdf)
Table of Contents:
In questa lezione introduciamo la natura dell'apprendimento automatico con alcuni punti di vista del machine learning ispirati alla teoria statistica dell'apprendimento.
Il ML è una disciplina che fa parte dell'intelligenza artificiale e si basa sullo sfruttamento dei dati a disposizione al fine di automatizzare la risoluzione di problemi complessi.
Dal punto di vista algebrico, fare apprendimento significa utilizzare i dati per ottenere una rappresentazione funzionale utile che ci permette di generalizzare i dati.
I due problemi di riferimento nel machine learning sono i seguenti:
Classificazione
Regressione
Anche se i problemi di classificazione e regressione utilizzano delle funzioni di ottimizzazioni diverse, in entrambi i casi abbiamo degli aspetti in comune, che sono:
Forte dipendenza dalla rappresentazione del problema.
Capacità di valutazione dell'ottimalità del modello. L'ottimalità in questo caso consiste nel cercare di riprodurre nel modo più fedele possibile le tendenze che sono state viste nel passato.
Andiamo a vedere in modo più dettagliato le due tipologie di problemi.
La classificazione (classification) consiste nel definire l'appartenenza o meno di un insieme di punti ad una determinata classe (concetto). Consideriamo il seguente esempio di classificazione
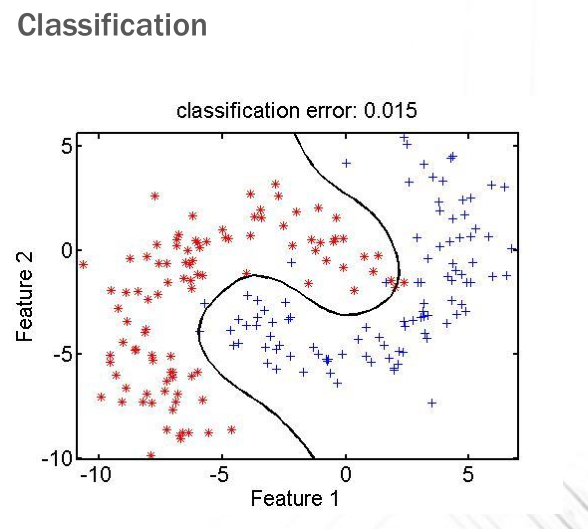
Risolvere il problema di classificazione mostrato significa definire una funzione che idealmente divide il piano in due porzioni: il semipiano composto dei punti che si trovano a sinistra della funzione e che appartengono al concetto e il semipiano composto dai punti che si trovano a destra della funzione e che non appartengono al concetto.
Funzionalmente parlando quindi, "apprendere un concetto" significa apprendere la funzione caratteristica che mappa i punti del dominio in analisi nell'insieme \(\{0,1\}\) e che mi dice quali sono le istanze che appartengono al concetto e quali sono quelle che non appartengono al concetto.
L'esperienza in questo caso è composta dai punti, che possono essere rossi, ovvero possono appartenere al concetto (di essere rosso), oppure blu, ovvero non appartenere al concetto. Tramite questi punti possiamo quindi costruirci il nostro modello di classificazione, che in questo caso è una legge di discriminazione tra due porzioni del piano ed è una funzione dell'esperienza.
Una volta definito un modello, lo possiamo applicare ai nostri dati. Per capire le performance del nostro modello dobbiamo calcolare i falsi positivi e i falsi negativi. Nel caso dell'esempio mostrato precedente abbiamo che
Falsi positivi: punti blu, che non appartengono al concetto ma che erroneamente si trovano a sinistra della funzione, e quindi secondo il nostro modello appartengono al concetto.
Falsi negativi: punti rossi, che dovrebbero appartenenre al concetto, che erroneamente vengono classificati dal nostro modello come non appartenenti al concetto.
Possiamo formalizzare il problema della classificazione come segue:
Classification: Date \(n\) classi \(C_1, C_2, \ldots, C_n\), ciascuna delle quali rappresenta un particolare concetto da apprendere, e dato un insieme di punti \(x_1, \ldots, x_k\) di cui la classificazione è nota, vogliamo definire una funzione di separazione \(h()\) tale che
\(h(x_i) = y_i\), dove \(y_i\) è la classe di appartenenza di \(x_i\), per ogni \(i=1,\ldots,k\).
Per tutti gli altri punti invece, se \(x \in C_i\), allora per definizione vogliamo \(h(x) = C_i\).
In altre parole, la nostra funzione \(h()\) deve dividere i punto in modo corretto tra le varie classi.
In alcuni casi è possibile dividere il piano utilizzando una semplice retta
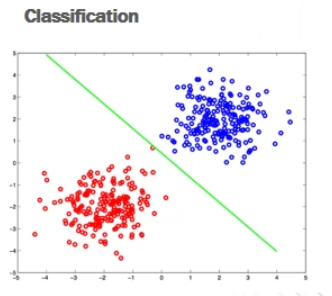
Molto spesso però è necessario utilizzare delle leggi più complesse.
Un problema di regressione è un problema in cui ho una conoscenza limitata di una funzione. Possiamo ad esempio pensare di avere una funzione composta da una variabile indipendente e una variabile dipendente. I valori della variabile dipendente sono noti solo per un sottoinsieme specifico di valori della variabile indipendente.
Risolvere il problema in questo caso significa apprendere la funzione a noi ignota, ovvero capire la relazione che lega la variabile dipendente a quella indipendente. Dato che la variabile indipendente si muove in uno spazio continuo, fare regressione significa estendere la conoscenza dei punti noti a tutti i punti del dominio.
Consideriamo il seguente esempio di regressione
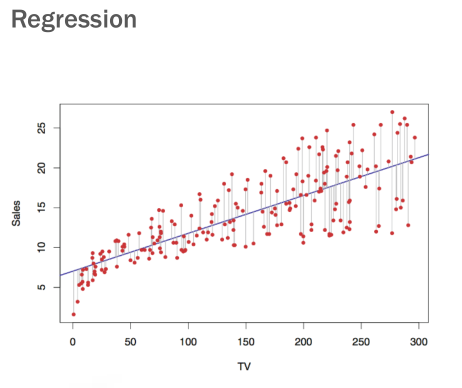
In questo caso l'esperienza ci è data dai punti rossi, che sono le coppie di valori \((\text{TV}, \text{Sales})\), e la funzione di regressione è quella funzione che cerca di avvicinarsi il più possibile a tutti i punti noti.
Possiamo formalizzare il problema della regressione come segue.
Regression: Dato un insieme di esempi \((x_i, t_i)\) di una funzione target \(f()\) non nota, vogliamo definire una funzione \(h()\) tale che:
\(h(x_i) = t_i = f(x_i)\) per ogni \(i = 1,\ldots,k\).
\(h(x) \approx f(x)\) per tutti gli altri punti \(x\).
A seconda della funzione \(f()\) possiamo scegliere la particolare forma della funzione \(h()\) che vogliamo utilizzare per approssimare \(f()\). A seconda della forma della funzione \(h()\) avremo più o menoo gradi di libertà tramite i quali possiamo modellare \(h()\) per renderla la migliore approssimazione di \(f()\). Ad esempio, se \(h()\) è un polinomio, possiamo scegliere il grado di \(h()\).
I seguenti esempi fanno vedere che nel caso in cui \(h()\) è un polinomio, aumentando il grado di \(h()\) (linea rossa) siamo in grado di approssimare meglio la funzione \(f()\) (linea verde).
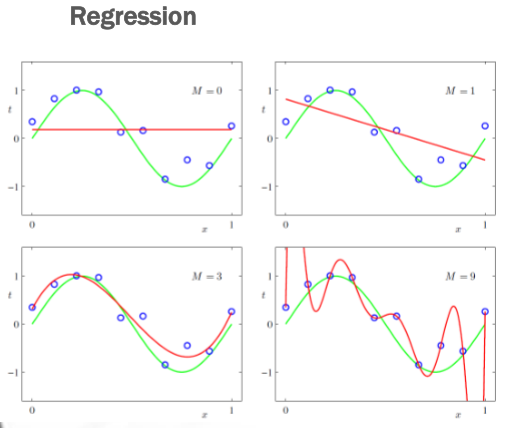
Notiamo però che ad un certo punto aumentare il grado di \(h()\) non solo non migliora più l'approssimazione ottenuta, ma la peggiora. In questo caso infatti ci siamo conformati troppo all'esperienza data, e non siamo più in grado di predirre i dati al di fuori di quelli noti dall'esperienza passata. Questo fenomeno è chiamato overfitting.
Viceversa, l'underfitting è definito come l'incapacità di adeguarsi adeguatamente all'esperienza pregressa.
Sia per il problema della regressione che il problema della classificazione, il punto di partenza è sempre la distribuzione dei dati in input. A partire da questi, siamo interessati a definire dei modelli (funzioni), che minimizzano l'errore. Aumentando la complessità delle funzioni considerate, siamo in grado di diminuire sempre di più l'errore. Ad un certo punto però questa tendenza si inverte, si va in overfitting, e l'errore diminuito sui dati di training è un miglioramento solo apparente, in quanto il modello risultante non è più utile per predirre i dati al di fuori dei dati di training.
La scelta della famiglia delle funzioni considerate e di come parametrizzarla fa parte del processo di selezione del modello che prende il nome di model selection. Selezionare un modello significa selezionare la funzione \(h()\) ottima. Questo processo può essere diviso nelle seguenti due sotto-scelte:
Model Family Selection: Scelta della classe di funzioni che andiamo a considerare. Un possibile esempio sono i polinomi di grado \(n\).
Model Parametrization: Scelta di come calcolo (tipicamente tramite delle stime) i parametri del modello scelto precedentemente per trovare la funzione più ottimale all'interno della famiglia. Questo dipende dai criteri di ottimalità utilizzati, che tipicamente sono l'accuracy e la coverage.
Aumentare l'accuracy significa volere un modello che si esprime in modo molto fedele rispetto alla vera natura del fenomeno studiato. Il costo di avere una elevata accuracy è che certe volte può succedere che il modello decide di non rispondere rispetto a determinate istanze al fine di preservare l'accuratezza, andando quindi ad aumentare il numero di falsi negativi.
Aumentare la coverage invece consiste nell'aumentare il numero di volte in cui il modello si esprime in modo corretto. Il costo di avere una elevata accuracy è il fatto che, dovendo sempre decidere, il modello certe volte potrebbe decidere in modo sbagliato e introdurre dei falsi positivi.
Dato un criterio di ottimizzazione, che può essere basato sui concetti di accuracy e coverage, si attiva un processo di ricerca della funzione che massimizza tale criterio. Questo processo di ricerca può avvenire in due modi:
In modo analitico, per tutti quei problemi che hanno delle soluzioni in forma chiusa. Il metodo di Netwon è un esempio di questo tipo di ricerca analitica e ci permette di approssimare gli zeri di una funzione. Nel corso vedremo le support vector machines.
Campionamento ricorrente del training set per vedere il problema da più punti diversi e infine scegliere la funzione che in media è la migliore. Nel corso vedremo i metodi neurali, che fanno cose del genere.
Andiamo adesso a vedere due diverse famiglie di funzioni: una algebrica/geometrica e l'altra statistica/probabilistica.
Utilizzando dei modelli lineari possiamo definire delle rette della forma \(\mathbf{w} x + b\) che ci permettono di separare il piano per classificare le istanze. La funzione di classificazione diventa quindi
\[h(x) = \text{sign}(\mathbf{w} x + b)\]
Il vettore \(\mathbf{w}\) è detto gradiente della retta, ed è il vettore che contiene le derivate parziali della funzione implicita utilizzata per descrivere la retta. Il valore \(b\) invece è detto termine noto, e ci dice come la retta si muove rispetto all'origine.
Esempio: Nel piano in due dimensioni possiamo descrivere una retta in modo implicito tramite la seguente equazione
\[ax + by + c = 0\]
Il gradiente è quindi \(\mathbf{W} = (a, b)\) e il termine noto è \(c\).
Consideriamo adesso la seguente immagine, che mostra quattro possibili modelli lineari per classificare le istanze
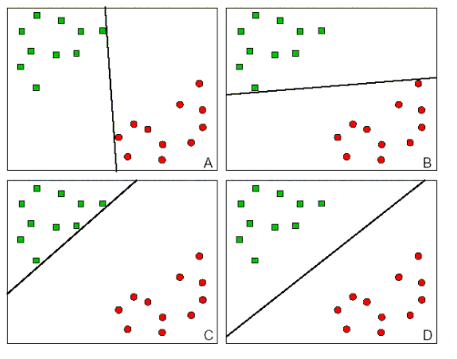
Notiamo che in tutti e quattro i casi l'utilizzo del modello lineare ci permette di dividere perfettamente il training set.
La differenza tra queste rette è che, ad esempio, mentre le rette \(A\) e \(B\) sono pericolosamente vicine a determinati punti verdi e rossi, le rette \(C\) e \(D\) sono più equilibrate in questo. Notiamo poi come la retta \(C\) è molto prudente nel decidere chi fa parte del concetto, e dunque tenderà ad aumentare l'accuracy a costo della coverage. La retta \(D\) invece è quella che riesce a trovare il giusto bilanciamento tra accuracy e coverage.
Questa tipologia di modelli si basa quindi sulla distribuzione dei punti di training all'interno di uno spazio metrico.
I modelli probabilistici invece non si basano su uno spazio matrico, ma si basano sulla stima della pobabilità che una certa istanza \(x\) appartenga ad una certa classe \(C_k\), in formula \(P(C_k|x)\). L'idea di questi modelli è quindi quella di calcolare le varie probabilità
\[P(C_1 | x), \;\; P(C_2 | x), \ldots, P(C_n | x)\]
per poi assegnare all'istanza \(x\) la classe che massimizza tale probabilità.
Al fine di calcolare queste probabilità possono essere utilizzate le solite leggi della probabilità e i soliti approcci statistici. Una legge estremamente utile in questo contesto risulta essere la regola di Bayes, che ci dice ceh
\[P(C_k | x) = \frac{P(x | C_k) \cdot P(C_k)}{P(x)}\]
La legge di Bayes infatti ci permette di utilizzare l'esperienza passate per calcolare o stimare le probabilità a cui siamo interessati.
Esistono vari modelli probabilistici, tra cui troviamo anche i seguenti:
Le probabilità possono essere utilizzate anche in modo più strutturato. Infatti, se ho degli eventi \(A, B, C, D, E\) e se suppongo di conoscere la struttura delle dipendenze tra i vari eventi tramite il seguente grafo,
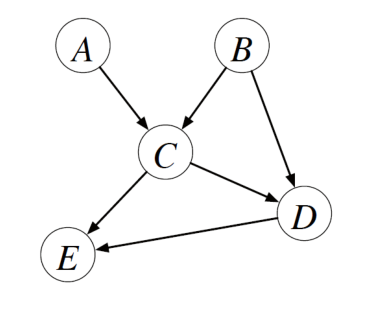
posso calcolarmi la probabilità degli eventi congiunti \(A, B, C, D, E\) come prodotto delle seguenti probabilità
\[P(A) \cdot P(B) \cdot P(C | A, B) \cdot P(D | B, C) \cdot P(E | C, D)\]
Questi grafi che codificano in modo grafico le relazioni di dipendenza tra le variabili aleatorie vengono chiamati modelli grafici e ci permettono di considerare solo un sottinsieme delle distribuzioni di probabilità.
Nell'esempio visto prima, possiamo dire che l'evento \(E\) è generato dagli eventi \(A, B\), in quanto sono gli eventi \(A\) e \(B\) che generano gli eventi \(C\) e \(D\), che a loro volta generano l'evento \(E\).
Alcuni modelli generativi interessanti sono quelli in cui le distribuzioni nel continuo vengono combinate per generare distribuzioni più puntuali.
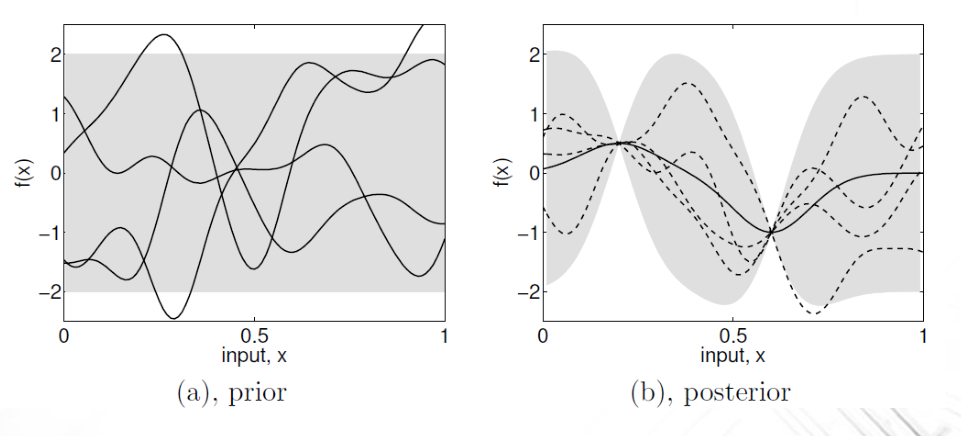
In questo caso possiamo pensare che la forma d'onda dell'output è ottenuta come combinazione lineare di forme d'onda che rappresentano fenomeni differenti.
Un ambito in cui molto spesso i modelli probabilistici vengono utilizzati è quello del processamento del linguaggio naturale.
Le Probabilistic Context-Free Grammars (pCFGs) cercano di combinare l'idea teorica di utilizzare una grammatica CF per modellare il linguaggio assieme all'idea statistica del fatto che certe produzioni linguistiche sono più probabili di altre.
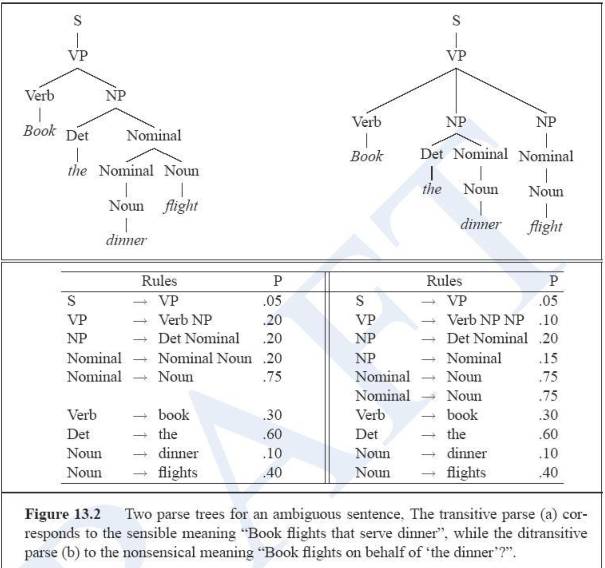
Tramite l'utilizzo delle pCFGS siamo in grado di eliminare l'ambiguità sintattica andando a scegliere l'albero sintattico che massimizza la sua probabilità.
Un altro modello generativo famoso prende il nome di Hidden Markov Model
Il modello di markov nascosto si basa sulla possibilità di osservare una sequenza di eventi \(Y_1, Y_2, \ldots, Y_t\) a causa di un insieme di stati non osservabili \(X_1, X_2, ..., X_t\). In particolare si ha che lo stato \(X_i\) giustifica l'osservazione dell'evento \(Y_i\).
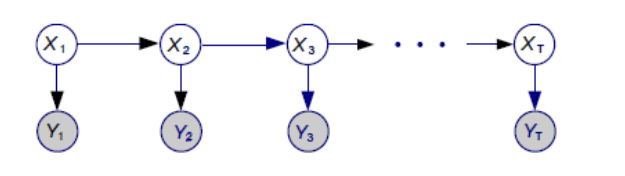
Notiamo che gli stati che hanno generato gli eventi osservabili non sono scorrelati tra loro. In particolare negli hidden markov models assumo che ciascun stato \(X_i\) può dipendere solamente dal precedente \(X_{i-1}\). Questa assunzione dà un limite alla complessità del modello, ma ci permette di effettuare dei calcoli interessanti. La probabilità di avere la sequenza \(X_1, \ldots, X_t, Y_1, \ldots, Y_t\) di stati interni (non osservabili) e di eventi osservati è pari a
\[ p(X_1) \cdot P(Y_1 | X_1) \cdot \prod_{i = 2}^t P(X_t | X_{i-1}) \cdot P(Y_i | X_i) \]
Se si utilizza una catena di markov nascota per formalizzare il nostro problema, risolverlo significa scoprire la sequenza degli stati nascosti \(X_1,...X_t\). Per fare questo bisogna prendere l'equazione precedente e trovare gli stati \(X_1,...,X_t\) che massimizzano tale probabilità.
Molti task linguistici possono essere tradotti in un problema di decodifica di una HMM, che consiste nel trovare la sequenza di stati \(X_1, \ldots, X_t\) più probabile che è alla base degli eventi osservati \(Y_1, \ldots, Y_t\). Qualche esempio:
Speech recognition: In questo contesto possiamo modellare un segnale audio continui in segmenti, ciascuno dei quali rappresenta il segnale audio di una particolare parola, e modellare il tutto con un HMM.
Part Of Speech tagging: In questo caso gli eventi osservabili sono le parole e gli stati nascosti sono le categorie del discorso (nome, verbo, aggettivo) delle varie parole.
Nel corso di questa lezione abbiamo visto che il machine learning è caratterizzato dalle seguenti cose:
Mappatura di un problema in un dominio.
Scelta di una famiglia di funzione all'interno del dominio in cui si è andato a mappare il problema per fare regressione o classificazione.
Parametrizzazione delle funzioni all'interno delle famiglie scelte, a seconda del problema da risolvere.