WMR 03 - Geometrical Models I
Date:
Course Site: Web Mining e Retrieval (a.a. 2019/20)
Lecturer: Roberto Basili
Slides: (wmr_03.pdf)
Table of Contents:
Questa lezione è stata divisa in due parti:
Nella prima parte, svolta in live su microsoft teams, è stato introdotto il modello dello spazio vettoriale.
Nella seconda parte, svolta tramite una videolezione, sono stati introdotti i primi modelli geometrici utilizzati nel contesto della text classification.
Uno spazio vettoriale è insieme di oggetti chiamati vettori. Un vettore \(\underline{x}\) è formato da una sequenza di valori, chiamati scalari, che vengono presi da un particolare insieme. Per rappresentare gli scalari che formano un vettore si utilizza la seguente notazione
\[ \underline{x} = \begin{pmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{pmatrix} \]
Da un punto di vista formale uno spazio vettoriale \(V\) su un certo insieme di scalare \(W\) è definito come un insieme con due operazioni: la somma vettoriale \((+)\) e la moltiplicazione per uno scalare \((\cdot)\). Ciascuna operazione deve rispettare una serie di proprietà. La somma in particolare deve rispettare le seguenti:
La somma è commutativa:
\[\forall x, y \in V: \,\, x + y = y + x \]
La somma è associativa:
\[\forall x, y, z \in V: \,\, x + (y + z) = (x + y) + z \]
Esiste un elemento neutro per la somma, denotato con \(\phi\), tale che
\[\forall x \in V: \,\, x + \phi = x\]
Per ogni elemento \(x \in V\) esiste un elemento opposto ad \(x\), denotato \(-x\), tale che
\[x + (-x) = \phi\]
Siano \(\alpha\) e \(\beta\) due scalari presi dall'insieme \(W\) e siano \(\underline{x}\), \(\underline{y}\) due vettori presi da \(V\). L'operazione di moltiplicazione per uno scalare deve rispettare le seguenti proprietà:
\(\alpha \cdot (\beta \cdot \underline{x}) = (\alpha \cdot \beta) \cdot \underline{x}\)
\(1 \cdot \underline{x} = \underline{x}\)
\(\alpha \cdot (\underline{x} + \underline{y}) = \alpha \cdot \underline{x} + \alpha \cdot \underline{y}\)
\((\alpha + \beta) \cdot \underline{x} = \alpha \cdot \underline{x} + \beta \cdot \underline{x}\)
Siano \(\underline{x}, \underline{y}\) due vettori e sia \(\alpha\) uno scalare. Un possibile modo di definire delle operazioni che rispettano le proprietà menzionate prima è il seguente:
Somma: L'idea è quella di sommare gli scalari due vari vettori per ottenere il vettore somma. In formula,
\[ \underline{x} + \underline{y} := \begin{pmatrix} x_1 + y_1 \\ x_2 + y_2 \\ \vdots \\ x_n + y_n \end{pmatrix}\]
Moltiplicazione per scalare: L'idea è quella di moltiplicare lo scalare per i vari scalari che formano il vettore \(\underline{x}\). In formula,
\[ \alpha \cdot \underline{x} := \begin{pmatrix} \alpha \cdot x_1 \\ \alpha \cdot x_2 \\ \vdots \\ \alpha \cdot x_n \end{pmatrix} \]
Notiamo come le operazioni appena definite riflettono il risultato delle operazioni tra i vari scalari al risultato generale tra i due vettori.
Osservazione: Con la notazione \(:=\) stiamo indicando che stiamo parlando di una definizione, ovvero che ciò che si trova alla sinistra di dell'uguale sta "prendendo significato" utilizzando ciò che si trova alla destra dell'uguale.
Utilizzando le operazioni di somma e moltiplicazione per uno scalare possiamo introdurre il concetto di combinazione lineare. Una combinazione lineare è una espressione della forma
\[c_1 \cdot \underline{x}_1 + c_2 \cdot \underline{x}_2 + ... + c_n \cdot \underline{x}_n\]
dove \(c_1, ..., c_n\) sono scalari e \(\underline{x}_1, ..., \underline{x}_n\) sono vettori.
Un insieme di vettori \(\{\underline{x}_1, \underline{x}_2, ..., \underline{x}_n\}\) è detto linearmente dipendente se esiste una combinazione lineare con gli scalari \(c_1, c_2, ..., c_n\) non tutti nulli, tale che
\[c_1 \cdot \underline{x}_1 + c_2 \cdot \underline{x}_2 + ... + c_n \cdot \underline{x}_n = 0\]
Se questo non è possibile, ovvero se tutte le combinazioni lineari nulle hanno tutti i coefficienti nulli, allora i vettori si dicono linearmente indipendenti.
Una base per uno spazio vettoriale è un insieme di \(n\) vettori linearmente indipendenti in uno spazio \(n\) dimensionale.
Fissata una base \(\mathcal{B}\) per uno spazio vettoriale \(V\), possiamo esprimere un vettore \(\underline{x} \in V\) come una combinazione lineare dei vettori della base. Così facendo siamo in grado di specificare un punto \(\underline{x}\) nello spazio utilizzando solamente i coefficienti \(c_1, c_2, ..., c_n\) della combinazione lineare di \(\underline{x}\) utilizzando i vettori della base \(\mathcal{B}\).
Il prodotto scalare, anche chiamato inner product o dot product, è una operazione definita su due vettori \(\underline{x}, \underline{y}\). Viene tipicamente denotata con la parantesi tonda \((x, y)\) e deve rispettare le seguenti proprietà:
\((x, y) = (y, x)\)
\((x, \lambda \cdot y) = \lambda \cdot (x, y)\)
\((x_1 + x_2, y) = (x_1, y) + (x_2, y)\)
\((x, x) >= 0\)
\((x, x) = 0 \iff x = 0\)
Il prodotto scalare "standard" che rispetta le proprietà menzionate è definito come il prodotto delle coordinate dei vettori. In formula,
\[(x, y) := \sum_{i = 1}^n x_i \cdot y_i\]
Utilizzando la notazione matriciale può anche essere scritto come
\[(x, y) = x^T \cdot y\]
dove con \(x^T\) si indica il vettore trasposto.
Osservazione: Notiamo come nella definizione data gli indici non si mischiano mai, e quindi le dimensioni agiscono in modo indipendente tra loro (or logico), mentre gli elementi con lo stesso indice invece si combinano tra loro (and logico) per ottenere il risultato finale.
È importante sottolineare il fatto che il particolare modo in cui abbiamo definito il prodotto scalare non è l'unico possibile. L'unica cosa che a noi importa è che, qualsiasi definizione diamo, essa deve dovrà rispettare le proprietà riportate per poter essere considerato un prodotto scalare.
Utilizzando il prodotto scalare possiamo ragionare sulla "grandezza", o "dimensione" dei vettori, che viene tipicamente chiamata norma. La norma è una funzione che va da uno spazio vettoriale \(V\) all'insieme dei vettori reali, \(|| \cdot || : V \to \mathbb{R}\) e tale che rispetta le seguenti proprietà
\(|| x || \geq 0\)
\(|| x || = 0 \iff x = 0\)
\(\forall \alpha \in W, x \in V: \,\,\, ||\alpha \cdot x || = |\alpha| \cdot || x ||\)
\(\forall x, y \in V: \,\, |(x, y)| \leq || x || \cdot || y ||\)
Osservazione: La diseguaglianza riportata come ultima proprietà da rispettare è chiamata Cauchy-Schwartz inequality.
Un vettore \(x\) è detto versore, o vettore unitario, se la sua norma è pari a \(1\), ovvero se \(|| x || = 1\).
Una delle norme più comuni è la norma euclidea, definita come la radice del prodotto scalare del vettore con se stesso. In formula,
\[ || x || := \sqrt{(x, x)} = \sqrt{\sum_{i = 1}^n x_i^2} = (x_1, ..., x_n)^{1/2} \]
In uno spazio vettoriale \(V\) possiamo anche definire il concetto di distanza. Una distanza è una funzione \(d(x, y): V \to \mathbb{R}\) che rispetta le seguenti proprietà:
\(d(x, y) \geq 0\)
\(d(x, y) = 0 \iff x = y\)
\(d(x, y) = d(y, x)\)
\(d(x, y) \leq d(x, z) + d(z, y)\)
Osservazione: La diseguaglianza riportata come ultima proprietà da rispettare è chiamata triangle inequality. La triangle inquality segue dalla cauchy-schwartz inequality.
Un possibile modo per definire la distanza tra due vettori è tramite l'utilizzo del concetto di norma introdotto prima. Infatti è possibile definire la distanza tra due vettori come la norma della loro differenza. In formula,
\[ d(x, y) := || x - y ||\]
Questo tipo di distanza è chiamata distanza euclidea ed è denotata con \(|| x - y ||_2^2\).
Un modo alternativo per calcolare il prodotto scalare definito prima è il seguente
\[ (x, y) = \sum_{i=1}^n x_i \cdot y_i = || x || \cdot || y || \cdot \cos(\phi)\]
dove \(0 \leq \phi \leq \pi\) è l'angolo tra i vettori \(x\) e \(y\).
Dato che molto spesso nel contesto del machine learning a noi interessa non tanto la norma dei vettori quando la loro direzione nello spazio, un'altra possibile definizione per la funzione distanza può essere introdotta introducendo quella che viene chiamata cosine distance, definita nel seguente modo
\[ \cos(\phi) = \frac{(x, y)}{ ||x|| \cdot ||y|| } \]
La cosine distance, dandoci una misura della distanza rispetto la direzione dei vettori, riesce in qualche modo a misurare la "somiglianza" tra due vettori in uno spazio vettoriale, ed è per questo molto utilizzata nel contesto dell'apprendimento automatico.
Osservazione: Se i vettori \(x\) e \(y\) sono unitari, il loro prodotto scalare corrisponde esattamente alla cosine distance. Per questa ragione nel machine learning si tende molto a normalizzare i dati rappresentati in forma vettoriale, in modo da poter lavorare direttamente con il prodotto scalare.
Due vettori \(x\) e \(y\) sono detti ortogonali se e solo se il loro prodotto scalare è \(0\).
Un insieme di vettori linearmente indipendenti \(\{\underline{x}_1, \underline{x}_2, ..., \underline{x}_n \}\) in uno spazio \(V\) è chiamato una base ortonormale per lo spazio se e solo se:
\(\forall \underline{x}_i \in V\)
\[(\underline{x}_i, \underline{x}_i) = 1\]
\(\forall \underline{x}_i, \underline{x}_j \in V: i \neq j\)
\[(\underline{x}_i, \underline{x}_j) = 0\]
Andiamo adesso a vedere come gli spazi vettoriali sono utilizzati nel contesto dell'apprendimento automatico, e in particolare nel contesto della text classification, in italiano classificazione di documenti, in cui siamo interessati a capire, dato un documento, la classe, o le classi, a cui quel documento appartiene.
I documenti formano probabilmente la quantità maggiore di dati presenti nel web. Al fine di poter lavorare con grandi quantità di dati testuali, e in particolare al fine di poterli relazionale tra loro, inizialmente nell'ambito dell'information retrieval (IR) e successivamente anche in altri campi, si è deciso di procedere andando a mappare i documenti con dei vettori all'interno di spazi vettoriali. Questa scelta di rappresentazione è stata motivata dal fatto che uno spazio vettoriale è principalmente uno spazio metrico in cui è possibile definire e lavorare con i concetti di distanza e similarità tra vettori.
Un esempio di questa rappresentazione è data dal famoso Vector Space Model.
In questo modello le dimensioni dello spazio corrispondono alle parole del vocabolario. Ogni documento viene visto come un bag of words e viene mappato nello spazio vettoriale ad un vettore, ottenuto associando ad ogni parola del documento e quindi ad ogni coordinata del vettore, un particolare valore. Tipicamente il valore associato ad ogni parole è ottenuto pesando in qualche modo l'importanza della parola all'interno del documento, o più in generale all'interno del training set.
A seguire un esempio di spazio vettoriale costruito a partire da un vocabolario di due termini: "Cat" e "Mouse"
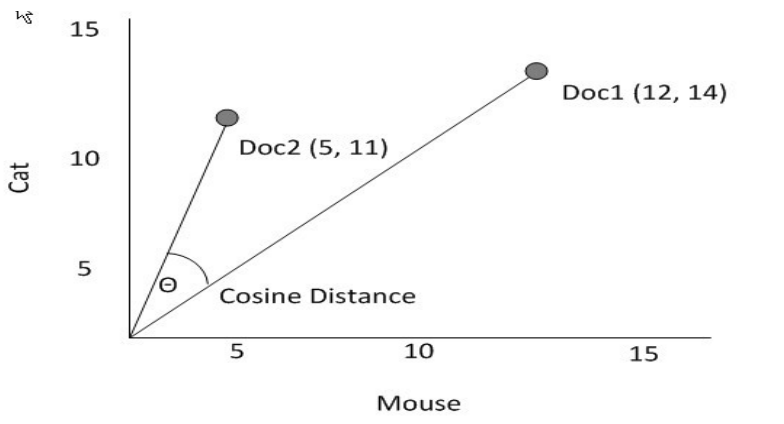
L'utilizzo del vector space model ci permette di avere una visione metrica del problema, e in particolare ci permette di stabilire la similarità di una copppia di documenti in funzione dell'angolo compreso tra i vettori che rappresentano i documenti nello spazio.
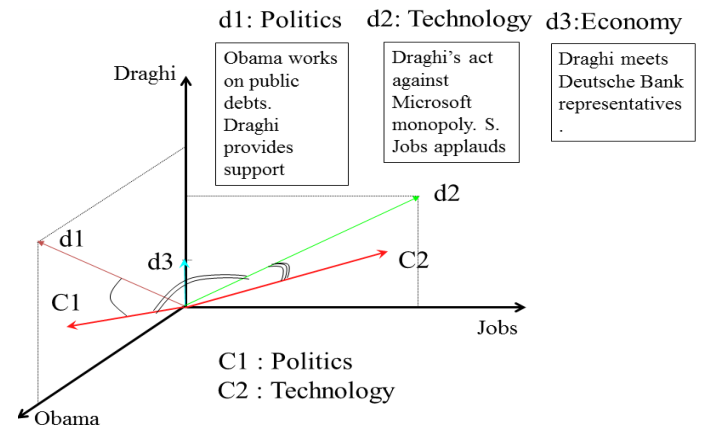
Più l'angolo tende ad essere piccolo, più i vettori sono allineati nella stessa direzione, e più possiamo pensare che i nostri documenti siano "simili" tra loro.
Osservazione: Per calcolare la "similarità" tra due documenti tipicamente si utilizza il coseno dell'angolo, in quanto il coseno di un angolo è massimizzato quando l'angolo è 0, mentre è minimizzato quando i due vettori sono ortogonali tra loro. Questo ci permette di avere una funzione che cresce al crescere della similarità tra due documenti.
Il task della text classification può essere formalizzato come segue
Text Classification: Date un insieme di categorie, \(C = \{C_1, ..., C_n\}\), e un insieme \(T\) di documenti, vogliamo definire una funzione \(f: T \to 2^C\) che associta ad ogni documento \(d \in T\) una o più categorie di \(C\), \(f(d) \subseteq C\).
A seconda di quello che possiamo utilizzare possiamo procedere con vari approcci. Ad esempio il problema del supervised text classification permette di avere a disposizione un insieme di documenti, detto training set, di cui sappiamo già le relative categorie per ogni documento. Se invece non abbiamo questo training set, allora il problema prende il nome unsupervised text classification, ed è tipicamente più difficile da risolvere.
Volendo utilizzare il vector space model per risolvere la classificazione dei testi, possiamo procedere mappando ogni documento \(d \in T\) e ogni categoria \(C_i \in C\) a dei vettori in uno spazio vettoriale. Le dimensioni dello spazio vettoriale utilizzato prendono il nome di features, mentre le coordiante dei vettori prendono il nome di features weights.
Con il vector space model la funzione \(f\) che fa il mapping tra documenti e categorie è definita in modo geometrico nel seguente modo: un documento \(d\) è assegnato ad una classe \(C_i\) se il prodotto scalare tra il vettore \(\underline{d}\) associato al documento \(d\) e il vettore \(\underline{C}_i\) associato alla classe \(C_i\) è maggiore di un certo valore \(\tau_i\), in formula
\[ C_i \in f(d) \iff (\underline{d}, \underline{C}_i) \geq \tau_i\]
Per utilizzare un vector space model dobbiamo quindi essere in grado di fare le due seguenti cose:
Calcolare il vettore \(\underline{d}\) per ogni documento \(d\).
Calcolare il vettore \(\underline{C}_i\) per ogni classe \(C_i\).
Il vettore \(\underline{C}_i\) che associamo alla classe \(C_i\) è proprio ciò che il nostro algoritmo di apprendimento deve imparare utilizzando l'esperienza passata, ovvero i dati di training.
L'algoritmo di Rocchio è uno dei primi e più semplici algoritmi che permettono di risolvere il task del supervised text classification tramite un vector space model, ed è composto dai seguenti elementi:
I vettori dei documenti vengono ottenuti tramite una funzione standard di pesatura che prende il nome di tf-idf.
I vettori delle categorie sono ottenuti facendo la media dei comportamento dei vettori presenti nel training set.
Per fare questo quindi si definisce una funzione di pesatura \(\omega(w, d)\) che calcola il peso che la parola \(w\) ha sul documento \(d\). Un esempio di questa funzione è la già citata tf-idf, che ci permette di ottenere una descrizione statistica dell'occorrenza della parola nel documento.
Una volta costruiti i vettori per i vari documenti e per le varie classi si procede calcolando la cosine similarity tra i vettori dei documenti e le varie classi. Al documento \(d\) assegno poi tutte le classi \(C_i\) per cui si ha che
\[(\underline{d} \;,\; \underline{C}_i) > \tau_i\]
La pesatura tf-idf, denotata da \(\omega(w, d)\), è calcolata combinando le due seguenti quantità
La term frequency (tf), che conta la numerosità della parola nel documento, ovvero il numero di volte in cui quella parola appare nel documento. Tipicamente questa quantità viene poi normalizzata per cercare di diminuire il più possibile l'impatto che la lunghezza del documento può avere sulla sua rappresentazione vettoriale. Dunque, se indichiamo con \(o_w^d\) il numero di occorrenze del termine \(w\) all'interno del documento \(d\), troviamo la seguente formula
\[tf_w^d = \frac{o_w^d}{\underset{x \in d}{\max} \,\, {o_x^d}}\]
La inverse document frequency (idf), il cui valore codifica quanto significativa la parola è nel documento. Indicato con \(N\) il numero totale di documenti e con \(N_w\) il numero di documenti che contengono la parola \(w\), abbiamo la seguente formula
\[idf_w^d = \log{\frac{N}{N_w}}\]
Tramite la idf, che dipende dall'intera collezione di documenti, possiamo:
Diminuire l'impatto delle parole comuni che vengono molto spesso utilizzate e che quindi si trovano in molti documenti, come il verbo essere.
Aumentare l'impatto delle parole rari che compaiono solo in un numero molto ristretto di documenti.
Tramite la funzione di pesatura tf-idf siamo in grado di costruire la rappresentazione vettoriale di ogni documento nel seguente modo
\[\underline{d}_i = \omega(w, d) = \big(tf_w^d \cdot idf_w^d\big)_{w \in W}\]
dove con \(W\) indichiamo il vocabolario delle parole preso in considerazione.
Al fine di costruire i vettori per le varie categorie procediamo definendo una funzione \(\Omega(w, C_i)\) che pesa il contributo della parola \(w\) nella categoria \(C_i\). Notiamo che il calcolo di questa funzione di pesatura necessariamente dovrà includere il training set utilizzato per fare addestramento supervisionato.
La funzione \(\Omega(w, C_i)\) è definita come segue,
\[\Omega(w, C_i) = \max\Bigg\{0, \;\;\; \frac{\beta}{|T_i|} \cdot \sum_{d \in T_i} \omega_w^d - \frac{\gamma}{|\overline{T}_i|} \cdot \sum_{d \in \overline{T}_i } \omega_w^d\Bigg\}\]
dove,
\(T_i\) è l'insieme dei documenti presenti nel training set e classificati come far parte della categoria \(C_i\)
\(\overline{T}_i\) è l'insieme dei documenti presenti nel training set che non fanno parte di \(C_i\).
La rappresentazione vettoriale della categoria \(C_i\) prende quindi il comportamento medio del peso dei termini contenuti nei documenti che fanno parte della categoria \(C_i\) e sottrae a questo il comportamento medio del peso dei termini contenuti nei documenti che non fanno parte della categoria \(C_i\).
I coefficienti \(\beta\) e \(\gamma\) sono dei fattori empirici che permettono di bilanciare il ruolo dei "positivi", ovvero delle parole che rappresentano la categoria \(C_i\), e dei "negativi", ovvero delle parole che non rappresentano la categoria \(C_i\). Se \(\gamma\) è vicino a 0 e \(\beta\) è molto più grande di 0, allora il modello visto prima è detto ottimista rispetto al training set, in quanto ci si tende a fidare dei pochi documenti classificati in \(C_i\) in cui la parola compare. Viceversa, se \(\beta\) è vicino a \(0\) e \(\gamma\) è molto più grande di \(0\), allora il modello è detto pessimista.
Una volta scelto il valore per i parametri \(\gamma\) e \(\beta\), possiamo costruire la rappresentazione vettoriale di ogni categoria. Tale vettore prende il nome di profilo di categoria ed è ottenuto nel seguente modo
\[\underline{C}_i = \begin{pmatrix} \Omega_1^i \\ \Omega_2^i \\ \vdots \\ \Omega_M^i \end{pmatrix}\]
Dove \(M\) è il size del vocabolario, e \(\Omega_j^i\) rappresenta il peso, calcolato con la formula prima, della \(j\) esima parola nel vocabolario.
A seguire una visione bidimensionale del modello di Rocchio, in cui i documenti di ciascuna categoria del training sono rappresentati da colori diversi. Notiamo che in questo esempio ciascun documento fa parte di una sola categoria, tra le due disponibili.
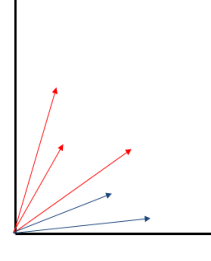
Andiamo adesso a calcolare i profili delle categorie estrapolando dal comportamento dei dati del training set
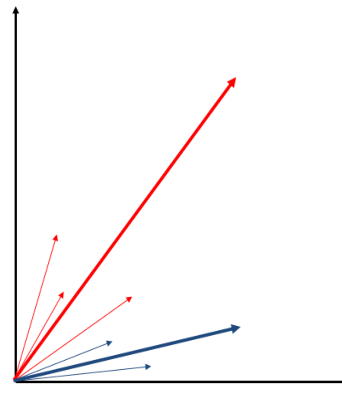
Adsso possiamo classificare una nuova istanza, rappresentata dal vettore colorato di verde, andandolo a confrontare con i profili delle categorie calcolati nel passo precedente
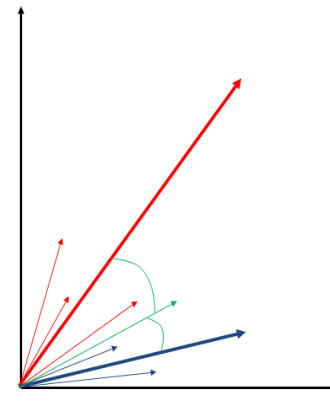
Dato che il nuovo documento minimizza l'angolo (e dunque massimizza la cosine similarity) rispetto al profilo della categoria blu, il documento sarà assegnato alla categoria blu.
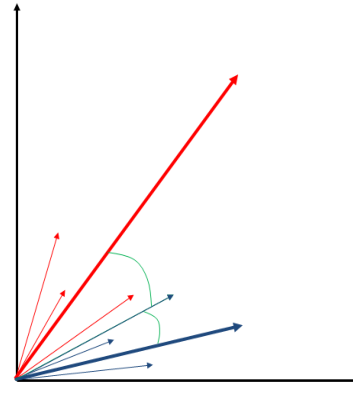
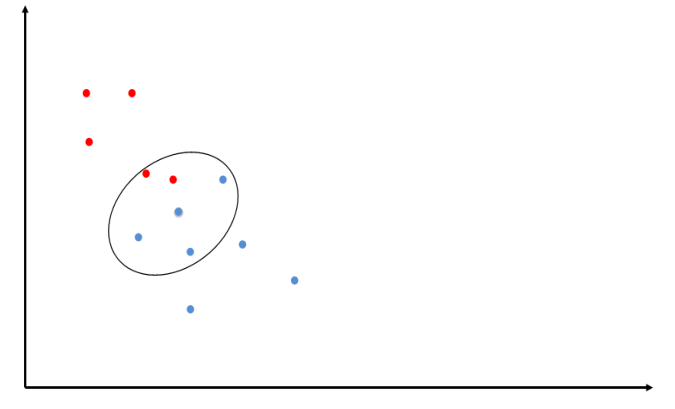
Anche se il modello di Rocchio funziona bene in molti casi, il calcolo della tendenza media effettuato dal modello di Rocchio non è molto utile quando abbiamo elementi molto eterogenei tra loro all'interno della stessa classe.
Infatti, il comportamento medio di comportamenti che solo localmente sono molto coesi ma che globalmente sono molto diversi da loro risulta essere poco rappresentativo dei singoli membri.
Un esempio di questo è mostrato nella seguente figura
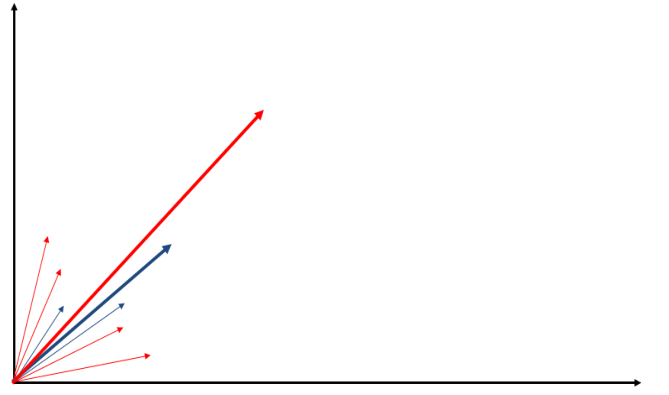
Un metodo empirico semplice e utile che possiamo utilizzare per risolvere il problema dell'algoritmo di Rocchio menzionato prima è chiamato Memory-based Learning.
Il memory based learning evita di definire un singolo profilo per ogni categoria e procede invece andando a memorizzare tutte le istanze di addestramento. Sia \(D\) il training set. Per assegnare una categoria ad una istanza \(x\) si procede nel seguente modo:
Si calcola la similarità tra \(x\) e tutti gli esempi contenuti in \(D\).
Si assegna a \(x\) la categoria dell'esempio più simile a \(x\) tra quelli contenuti in \(D\).
L'approccio utilizzato dal MBL, ovvero quello di non generalizzare dall'esperienza, ma piuttosto di utilizzarla così come è stata data è anche chiamato con i seguenti nomi alternativi:
Case-based
Memory-based
Lazy learning
Notiamo in ogni caso che la complessità del MBL sta nel calcolo della similarità descritto nel passo (1). Infatti, non generalizzando, il MBL si deve memorizzare ogni singola istanza di training per poi confrontarla con le istanze reali, e questo può essere costoso, sia in termini computazionali e sia in termini di spazio occupato.
L'implementazione più famosa del MBL è chiamata kNN, che sta per k-Nearest Neighborough.
Data una distrizuione di dati classificati (training set), supponiamo di dover classificare un nuovo punto nello spazio. L'idea è quella di inserire il punto nello spazio e calcolare i \(k\) punti già memorizzati più vicini al punto appena inserito. Il punto viene poi classificato in base alla categoria a cui fanno parte la maggior parte dei punti tra i \(k\) considerati.
Il fatto che il kNN utilizza gli esempi locali per effettuare la classificazione permette di risolvere il problema menzionato e presente nel modello di Rocchio.
Notiamo infine che \(k\) deve essere abbastanza grande ed è preferibile che sia un valore dispari per avere una netta maggioranza all'interno del gruppo di punti considerato.
A seguire un esempio grafico del kNN
Inseriamo il punto nello spazio, indicando come il cerchio colorato di bianco.
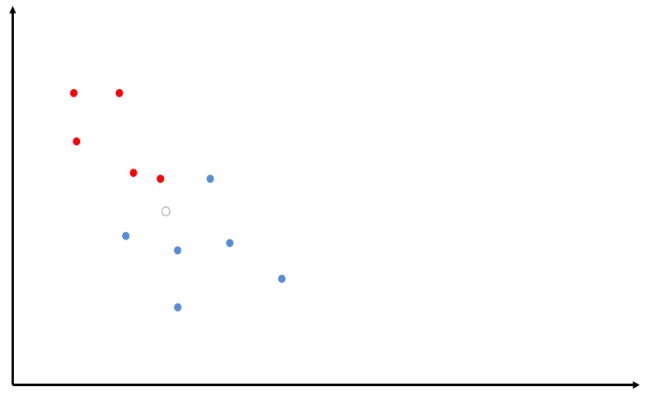
Calcoliamo adesso i \(k\) punti più vicini al punto dato e vediamo la categoria a cui appartengono la maggioranza dei punti. Dato che in questo caso la maggioranza di punti è blu, allora classifichiamo il punto come un punto blu.
Per ogni documento \(x\) del training set \(D\), il kNN si calcola la sua rappresentazione vettoriale utilizzando la pesatura tf-idf vista prima al fine di ottenere il vettore \(\underline{x}\).
Dato un nuovo documento \(y\) da classificare si procede poi nel seguente modo:
Si calcola la rappresentazione vettoriale di \(y\) utilizzando la pesatura tf-idf.
Si calcola la cosine similarity per ogni coppia di vettori \(\underline{y}\) e \(\underline{x}\), al variare di \(x\) nel training set \(D\), e si ordinano i vettori rispetto a questi valori.
Si prendono i \(k\) vettori del training set più vicini al vettore \(\underline{y}\) e si ritorna la categoria di maggioranza tra i \(k\) vettori considerati.
Notiamo che i vector space models che abbiamo descritto hanno un numero elevato di dimensioni, in quanto tipicamente i dizionari hanno un numero elevato di parole. I documenti però contengono solamente una piccola frazione delle parole presenti in un dizionario. Questo significa che utilizzando un vector space model i documenti vengono rappresentati con dei vettori molto sparsi, che sono principalmente formati da coordinate con valore \(0\), e che hanno poche coordinate con valori \(\ge 0\).
Il task di ridurre le dimensioni di uno spazio vettoriale mantenendo comunque delle relazioni significative tra i vettori dello spazio prende il nome di dimensionality reduction.
Per affrontare questo task, un primo approccio sarebbe quello di eliminare le parole poco significative dal dizionario. Questa tecnica prende il nome di feature reduction, in quanto stiamo diminuendo le features (parole) che utilizziamo per costruire il nostro spazio vettoriale. In generale siamo quindi interessati a dei metodi che ci permettono di trovare un nuovo spazio vettoriale di dimensione \(M\) con molto più piccolo della dimensione originale \(M \ll N\).
Il clustering è una tecnica che può essere utilizzata per diminuire le dimensioni di uno spazio vettoriale, andando a diminuire la complessità dei task successivi che vogliamo risolvere. Tramite il clustering quindi possiamo raggruppare vettori associati a più documenti tra loro, in modo da averne una descrizione più compatta.
Il clustering si basa sui tre seguenti elementi:
Rappresentazione vettoriale degli oggetti di interesse (che possono essere documenti) tramite una pesatura delle features degli oggetti (che può essere la tf-idf).
Definizione di una misura di prossimità.
Utilizzo di un algoritmo di clustering.
Valutazione del cluster ottenuto.
Il k-mean è un noto algoritmo di clustering ed è descritto come segue:
Consideriamo un insieme \(E\) di punti nello spazio.

Per iniziare l'algoritmo sceglie due punti \(x\) e \(y\) in modo completameante arbitrario. Una volta scelti i punti si assegnano i punti restanti ai due clusters in base alla distanza: in particolare ad ogni punto \(z\) si assegna il cluster il cui centroide è più vicino.
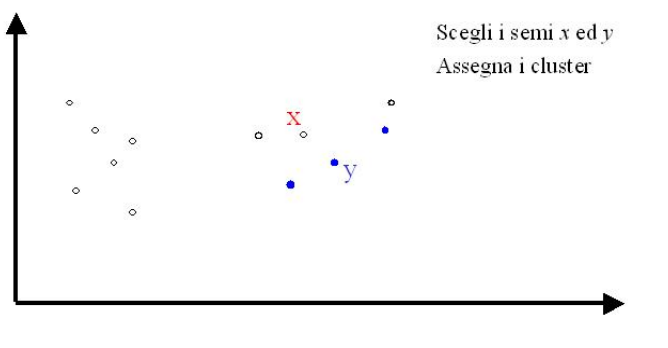
Una volta che abbiamo assegnato un cluster ad ogni punto procediamo andando a calcolare, per ogni cluster, i nuovi centroidi. Questo calcolo viene effettuato andando a calcolare, all'interno di ogni cluster, il punto medio degli elementi del cluster.

Dopo aver spostato i centroidi di ogni cluster, procediamo ripetendo l'assegnazione dei punti ai cluster, che viene fatta come prima sempre in base alla distanza.
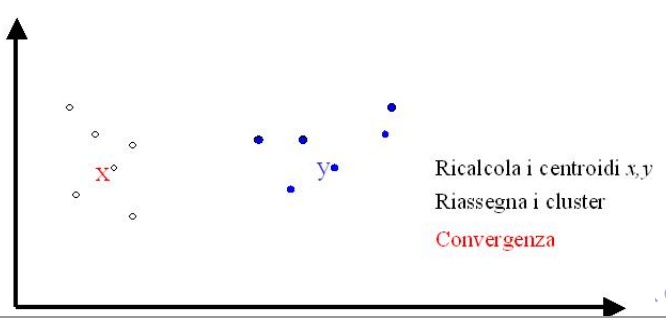
Il processo termina quando c'è una convergenza rispetto alla posizione dei centroidi e al numero di punti che cambiano cluster ad ogni iterazione.
Nel processo di clustering risulta fondamentale non solo avere uno spazio vettoriale, ma anche una misura di prossimità che mappa ogni coppia di elementi del nostro spazio ad un numero reale. La scelta di questa misura ha un impatto decisivo sulla qualità dei vari clusters costruiti.
Per i problemi geometrici la distanza standard utilizzata è la distanza di Minkowski, denotata con \(L_p(\underline{x}, \underline{y})\) e definita come segue
\[L_p(\underline{x}, \underline{y}) = \sqrt[p]{\sum_{i = 1}^n | x_i - y_i |^p}\]
La distanza di minkowski è la generalizzazione della distanza euclidea, in quanto per \(p = 2\) otteniamo esattamente la distanza euclidea in uno spazio n-dimensionale. Se invece \(p \to \infty\) allora sarà la distanza maggiore tra le varie coordinate che domina e otteniamo
\[L_p(\underline{x}, \underline{y}) = \text{argmax} \,\, | x_i - y_i |\]
Se poi \(p = 1\) allora otteniamo la Manhattan distance, che conta il numero di differenze tra gli oggetti.
Una volta che abbiamo una distanza metrica come la distanza di Minkowski \(L_p(\underline{x}, \underline{y})\) definita prima, possiamo convertire questa distanza, che varia in \([0, \infty)\), in una misura di similarità che varia in \([0, 1]\) tramite l'utilizzo di una funzione monotona decrescente. Ad esempio, per gli spazi euclidei possiamo correlare la distanza \(d\) tra due vettori con la loro similarità \(s\) nel seguente modo
\[s = e^{-d^2}\]
Dalla formula si evince che, al crescere di \(d\), ovvero al crescere della distanza, la similarità decresce in modo esponenziale. Conseguentemente, la similarità normalizzata euclidea è data da
\[s^{(E)}(x, y) = e^{-||x - y||^2_2}\]
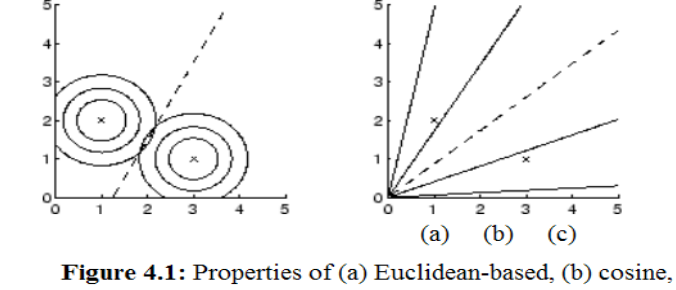
La similarità tipicamente può variare rispetto a due dimensioni, che sono la scala e la traslazione. Una metrica di similarità infatti può essere:
Invariante alla scala: quando non dipende dalle variazioni sulla scala e quindi non risente della dimensione dei vettori.
Invariante alla traslazione: quando non risente della posizione del vettore nel piano.
La metrica di similarità euclidea è detta translation invariant, in quanto è inviarante alla traslazione, ma è fortemente dipendente dalla scala. La cosine distance invece è una metrica di similarità detta scale invariant, in quanto non dipende dalla scala dei vettori, ma è translation sensitive.
I seguenti grafici fanno vedere le caratteristiche delle varie metriche descritte.