WMR 04 - Geometrical Models II
Date:
Course Site: Web Mining e Retrieval (a.a. 2019/20)
Lecturer: Roberto Basili
Slides: (wmr_03.pdf)
Table of Contents:
In questa lezione abbiamo commentato assieme qualche aspetto della lezione precedente riguardante la dimensionality reduction e abbiamo poi continuato a parlare di funzioni di similarità probabilistiche.
Che cosa c'entra il clustering con il modello geometrico?
Consideriamo il problema della text classification. Come abbiamo già notato, un approccio tipico per risolvere la text classification è quello di utilizzare un vector space model e associare ad ogni documento un vettore. Per fare questo si può, ad esempio, utilizzare la pesatura tf-idf che associa ad un termine (dimensione nello spazio vettoriale, e quindi coordinata della rappresentazione vettoriale del documento) un determinato peso.
In questo approccio però i vettori tipicamente sono vettori molto sparsi, ovvero hanno molte coordinate a 0, in quanto in un singolo documento, tipicamente, c'è solo una frazione limitata del vocabolario dell'intera collezione documentale.
Per cercare di ridurre la dimensione dei vettori si possono utilizzare varie tecniche di dimensionality reduction. Tipicamente queste tecniche possono essere raggruppate in tre famiglie diverse:
Tecniche statistiche
Tecniche di ricostruzione
Tecniche di algebra lineare
Un esempio di tecnica statistica è la feature selection, che consiste, nel contesto della text classification, di buttare via le parole troppo rare e poco utili prima di costruire lo spazio vettoriale. L'idea è che se una parola è troppo rara, nel training set tendiamo inevitabilmente a sopravvalutare il suo ruolo.
Esempio: se nel nostro taining set troviamo la parola "cornuto" in un articolo che parla di sport, non signifa che la parola "cornuto" è significativa per il contesto dello sport.
Esistono poi dei metodi che si basano su verità matematiche, ad esempio le tecniche di ricostruzione, che tramite una matrice di costruzione posso ricostruire un punto nello spazio \(\mathbb{R}^3\) utilizzando solamente due punti in \(\mathbb{R}^2\) e mantenendomi le distanze del punto tra i due punti di \(\mathbb{R}^2\).
Il clustering in questo contesto ci può dare una strategia per scegliere i rappresentati che possiamo utilizzare per effettuare la dimensionality reduction tramite questa ricostruzione: per ogni cluster infatti possiamo eleggere un rappresentate, e le distanze del punto di interesse ai vari rappresentati vengono quindi utilizzate per piazzare il punto nello spazio. Così facendo posso utilizzare un numero ristretto di coordinate per classificare le distanze.
Il clustering poi può anche essere utilizzato per fare la classificazione in un contesto supervisionato nel seguente modo: considero il cluster più vicino al mio punto e assegno al punto la classe di maggiranza presente nel cluster. Questo tipo di classificazione è simile al kNN, ma procede con un \(k\) variabile, in quanto ogni cluster ha un numero di elementi variabili.
Queste tecniche di ricostruzione con clustering vengono molto spesso utilizzare per combinare pochi dati annotati con una sconfinata serie di dati non etichettati che mi permettono di semplificare lo spazio in cui lavoro.
Come terzo modello di dimensionality reduction possiamo agire non facendo clustering ma agendo sulla distribuzione dei dati con tecniche di algebra lineare.
Nel semi-supervised learning, ad esempio, i dati reali ci discono la topologia in cui si distribuisce lo spazio metrico, mentre i dati etichettati mi consente di applicare un algoritmo supervised. Questi schemi si basano sui seguenti steps:
Cambio lo spazio (semplificandolo), grazie ai dati reali non etichettati.
Addestro una funzione più facile da derivare con meno esempi.
Nella scorsa lezione abbiamo visto la distanze come concetto geometrico introducendo la distanza euclidea e quella di minkowski. I concetti di distanza e similarità però possono sviluppati anche a partire da altre basi.
Ad esempio possiamo considerare delle funzioni di similarità che si basano su proprietà probabilistiche/statistiche. Ad ogni proprietà (es: l'età di una persona) posso associare una distribuzione di probabilità. La distanza tra due vettori deve quindi tener conto delle probabilità, e non solo dei numeri. In questo contesto diciamo quindi che due vettori sono simili se le probabilità delle caratteristche di interesse dei vettori sono simili.
I fuzzy sets sono una generalizzazione degli insiemi standard. Ad ogni insieme standard \(A\) è infatti possibile associare una funzione caratteristica \(\chi_A\) che associa ad ogni elemento del nostro universo un valore \([0,1]\) in modo deterministico. Generalizzando questo concetto, possiamo avere una funzione caratteristica non più deterministica ma che associa ad ogni elemento un valore preso dall'intervallo \([0, 1]\) che quindi può essere considerato un valore di probabilità.
A partire dai fuzzy sets è possibile definire delle funzioni che misurano la distanza tra due insiemi.
Osservazione: I fuzzy set possono essere utilizzati in modo completamente empirico. Ad esempio possono essere utilizzati per esprimere il concetto di "essere giovani". L'origine dei fuzzy set può essere definita formalmente o in base ai dati. Tipicamente vengono definiti utilizzando dei trapezoidi.
Consideriamo adesso la correlazione con un caso specifico.
Supponiamo di avere due oggetti (film), \(x\) e \(y\), e una pool di critici \(m_1, \ldots, m_n\) che giudicano ciascun film con uno score. In particolare il giudice \(m_i\) giudica il film \(x\) con lo score \(x_i\) e il film \(y\) con lo score \(y_i\). Diremo che due film sono simili tra loro se i due film ricevono score simili dagli stessi giudici.
Dati i vettori \(\overline{x}\) e \(\mathbf{y}\) che contengono tutti i vari giudizi \(x_i\) e \(y_i\), possiamo calcolare delle features riassuntive quali la media e la standard deviation. Il nostro obiettivo è quindi calcolare l'analogia tra gli oggetti \(x\) e \(y\) calcolando la correlazione tra i vettori \(\overline{x}\) e \(\overline{y}\).
La similarità di Pearson \(s^{(P)}\) (o Pearson correlation) è calcolata in funzione sia dei giudizi individuali e sia dei giudizi medi ed è così definita
\[s^{(P)}(\overline{x}, \overline{y}) := \frac{1}{2}\Bigg(\frac{(\overline{x} - \mu_{\overline{x}})^T \cdot (\overline{y} - \mu_{\overline{y}})}{||\overline{x} - \mu_{\overline{x}}||_2 \cdot || \overline{y} - \mu_{\overline{y}}||_2} + 1 \Bigg)\]
dove la quantità viene normalizzata in modo da ottenere un valore compreso tra \([0, 1]\).
Notiamo che così facendo se \(x\) è giudicato in modo medio simile ad \(y\), allora la loro similarità tramite il coefficiente di pearson è alta. In generale a noi questo interessa in quanto vogliamo tipicamente nel machine learning vogliamo capire come un oggetto si comporta rispetto ad \(n\) fonti, tutte indipendenti tra loro. Il valore del coefficiente di Pearson può essere utilizzato per raccomandare oggetti utilizzando la similarità dei giudizi.
Il coefficiente di Jaccard è una misura che conta il numero di elementi condivisi tra due insiemi. Il coefficiente di Jaccard tra due insiemi \(A\) e \(B\) può essere ottenuto calcolando il prodotto scalare tra i due vettori indicatori dei set \(A\) e \(B\). In formula,
\[J(A, B) = \frac{A \cap B}{A \cup B}\]
Il coefficiente di Jaccard viene molto spesso utilizzato nelle reatail market-basket applications. È poi possibile estendere il coefficiente di Jaccard ad un qualsiasi vettore con coordinate in [0, 1] nel seguente modo
\[s^{(J)}(\overline{x}, \overline{y}) = \frac{\overline{x}^T \overline{y}}{||\overline{x}||_2^2 + ||\overline{y}||_2^y - \overline{x}^T \overline{y}}\]
Il coefficiente di Jaccard esteso è sia scale sensitive che translation sensitive.
Un coefficiente simile a quello di Jaccard è il coefficiente di Dice, definito come segue
\[s^{(D)}(\overline{x}, \overline{y}) = \frac{2 \overline{x}^T \overline{y}}{||\overline{x}||_2^2 + ||\overline{y}||_2^2}\]
Nel clustering tradizionale visto nella precedente lezione si utilizza la distanza Euclidea per calcolare il rappresentate ottimale per ciascun cluster, ovvero ovvero il punto che minimizza lo squared error.
\[c_l = \underset{\overline{z} \in \mathcal{F}}{\text{arg min}} \sum\limits_{\overline{x}_j \in \mathcal{C}_l} || \overline{x}_j - \overline{z} ||_2^2\]
Al posto di utilizzare la distanza come funziona obiettivo, possiamo però utilizzare la trasformazione
\[s = e^{-d^2}\]
per esprimere la funzione obiettivo in termine della similarità piuttosto che in termine della distanza. In questo modo pensiamo al clustering non come la minimizzazione delle distanze, ma come la massimizzazione della similarità.
\[\sum\limits_{\overline{x}_j \in \mathcal{C}_l} -\log{(s(\overline{s}_j, \overline{z}))}\]
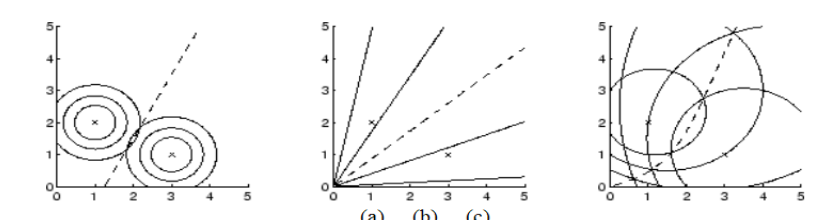
Più che concentrarci sull'algoritmo, l'idea è quella di concentrarci sulla rappresentazione. L'utilizzo di spazi metrici con funzioni di distanza diversi produce infatti dei modelli diversi tra loro.
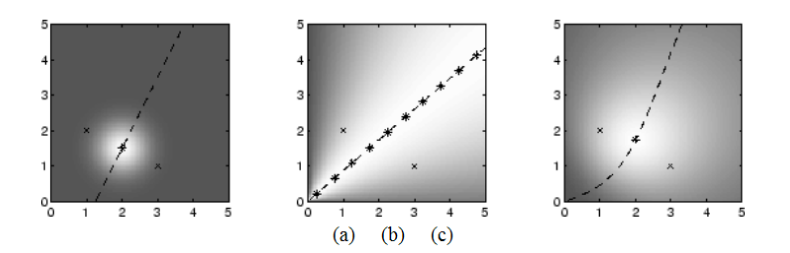
Abbiamo quindi leggi che possono essere lineari sotto una certa metrica, e avere comportamenti non lineari sotto metriche diverse. È Proprio per questa ragione che nel machine learning è di fondamentale importanza capire qual è lo spazio giusto e la metrica giusta con cui lavorare.
La scelta della rappresentazione, delle metriche, e degli algoritmi di induzioni sono molto correlati tra loro. Non esiste un algoritmo che funziona per tutte le rappresentazioni, come non esiste una rappresentazione che funziona con tutti gli algoritmi. Sono i dati da processare e il task da risolvere che ci devono suggerire lo spazio di rappresentazione e la metrica utilizzata.
Osservazione: Interpretando la similarità come probabilità, otteniamo poi un modello probabilistico. I classificatori bayesiani infatti sono classificatori lineari nello spazio delle similarità.
Q1: Perché passiamo da distanza a similarità?
A1: Perché i concetti di distanza e similarità sono uno il duale dell'altro. Ho quindi due metodi diversi per guardare lo stesso problema. La particolare funzione \(e^{-f(d)}\) è solo un modo in cui possiamo passare dalla distanza alla similarità. L'importante comunque è che la funzione sia monotonica e descrescente, in quanto più la distanza aumenta e più la similarità deve diminuire.