WMR 05 - Naive Bayes Classifier I
Date:
Course Site: Web Mining e Retrieval (a.a. 2019/20)
Lecturer: Roberto Basili
Slides: (wmr_04.pdf)
Table of Contents:
In questa lezione abbiamo introdotto il primo modello di Naive Bayes Classifiers per risolvere il problema della text classification: I multivariate binomial classifiers, che modellano un documento come \(n\) varibili aleatorie binarie ed indipendenti. Abbiamo poi terminato la lezione discutendo delle criticità di tale modello.
Data la difficoltà nel definire in modo formale e preciso delle regole che ci permettano di stabilire la "natura" di un documento, affrontare il problema della classificazione dei testi utilizzando tecniche di apprendimento automatico può essere molto utile, specialmente nel contesto del web, in cui la maggior parte dei contenuti sono contenuti in forma testuale all'interno di documenti.
Un chiaro esempio di text classification ci è dato nel contesto delle e-mail, in cui il concetto di spam è un qualcosa di molto aleatorio, che dipende, tra le altre cose, anche dalla persona che sta leggendo la e-mail. Saper classificare quali e-mail sono spam e quali non lo sono è dunque un problema molto importante da saper risolvere bene.
La domanda che ci dobbiamo porre quindi è la seguente: come possiamo indurre la funzione di categorizzazione dai dati a partire dai dati di training?
Il problema che vogliamo risolvere è così descritto: data una descrizione di una istanza \(x \in X\), dove \(X\) rappresenta lo spazio delle istanze, e dato un insieme fisso di categorie \(C = \{C_1, C_2, ..., C_n\}\), si vuole determinare quali sono le categorie associabili all'istanza \(x\), ovvero il sottoinsieme \(c(x) \subseteq C\).
Dalla definizione del problema risultano chiare immedatamente due problematiche da affrontare. Queste sono:
Come rappresentiamo i documenti?
Come possiamo costruire la funzione di classificazione \(c(\cdot)\)?
Quando guardiamo i dati di training, rappresentati dai documenti, possiamo acquisire da essi un insieme di parole che rappresentano i documenti. Molto spesso poi il modello utilizzato per rappresentare i documenti prende il nome di modello bag of words, in quanto ciascuna parola costituisce un segnale indipendente dagli altri, e si tiene traccia solo delle ripetizioni delle parole, e non delle relative posizioni. In altre parole, vediamo un documento come un insieme di parole in cui a ciascuna parola è associata una frequenza.
La classificazione testuale può essere applicata a vari contesti, tra cui:
Topics tra articoli di giornali: finance, sports, news.
Generi tra articoli d giornali: editorials, movie-reviews, news.
Opinioni tra commenti: like, hate, neutral.
Domain-specific binary, come:
"interesting-to-me", "not-interesting-to-me"
"spam", "not-spam"
"is fake", "is not fake"
Possiamo affrontare il problema della text classification in vari modi. Tra questi troviamo anche i seguenti
Molto accurata quando viene fatta da esperti, e tende a non contraddirsi nel tempo rispetto alla taglia del problema affrontato e i gruppi di persone che lavorano alla classificazione.
Tipicamente questo lavoro viene fatto utilizzando delle basic rules come le seguenti, che agiscono in funzione del contenuto del documento e che possono essere combinate tra loro. Principalmente le regole lavorano su:
Lexical items: Come le parole, i nomi, e via dicendo.
Metadati: Come l'autore, la data di pubblicazione, la data di scrittura, e via dicendo.
Sorgenti: Il luogo in cui è stata pubblicata e da cui è stata condivisa.
Anche se ha molti lati positivi, la classificazione manuale del testo è anche molto costosa ed è difficile da far scalare rispetto al numero di documenti da classificare. Per queste ragioni con il passare del tempo e il crescere dei documenti presenti nel web si sono adottate sempre di più soluzioni automatiche.
Per cercare di risolvere il problema delle performance su grandi mole di dati, si è quindi pensati di cercare di automatizzare la risoluzione di tale problema. I possibili approcci automatici sono principalmente due:
Hand-coded rule-based systems: questi sistemi sono basati su regole discrete che utilizzano dei pattern grammaticali, come forme frasali o nomi, per classificare il testo. Anche se possono essere efficienti, questi sistemi hanno dei problemi di manutenzione e tendono ad essere troppo costosi.
Supervised learning (data-driven): l'idea qui è quella di utilizzare degli algoritmi di apprendimento assieme a dei dati già annotati (training set) per produrre dei modelli di classificazione. Tra questi metodi troviamo:
k-NN (simple, powerful)
Rocchio (geometry based, simple, effective)
Naive Bayes (simple, common)
...
Support-vector machines, neural networks (very accurate)
Concetto di no free lunch: i dati iniziali devono essere annotati, e trovare il giusto dataset può essere molto difficile. Negli ultimi anni si stanno adottando sempre di più metodi di crowdsourcing, che consistono nel coinvolgere utenti nella rete per annotare piccole porzioni di datasets. Questa annotazione fatta da utenti inesperti può essere sia utilizzata nelle fase di bootstrapping dei sistemi sia per cercare di migliorare il comportamento modello su dei dati critici.
Molto spesso questi due approcci vengono combinati tra loro.
I metodi bayesiani sono basati sulla sulla probabilità. In particolare il modello indotto dai dati ci deve dare una spiegazione probabilistica delle categorie che si avvicini il più possibile alla "ideale" funzione di classificazione.
L'idea sottostante a questi metodi è quella di costruire dei modelli generativi per ogni tipologia di documenti (sport, finanza), che ci permettono di capire la struttura delle varie tipologie di documenti. In tali modelli abbiamo due tipologie di proprietà:
Proprietà osservabili: Possono essere facilmente osservabili, come la parole di un testo.
Proprietà nascoste: Non possono essere osservate anche se sono alla base di quelle osservabili.
Il modello generativo è quindi il modello che descrive il modo in cui le variabili nascoste generano le parole che osserviamo. Per descrivere queste proprietà non osservabili utilizziamo la probabilità. In particolare la prior probability è la probabilità da cui possiamo iniziale e non è basata sul contenuto che stiamo analizzando. Partendo dalla prior probability e utilizzando il modello generativo posso poi ottenere la posterior probability.
Per ribaltare la relazione tra cause ed effetto nella generazione dei documenti utilizziamo la famosa Baye's Rule.
Consideriamo una istanza \(X\) che rappresenta un doc. e una categoria \(C\). Consideriamo adesso la probabilità che l'istanza \(X\) parla dell'argomento \(C\), espressa con \(P(C, X)\). Dal calcolo della probabilità abbiamo che
\[P(C, X) = P(C | X) \cdot P(X) = P(X | C) \cdot P(C)\]
Dove,
\(P(X | C)\) è probabilità che gli articoli che parlano della categoria \(C\) utilizzano la parola \(X\).
\(P(C | X)\) è probabilità che la parola \(X\) è utilizzata nei documenti della categoria \(C\).
Da questa simmetria dell'evento congiunto e dal fatto che \(P(C, X) = P(X|C) \cdot P(C)\), possiamo quindi ottenere la menzionata regola di Bayes
\[P(C | X) = \frac{P(X|C) \cdot P(C)}{P(X)}\]
Sia \(H\) l'insieme delle categorie, e sia \(X\) un documento. L'approccio MAP (Maximum a Posteriori Hypothesis) assegna ad \(X\) la categoria \(h_{\text{MAP}}\) tale che
\[\begin{split} h_{\text{MAP}} &= \underset{h \in H}{\text{argmax}} P(h|X) \\ &= \underset{h \in H}{\text{argmax}} \frac{P(X|h) P(h)}{P(X)} \\ &= \underset{h \in H}{\text{argmax}} P(X|h) P(h) \\ \end{split}\]
Come possiamo vedere quindi \(h_{\text{MAP}}\) rappresenta la categoria che massimizza la probabilità a posteriori \(P(h|X)\). Per calcolarmi tale massimo poi devo solo avere a disposizione la probabilità a priori \(P(h)\), che posso assumere di avere per ogni categoria \(h \in H\), e la likelihood di vedere \(X\) nella categoria di \(h\), che posso calcolare a partire dai dati di training.
Il task che vogliamo risolvere consiste nel classificare una istanza di un documento \(D\) basandosi su una tupla di valori di attributi \(D=(x_1, ..., x_n)\) in una delle classi \(C_j \in C\).
Per risolvere questo task si utilizza la maxium a posteriori hypothesis, ovvero si sceglie la classe che massimizza la probabilità \(P(C_j | x_1, x_2, ..., x_n)\). Supponendo infatti di conoscere la probabilità a priori per ogni classe \(P(C_j)\), e la probabilità di generazione dei valori delle proprietà \(P(x_1, x_2, ..., x_n | C_j)\), possiamo calcolare la classe che massimizza la probabilità a posteriori \(P(C_j | x_1, x_2, ..., x_n)\).
In termine di machine learning, modellare in forma bayesian un problema consiste nel risolvere i seguenti quattro aspetti progettuali:
Formalizzare l'insieme delle proprietà osservabili dato un documento e rappresentare il concetto di documento come l'evento congiunto delle seguenti proprietà
\[D = \big(x_1, x_2, ..., x_n\big) = \big(x_1^D, x_2^D, \ldots, x_n^D\big)\]
Determinare il modo in cui il contenuto del documento determina il valore della proprietà \(x_i\).
Determinare come stimare le seguenti probabilità:
\(P(C_j)\) per ogni classe.
\(P(X^D_i)\) per le diverse features.
\(P(X^D_1, x^D_2, \ldots, X^D_n | C_j)\) per diverse tuple e diverse classi.
Definire la legge che ci permette di scegliere quale categoria assegnare a quale documento:
argmax.
best m scores.
thresholds.
Notiamo che i punti (1) e (2) sono problemi di rappresentazione, il punto (3) è l'estimation problem mentre il punto (4) è il problema dell'inferenza.
Concentriamoci adesso sui punti (1) e (2). L'idea è quella di utilizzare le parole e le loro occorrenze nel documento come dei "segnali" rispetto al contenuto del documento. Possiamo quindi pensare alle parole come ai risultati di un test sperimentale, e possiamo modellare questo test sperimentale come una variabile aleatoria \(X\). Avere come risultato \(x_i\) sta quindi a significare che il risultato dell'esperimento aleatorio ha dato come risultato l'i-esima parola. Dato un test, più occorrenze ci sono per quella parola e più alta sarà la probabilità di tirare fuori esattamente quella parola.
\[p(x_i) = P(X = \text{word}_i)\]
Un modo per modellare il documento consiste quindi nel rappresentare il documento \(D\) come un enorme esperimento in cui provo a pescare ogni possibile parola del vocabolario. Per ogni parola potrò quindi avere present se questa è presente nel documento \(D\), oppure not present, se questa non è presente nel documento \(D\). Così facendo stiamo dicendo che ogni proprietà osservabile (feature) del nostro modello Bayesiano sta modellando la presenza o l'assenza di una determinata parola.
Per formalizzare il tutto possiamo quindi associare ad ogni parola del vocabolario una variabile aleatoria \(x_i\) tale che
\[x_i = \begin{cases} 0 \;\;,& \; \text{la parola } i \text{ esima è assente dal documento} \\ 1 \;\;,& \; \text{la parola } i \text{ esima è presente dal documento} \\ \end{cases}\]
Così facendo abbiamo che utilizziamo \(n=|V|\) variabili aleatorie per rappresentare ogni documento, dove \(|V|\) è il size del vocabolario. Questo modello è chiamato multivariate binominal model, in quanto:
multivariate, perché vengono utilizzate più variabili.
binomial, perché ciascuna variabile può assumere solo due valori.
Siamo quindi arrivati al punto in cui dobbiamo stimare le varie probabilità. A tale fine possiamo procedere come segue:
Per quanto riguarda la prior probability delle varie classi \(P(C_j)\), tale probabilità può essere stimata dalla frequenza della classe \(C_j\) nel training set. In particolare quindi si fa
\[\hat{P}(C_j) = \frac{\text{# docs in classe } C_j}{\text{# docs totale}}\]
Per quanto riguarda invece la likelihood \(P(x_1, x_2, ..., x_n | C_j)\), tale probabilità è più difficile da stimare, in quanto abbiamo \(O(|x|^n \cdot |C|)\) parametri da stimare, e quindi siamo in grado di stimarla solamente utilizzando un sacco di esempi di training. In generale infatti più eventi devo stimare e più grande il dataset di training deve essere. Se poi i parametri sono troppo numerosi, come in questo caso, pensare di stimarli tutti diventa impossibile.
Per semplificare questo problema si introduce la naive bayes conditional independence assumption, che dice che fissata una categoria le parole generate nella stessa categoria sono indipendenti l'una dall'altra. In formula che gli eventi \(P(x_i | C_j)\) sono indipendenti al variare di \(i\). Così facendo ottengo la seguente espressione
\[P(x_1, x_2, ..., x_n | C_j) = \prod\limits_{i = 1}^n P(x_i | C_j)\]
Osserviamo che adesso il numero di parametri è diventato \(O(|X| \cdot |C|)\), il che ci permette di stimare i vari parametri in modo abbastanza tranquillo tramite la seguente formula
\[\hat{P}(x_i | C_j) = \frac{\text{# occorrenze di } x_i \text{ nella classe } C_j}{\text{# occorrenze nella classe } C_j}\]
Il seguente algoritmo mette assieme quanto discusso prima per effettuare il passo di learning del modello

I valori \(+1\) e \(+2\) presenti nel calcolo della probabilità condizionata sono legati ai concetti di normalizzazione e smoothing che vengono utilizzati per aumentare la robustezza delle stime ottenute. In particolare se un termine \(t\) non compare mai nei documenti di classe \(C\), non è detto che anche nel futuro il termine \(t\) non apparirà mai in documenti di classe \(C\). In altre parole, gli eventi rari non sono impossibili. Per non far azzerare le probabilità aggiungo quel \(+1\) al nominatore. Lo smoothing permette quindi di redistribuire una parte di probabilità del campione sugli eventi rari, in modo tale che il modello è in grado di gestire anche gli eventi rari. Andando a rimuovere quel \(+1\) potremmo finire in situazioni di overfitting.
Possiamo rappresentare graficamente la situazione appena modellata nel seguente modo
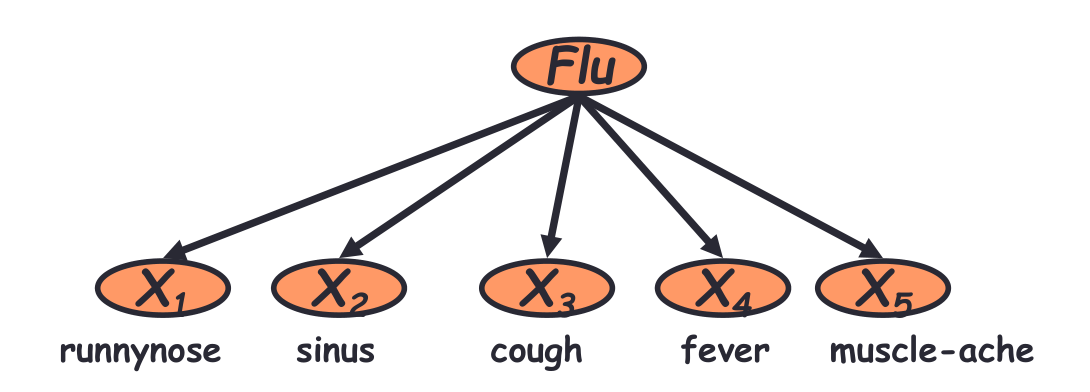
Come possiamo vedere, gli eventi osservabili sono i vari sintomi, come fever, muscle-ache, e via dicendo. Tutti questi però sono generati dall'influenza, che non possiamo osservare direttamente.
L'ipotesi di indipendenza naive bayes in questo contesto ci sta dicendo che ciascun sintomo è indipendente dagli altri.
Una volta che abbiamo addesstrato il modello e abbiamo ottenuto le prior e le conditional probabilities, possiamo applicare il modello ad un qualsiasi documento \(d\).
I parametri ottenuti dall'addestramento sono:
V, vocabolario.
prior, prior probabilities.
cond prob, conditional probabilities.
Il modo in cui scegliamo la legge da applicare per effettuare le inferenze sulla appartenenza di un documento ad una classe dipende molto dal particolare task che vogliamo risolvere. Inparticolare,
L'argmax è applicabile per tutti i task in cui ogni documento ammette una e una sola classe. In questi casi l'argmax è la scelta migliore che posso effettuare.
Se ogni oggetto ha un numero fissato di categorie (n>1), e vogliamo almeno \(n\) categorie per ogni oggetto, possiamo ordinare le varie probabiità dalla più grande alla più piccola, prendendo le prime \(n\) categorie.
Se non conosco il numero delle categorie per tutti i documenti, ovvero se il numero di categorie che devo assegnare ai documenti varia da documento a documento, posso definire dei valori di threshold e accettare che il documento parla di un argomento quando supera il valore di threshold per quella particolare categoria. Le thresholds vengono molto spesso stipulate a seconda della categoria.
Considerando una classificazione ad una sola classe, possiamo applicare l'argmax e ottenere il seguente algoritmo di inferenza

Per ottenere il vocabolario delle parole si procede con la seguente processing chain:
Elimino dal testo le stop words, ovvero le occorrenze delle parole "non significative" da un punto di vista informatico
Normalizzo le parole restanti andandole a rappresentare in una forma comune: ad esempio singolari e plurali vengono normalizzati ad una forma comune, chiamata lemma.
Dopo aver effettuato questi (e potenzialmente tanti altri steps) posso utilizzare il vocabolario per effettuare il learning del modello descritto prima.
A seguire riportiamo due criticità nell'applicazione di un classificatore Naive Bayes:
Independence Assumption: L'assunzione di indipendenza naive ci porta al fatto che eventi rari, che possono non essere presenti nel nostro dataset di training, sono considerati impossibili. Per stimare la probabilità condizionata infatti moltiplichiamo le varie probabilità tra loro, ed eventi non presenti nel dataset hanno probabilità a \(0\).
Per cercare di risolvere questo problema un possibile approccio potrebbe essere quello di associare una probabilità \(> 0\) anche agli eventi rari non presenti nel dataset. In formula,
\[\hat{P}(x_i | C_j) = \frac{N(X = x_i | C = C_j) + 1}{N(C = C_j) + 1 \cdot p}\]
dove \(p\) è il numero di volte in cui ho aggiunto questo fattore di smoothing. Nel caso binomiale visto in precedenza abbiamo che \(p = 2\).
Un'altra tecnica di smoothing più sottile prende il nome di Laplace Smoothing, e consiste nel considerare che ogni feature ha una prior probability di \(p\) e di assumere che ogni parola è stata vista \(m\) volte in una serie di esempi virtuali prima ancora di guardare al training set. Con questo approccio la formula dello smoothing diventa,
\[P(x_i | C_j) = \frac {N(X = x_i | C = C_j) + m \cdot p} {(N(C = C_j) + m}\]
Tipicamente si assume una probabilità uniforme su tutti i termini, ovvero si pone \(p = 1/|V|\), \(m=|V|\). Questi parametri modellano la situazione in cui tutte le parole del dizionario vengono viste almeno una volta, anche se non compaiono nel training set.
Osservazione: Ci sono poi delle formulazioni ancora più complesse, che cercano di raggruppare eventi speciali simili tra loro in gruppi, chiamati bins, a cui poi viene associata una probabilità \(p_{i.k}\). Un tipico caso è quello in cui i bins sono scelti in base alla frequenza delle parole.
Underflow Prevention: Per cercare di evitare relativi problemi di floating-point underflow l'idea è quella di effettuare le operazioni utilizzando il logaritmo, in quanto il logaritmo ci permette di trasformare prodotti in somme.
Notiamo che dalle proprietà della funzione logaritmo, ovvero il fatto che è una funzione monotona crescente, abbiamo che l'argmax dell'espression originale è uguale all'argmax dell'espressione con il logaritmo.
Così facendo riconduciamo l'argmax di un prodotto all'argmax di una somma.