WMR 06 - Naive Bayes Classifier II
Date:
Course Site: Web Mining e Retrieval (a.a. 2019/20)
Lecturer: Roberto Basili
Slides: (wmr_05.pdf)
Table of Contents:
Nel modello multivariato binomiale introdotto la scorsa lezione avevamo rappresentato il documento \(D\) come l'evento congiunto dell'estrazione di tutte le parole dal dizionario in modo da verificare quale di queste erano presenti nel documento \(D\). Questo impone l'utilizzo di \(n = |V|\) features, e dato che i vocabolari sono tendenzialmente molto grandi, la conseguenza di questo approccio è che dobbiamo utilizzare molte features per rappresentare un documento \(D\).
Poniamoci ora il seguente quesito: è possibile rappresentare il documento in un modo migliore, un modo che ad esempio utilizzerebbe meno features? La risposta a questa domanda, fortunatamente, è positiva, e sarà l'oggetto della lezione.
Consideriamo il documento \(D\) come un insieme di \(m\) posizioni distinte, dove \(m\) è il size del documento \(D\). Un modo alternativo di rappresentare il documento è come la congiunzione degli eventi \(X_1, X_2, ..., X_m\), dove l'evento \(X_i\) rappresenta l'esperimento di estrarre un termine dal vocabolario e inserirlo nella \(i\) - esima posizione del documento \(D\).
In questo modo siamo passati da un modello multivariate binomial ad un modello multivariate multinomial, in quanto:
Multivariate: Ho sempre più variabili aleatorie per descrivere un singolo documento.
Multinomial: A differenza del modello di prima, in cui ogni variabile poteva assumere un valore binario (1 per presente e 0 per assente), adesso ciascuna feature è una parola, e può quindi assumere \(|V|\) valori diversi tra loro.
Parlare di posizioni significa parlare di sequenze. Le sequenze a cui stiamo facendo riferimento poi sono sequenze di parole, che vengono anche chiamate stringhe. Le stringhe che vediamo nei documenti rappresentano quindi possibili espressioni nella lingua in analisi. Per studiare queste sequenze di stringhe possiamo utilizzare la teoria dei modelli di linguaggio.
I modelli di linguaggio vengono utilizzati per stimare le probabilità di generare una particolare stringa del linguaggio analizzato. A seconda della complessità del modello possiamo avere varie ipotesi di indipendenza tra le parole.
In questo modello si assume che l'occorrenza di ciascuna parola nella stringa generata è indipendente dalle altre parole.
Con questa assunzione, chiaramente astratta e semplificativa, per calcolare la probabilità di generare una data stringa devo semplicemente moltiplicare la probabilità di generare ogni parola all'interno della stringa. In formula,
\[P(a_1, a_2, \ldots, a_n) = P(a_1) \cdot P(a_2) \cdot \ldots \cdot P(a_n)\]
Notiamo che questo modello è troppo semplice, e non riesce a catturare la dipendenza dal contesto delle parole.
In questo modello invece si assume che l'occorrenza di una parola in posizione \(i\) dipenda solamente dalla parola precedente in posizione \(i-1\). In formula,
\[P(a_1, a_2, \ldots, a_n) = P(a_1) \cdot P(a_2 | a_1) \cdot (a_3 | a_2) \cdot \ldots \cdot P(a_n | a_{n-1})\]
Generalizzazione di quanto visto prima, nel modello \(n\) gram ogni parola dipende solamente dalle \(n-1\) parole generate precedentemente.
Con questo modello al crescere di \(n\) riesco sempre di più a catturare la dipendenza dal contesto delle parole. Detto questo, più grande è \(n\), e maggiore sarà la complessità del modello risultante, in quanto maggiori saranno i parametri da stimare per poter apprendere e fare inferenza.
Andiamo adesso a vedere come applicare la teoria dei modelli di linguaggio nel contesto del classificatore Naive Bayes.
Il Naive Bayes multinomiale fa ricorso al più semplice dei modelli di linguaggio: il modello a unigramma. In particolare si utilizza un modello di linguaggio per ogni classe di interesse. Al fine di classificare il documento \(D\) possiamo sempre utilizzare il concetto della classe MAP trattato nella precedente lezione. Questa volta però otteniamo la seguente formula
\[C_{NB} = \underset{C_j \in C}{\text{argmax}} \,\, P(C_j) \cdot P(x_1, x_2, ..., x_m | C_j)\]
La principale differenza rispetto alla formula vista per il modello multivariato binomiale sta nel fatto che adesso abbiamo \(m\) features, ovvero una feature per ogni parola nel documento, e non una feature per ogni parola del vocabolario.
Se andiamo poi ad assumere la solita ipotesi di indipendenza Naive, otteniamo la seguente formula
\[C_{NB} = \underset{C_j \in C}{\text{argmax}} \,\, P(C_j) \cdot \prod_{i=1}^m P(x_i | C_j)\]
Anche così però il modello risulta essere troppo complesso: occorrenze diverse della stessa parola devono essere stimate separatamente. Per poter semplificare ulteriormente il calcolo, assumo un'altra ipotesi di indipendenza: si assume che la posizione delle parole è indipendente. Così facendo non ho più un Language Model, ma ho un Bag of Words Model.
Osservazione: Per token intendiamo le istanze delle parole nel testo. Ad ogni parola possiamo quindi associare più tokens. Per type invece intendiamo la parola presente nel dizionario. Per ogni parola abbiamo un solo type. Volendo utilizzare questa nomenclatura, il bag of words è un modello sui tokens, e non sui types.
Per effettuare il learning, ovvero per stimare le varie probabilità \(P(C_j)\) e \(P(x_k | C_j)\), nel classificatore di naives multivariato e multinomiale si procede come segue:
Le prior probabilities vengono stimate come prima, calcolano la frazione dei documenti del training set in ciascuna classe rispetto al numero di docs totali. In formula,
\[P(C_j) = \frac{| \text{Docs}_j | }{|D|}\]
Per le conditional probabilities invece, si procede andando a contare, per ogni classe \(C_j\) e per ogni parola \(x_k\) presente nel vocabolario, il numero di occorrenze della parola \(x_k\) in documenti della classe \(C_j\), che indicheremo con \(n_k\), e poi si calcola
\[P(X_k | C_j) = \frac{n_k + \alpha}{n + \alpha \cdot |V|}\]
dove \(n\) è il numero di parole totali presenti nella classe \(C_j\).
A seguire il relativo pseudocodice

Una volta effettuato il learning, possiamo classificare un documento \(D\) andandoci a calcolare il seguente argmax
\[C_{NB} = \underset{C_j \in C}{\text{argmax}} P(C_j) \cdot \prod_{i \in \text{pos}} P(X_i | C_j)\]
dove pos è l'insieme delle posizioni associate alle parole nel documento \(D\) che sono contenute nel dizionario.
La complessità temporale per il modello multivariato e multinomiale è la seguente, divisa per training time, ovvero il tempo necessario per l'apprendimento, e testing time, ovvero il tempo necessario per la classificazione:
Training Time:
\[O(|D| \cdot L_d + |C| \cdot |V|)\]
dove \(L_d\) è la lunghezza media dei documenti del training set \(D\).
Testing Time:
\[O(|C| \cdot L_t)\]
dove \(L_t\) è la lunghezza media dei documenti del test set.
Andiamo a sintantizzare i due modelli naive bayes che abbiamo introdotto prima:
Nel modello binomiale (bernoulli), abbiamo molte variabili, ciascuna delle quali rappresenta una proprietà associata ad una parola del dizionario. Queste variabili sono binomiali perché assumono valori in \(\{0, 1\}\), e se valgono \(1\) se la parola associata nel dizionario compare nel testo e \(0\) altrimenti.
L'ipotesi Naive in questo modello è che la presenza di una parola non influenza la presenza di altre parole. Così facendo features e eventi sono influenzati solo dalla categorie.
Questo modello è stato utilizzato nei primi anni 80 come modello di base per i primi motori di ricerca. In particolare la probabilità veniva utilizzata per riorganizzare con la tecnica chiamata relevance feedback i risultati ritornati dalle query. Analogia al bubble sort: più rilevanti salgono, meno rilevanti scendono.
\[P(x_w = 1 | C_j) = \text{frazione dei documenti del topic } C_j \text{ nei quali appare la parola } w \]
Nel secondo modello, il modello multinomial abbiamo una feature per ogni posizione (parola) di un documento. I valori che la feature può assumere sono le parole del vocabolario.
Abbiamo poi le seguenti assunzioni:
Naive Bayes Assumption: la presenza di una parola in una posizione non influenza le altre parole.
Second assumtpion: la probabilità dell'apparizione di una parola è indipendente dalla posizione della parola.
\[P(x_i = w | C) = P(x_j = w | C)\]
Dunque abbiamo una sola variabile multinomiale per ogni parola per documento
\[P(x_i = w | C_j) = \text{frazioni di volte in cui la parola } w \text{ appare in tutti i documenti della classe } C_j\]
Esempio di esecuzione.
Le collezioni di testi hanno un numero molto elevato di parole, e quindi di token, e quindi di features.
Nei modelli numerici in cui la stima dei parametri diventa molto delicata, all'aumentare del numero di features devo aumentare anche il size del training set. Rinunciando alle features che non siamo in grado di stimare bene, anche se perdiamo informazioni, riusciamo comunque a dare dei risultati più robusti, riducendo anche il training set. Questo processo è detto feature selection.
Nel contesto della text classification la feature selection può essere effettuata andando a "dimenticare" alcune parole. A tale fine possiamo utilizzare almeno i seguenti due approcci:
Hypothesis testing statistics: Utilizzo della statistica per capire, dato un training set, quanto sia utile dimenticarmi una variabile. Ad esempio è possibile utilizzare determinati test statistici, come il chi-squared test, per capire se una parola è fortemente associata ad una classe (o viceversa). Se tale associazione è molto debole, posso tranquillamente dimenticarmi la parola.
Information Theory: Concetto di mutua informazione: l'occorrere congiunto di parola e categoria rappresentano due eventi le cui distribuzioni di probabilità sono fortemente associate? Questa mutua informazione può essere applicata puntualmente a ogni coppia (parola, categoria), e ci permette di prendere le prime k parole e buttare via le altre per ottenere un dizionario di taglia k.
Most common terms: Una terza alternativa è quella di prendere i termini più comuni. Questa tecnica empirica è molto applicata in pratica.
La mutual information \(I(w, c)\) si comporta nel seguente modo:
Tende a a \(0\) al crescere dell'indipendenza deglie venti.
Tende ad aumentare tanto più quanto l'evento dell'uno influenza (in modo correlato) l'altro.
Tende a decrescere tanto più quanto l'evento dell'uno influenza (in modo contrario) l'altro.
Notiamo che la mutual information non è la cross entropy.
La mutual information può essere applicata nel seguente modo: per ogni categoria \(c\) mi prendo le \(k\) parole che hanno la mutual information più alta con \(c\). Per ottenere poi il vocabolario posso unire le \(|c| \cdot k\) parole tra loro.
Le tre tecniche menzionate possono (e sono) applicate e combinate assieme tra loro. Il processo della feature selection è quindi così descritto:
Si eliminano le parole funzioni e si lasciano i termini informativi.
Si prendono le parole più frequenti.
Si scremano le parole utilizzando la mutual information.
Dato che il modello binomiale ha un numero di variabili pari al numero di parole del dizionario, il process di feature selection risulta essere necessario per questo particolare modello statistico. Nel modello multinomiale invece, avendo una sola feature, la feature selection ci va ad eliminare dall'operativi del nostro modello alcune parole. Dal punto di vista statistico la feature selection ha un impatto meno importante.
NOTA BENE: Nel particolare caso in cui vogliamo applicare un classificatore Naive Bayes, vige l'ipotesi Naive, che ci dice che le parole sono indipendenti tra loro. Questo significa che non è utile cercare correlazioni tra termini durante la compilazione del vocabolario, in quanto nel modello di inferenza statistica le parole agiranno comunque in modo indipendente.
Nell'ambito del learning automatico produciamo modelli più o meno approssimati, il che significa che il modello sicuramente potrà sbagliare.
L'idea quindi è quella di valutare la qualità della classificazione fatta da un modello come la percentuale delle istanze di testing (o di training) in cui la classificazione proposta dal modello corrisponde a quella nota dal training set.
Per fare questa valutazione un possibile approccio è quello di separare i dati utilizzati per l'apprendimento in due insiemi: quelli di training, utilizzati per imparare il modello, e quelli di testing, utilizzati per valutare il modello. Questa separazione può essere eseguita più volte, per avere più numeri con cui lavorare.
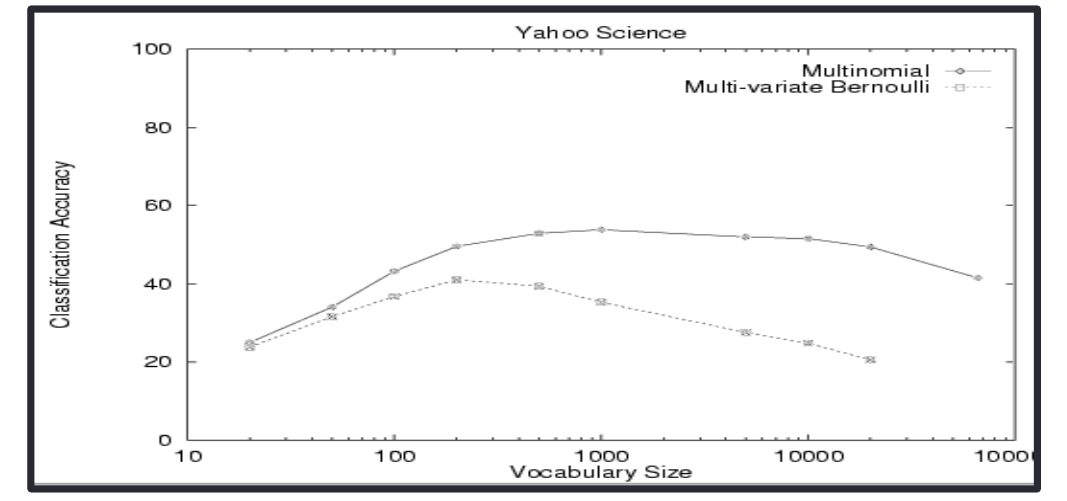
Come è possibile vedere dall'esempio, il modello multinomiale è più resistente di quello binomiale all'aumentare del size del vocabolario.
Per capire il size migliore del vocabolario possono essere utilizzate varie procedure sperimentali, tra cui troviamo la cross-validation, che consiste nell'utilizzare il training set per esplorare le possibili configurazioni del vocabolario e scegliere sulla basi di un'analisi media la configurazione del vocabolario che porta al modello "migliore".
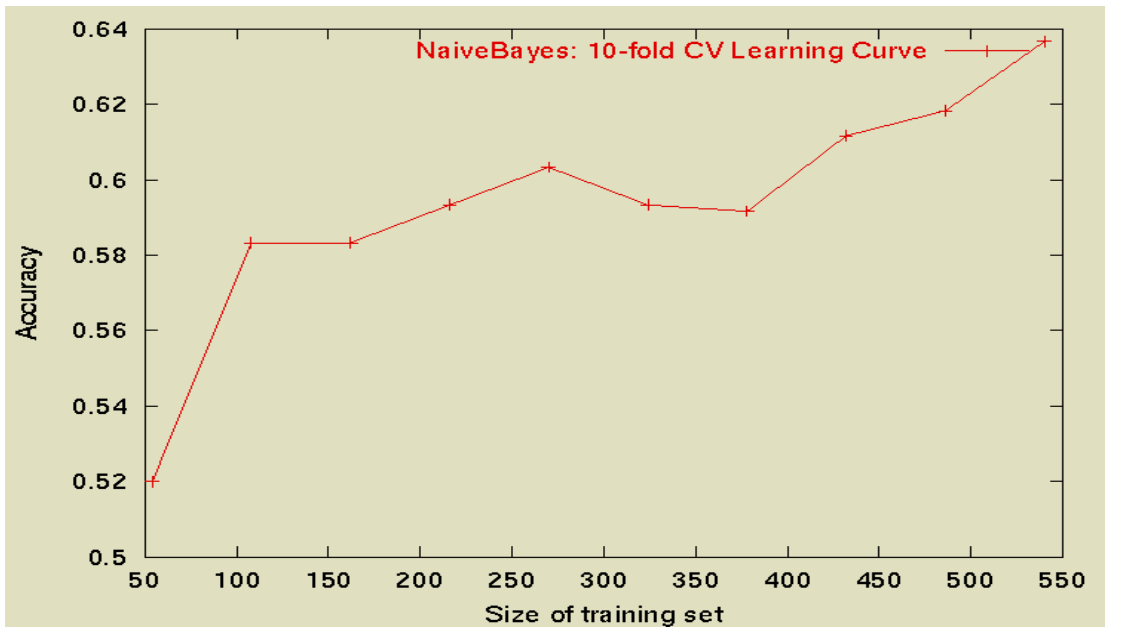
Notiamo anche che all'aumentare il numero di documenti del training set tendenzialmente aumentamo anche l'accuracy, anche se localmente potremmo avere dei minimi locali.
L'idea di questo sperimento è di classificare pagine web prese da un dipartimento di informatica nelle seguenti categorie
\[\text{student}, \;\;\; \text{faculty}, \;\;\; \text{course}, \;\;\; \text{project}, \;\;\; \text{peson}\]
Come training set sono state utilizzate \(5.000\) pagine etichettate manualmente. I risultati ottenuti sono stati i seguenti

Andando poi a vedere i dizionari che si sono costruiti per ogni classe (ovvero i vari modelli di linguaggio utilizzati dal classificatore), otteniamo la seguente situazione
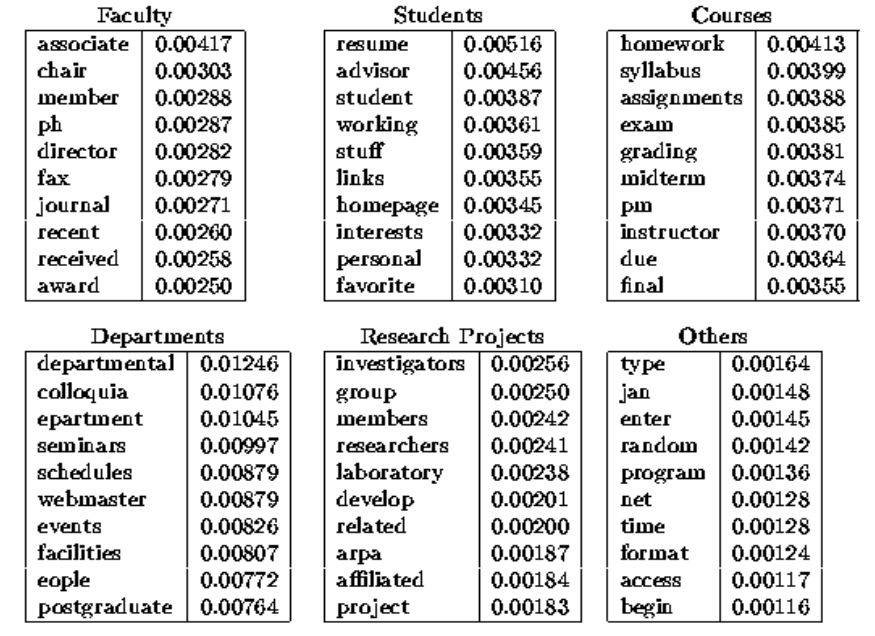
Tramite il classificatore quindi è possibile derivare dei dizionari di dominio.
Quando misureremo la qualità di una classificazione non ci basterà l'accuracy, che tende a mentire e dovremmo risolvere i seguenti problemi:
Cercare di capire, classe per classe, qual è il livello medio (baseline) della complessità del task. Queste baseline ci permettono di capire se il nostro sistema si sta comportando bene o male.
Studiare ogni singola classe a partire dalle categorizzazioni medie su ogni singola classe.
Un modello baseline per il problema dello spam di email è la most common category, che utilizza solamente la prior probability di ogni classe.
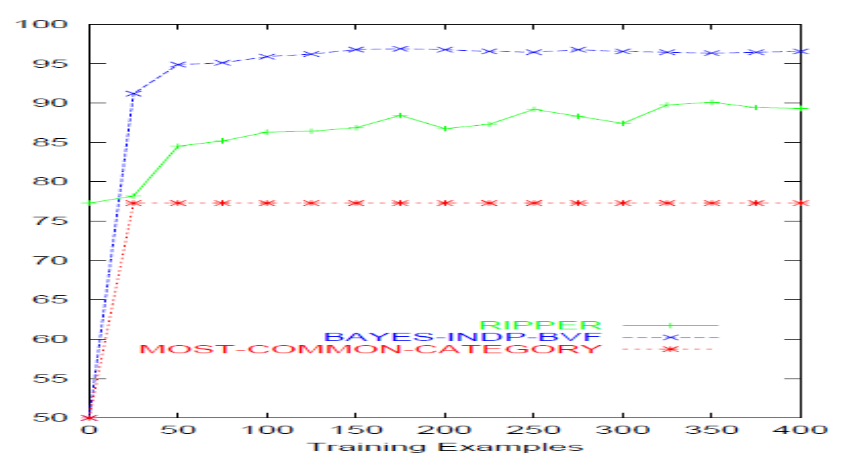
Notiamo che le assunzioni naive fatte nella trattazione del classificatore Naive Bayes non valgono in generale, e le abbiamo assunte solamente per semplificare il modello finale.
Consideriamo ad esempio l'ipotesi di indipendenza condizionale. Questa ipotesi è violata nel termine "Computer Science", in quanto con la nostra modellazione non possiamo considerare assieme queste parole ma le possiamo considerare solamente separate "Computer" e "Science".
Per quanto riguarda invece l'indipendenza posizionale, tale ipotesi non considera per niente le regole sintattiche di ogni linguaggio naturale e non.
In ogni caso, anche se le ipotesi su cui si basano non sono sempre rispettate, questi classificatori funzionano abbastanza bene, in quanto anche se stimiamo male le probabilità possiamo comunque avere delle inferenze corrette.
Anche se i classificatori Naive Bayes non competono con le reti neurali, essi presentano comunque una serie di proprietà utili e interessanti, tra cui troviamo le seguenti:
Robust to Irrelevant Features.
Very good in domains with many equally important features.
A good dependable baseline for text classification.
Optimal if the Independence Assumptions hold.
Very fast.
Low storage Requirements.
Machine Learning in Automated Text Categorization, Fabrizio Sebastiani.
A Comparison of Event Models for Naive Bayes Text Classification, Andrew McCallum and Kamal Nigam.
Machine Learning, Tom Mitchell.
A Re-examination of text categorization methods, Yiming Yang & Xin Liu.