WMR 07 - Machine Learning Metrics
Date:
Course Site: Web Mining e Retrieval (a.a. 2019/20)
Lecturer: Roberto Basili
Slides: ()
Table of Contents:
In questa lezione vediamo i meccanismi di valutazione delle prestazioni di algoritmi e sistemi di machine learning.
La valuazione è importante sia per misurare la qualità complessiva raggiungibile da un sistema di apprendimento e sia durante l'apprendimento, per selezionare il modello migliore tra tutti quelli possibili.
Considerando che tipicamente nei contesti in cui si applicano tecniche di learning non abbiamo a disposizione funzioni obiettivo analitiche, ne consegue che avere delle metriche che misurano la prestazione risulta fondamentale.
Le metriche di valutazione ci permettono di rispondere alle seguenti domande
Dato un sistema di ML, vogliamo capire se le prestazione del sistema sono "soddisfacenti".
Dato un insieme di diversi algoritmi/modelli, vogliamo capire quale di questi riesce a risolvere nel modo "migliore" un dato task.
Dato un modello, vogliamo capire come poter migliroare le performance del modello.
Abbiamo diverse tipologie di metriche a seconda del modello che stiamo analizzando. In particolare troviamo:
Performance Evaluation Metrics: vengono utilizzate principalmente per valutare i sistemi di classificazione e anche i sistemi di information retrieval. Il problema del retrieval è un particolare problema di regressione in cui ritorniamo un elenco ordinato di istanze.
Tuning and Evaulation Methods.
Error Diagnostics: cercano di modellare le ragioni che portano una misura prestazionale ad assumere un determinato valore rispetto agli errori effettuati.
Andiamo adesso a vedere le metriche utilizzate per valutare la performance di un modello di classificazione.
La prima cosa che possiamo fare per valutare le prestazioni di un sistema di classificazione è verificare quanto le classi predette utilizzando la funzione \(h()\) ottenuta dall'apprendimento coincidono con le classi effettive ottenute dalla funzione \(f()\) desiderata.
Per rappresentare il risultato della classificazione in modo da confrontare il valore effettivo con quello predetto di ciascuna istanza si utilizza la matrice di confusione \(C\). Se dobbiamo classificare \(n\) istanze in \(m\) classi, la matrice di confusione sarà una matrice \(m \times m\) definita come segue
\[c_{i, j} := \text{# elementi classe } i \text{ predetti come classe} j\]
Un esempio di matrice di confusione è la seguente
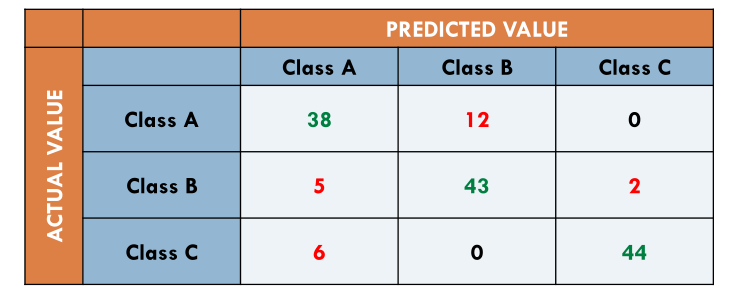
Notiamo che se sommiamo la diagonale della matrice di confusione otterremo il numero di istanze che sono state classificare correttamente.
Possiamo adesso definire la prima metrica di interesse, chiamata accuracy, definita come segue
\[\text{ accuracy } = \frac{\text{# classificazioni corrette}}{\text{# classificazioni}}\]
Un'altra metrica, duale a quella precedente, è chiamata error rate, ed è definita come segue
\[ \text{error rate } = \frac{\text{# classificazioni incorrette }}{\text{# classificazioni}} \]
Nel caso della matrice precedente troviamo
\[\begin{split} \text{ accuracy } &= \frac{38 + 43 + 44}{150} = 83.33 \% \\ \\ \text{ error rate } &= \frac{12 + 5 + 2 + 6}{150} = 16.67 \% \\ \end{split}\]
Osservazione: Tipicamente si utilizza l'accuracy per sistemi che hanno prestazioni molto lontane dal 100%, mentre si usa l'error rate per confrontare sistemi diversi quando l'errore è molto piccolo.
Q: L'accuracy viene o non viene utilizzata per i sistemi di di AI che elaborano informazioni sul web?
Notiamo che l'accuracy presenta delle problematiche quando le classi non sono bilanciate tra loro. Consideriamo ad esempio la seguente matrice di confusione associata alle performance di uno spam detector.
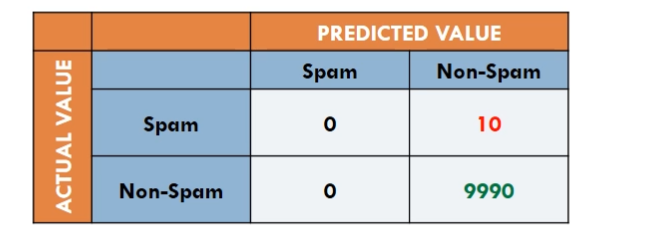
Se nel nostro dataset solo una piccola porzione dei messaggi è di spam, allora mettendo tutto a non-spam in modo brute-force riusciamo comunque ad avere una percentuale di accuracy molto alta. Notiamo infatti che l'accuracy di questo classificatore è pari a
\[\text{accuracy} = \frac{9990}{10000} = 99.9\%\]
Queste problematiche derivano dal fatto che l'accuracy è una misura globale, e non prende in considerazione le performance nel contesto delle singole classi.
Consideriamo una classe \(C\). Volendo definire delle metriche che ci permettano di stabilire le performance di un classificatore rispetto alla classe \(C\) otteniamo le seguenti metriche
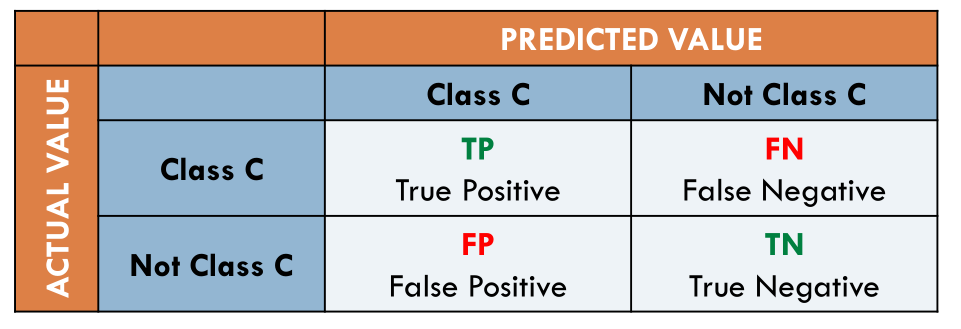
Volendo descriverle con più dettaglio abbiamo,
True Positive: Numero delle istanze che facevano parte della classe \(C\) e che sono state classificate nella classe \(C\).
True Negative: Numero delle istanze che non facevano parte della classe \(C\) e che non sono state classificate nella classe \(C\).
False Negative: Numero delle istanze che facevano parte della classe \(C\) e che non sono state classificate nella classe \(C\).
False Positive: Numero delle istanze che non facevano parte della classe \(C\) e che sono state classificate nella classe \(C\).
Notiamo quindi che rispetto alla classe \(C\) il classificatore sbaglia nei casi \(\text{FP}+\text{FN}\), ed è corretto nei casi \(\text{TP}+\text{TN}\). Utilizzando queste quantità siamo poi in grado di definire nuove metriche, tra cui troviamo:
Precision: Calcola la percentuale di istanze effettivamente positive tra tutte quelle classificate come positive. Formalmente,
\[\text{precision } := \frac{TP}{TP + FP}\]
Più preciso è un sistema, e minore saranno le volte che sbaglia quando classifica una istanza come facente parte della classe \(C\).
Recall: Calcola la percentuale di istanze classificate come positive rispetto a tutte le istanze effettivamente positive. Formalmente,
\[\text{recall } := \frac{TP}{TP + FN}\]
Più la recall (copertura) è alta, e più il nostro sistema è in grado di trovare e classificare correttamente la maggior parte delle istanze in C.
Notiamo che la precision e la recall sono metriche contrastanti l'un l'altra. Tipicamente infatti più piccola è la recall e più alta la precisione può diventare, in quanto sto restringendo il campo di analisi rispetto all'appartenenza della classe C. Viceversa, più piccola è la precisione, e più alta la recall può diventare, in quanto posso semplicemente classificare come C anche documenti di cui non sono molto sicuro.
Per avere una misura che cerca di combinare le due metriche, al posto di effettuare la semplice media, si calcola la media armonica tra le due quantità, che prende il nome di F-measure ed è definita come segue
\[\text{F1} = \frac{2 \cdot \text{precision} \cdot \text{recall}}{\text{precision} + \text{recall}}\]
La media armonica ci permette di avere una visione più pessimistica rispetto alla precision e alla recall.
Osservazione: Viene indicata con \(F1\) per rappresentare il fatto che nella F-measure precisione e recall pesano nello stesso modo. Si possono poi avere delle metriche che non danno lo stesso peso alla precision e alla recal. Ad esempio, nel caso degli antivirus, i falsi negativi (virus che non vengono scoperti) sono "peggio" rispetto ai falsi positivi (programmi normali che vengono interpretati come virus).
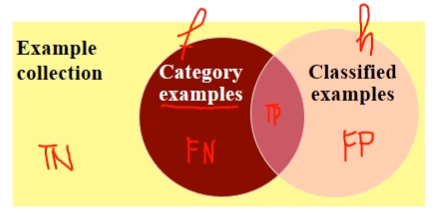
È possibile descrivere i concetti di precision e recall anche utilizzando la teoria degli insiemi. Consideriamo infatti il seguente diagramma di Venn.
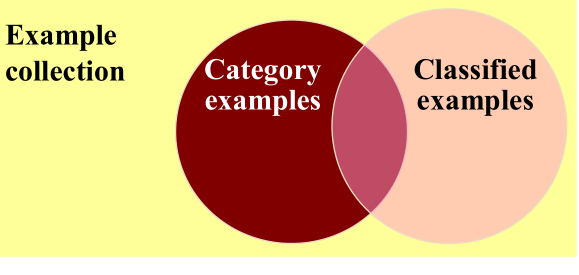
Possiamo associare ad ogni zona del diagrama un valore tra TP, TN, FP, e FN nel seguente modo:
Consideriamo il seguente quadrato in cui possono variare i valori delle metriche di precision e recall, che essendo delle percentuali possono singolarmente variare nell'intervallo \([0,1]\).
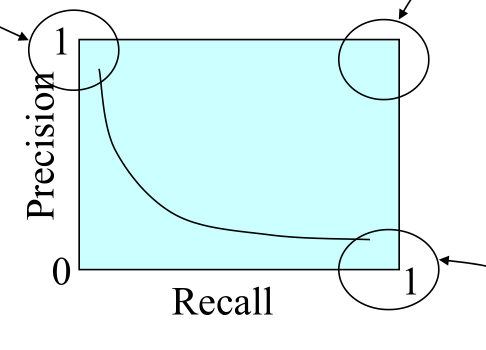
Andiamo quindi a descrivere i casi limite interessanti di questo quadrato a seconda dei valori di precision e recall:
(0, 1): Caso di precision massima in cui tutti i membri classificati della classe in questione appartengono effettivamente alla classe ma perdiamo molte istanze che appartengono alla classe.
(1, 0): Caso di recall massima in cui riesco a prendere la maggior parte delle istanze della classe \(C\), ma che classifico come \(C\) anche tante altre istanze.
(1, 1): Caso ideale ed impossibile da ottenere.
Il nostro obiettivo è quindi quello di aumentare la distanza dall'origine della curva di trade-offs tra precisione e recall.
Consideriamo di avere una sola classe da classificare.
La prima metrica di interesse per combinare la precision e la recall è quello che viene chiamato il break-even point (BEP), definto come il punto nella curva precision-recall in cui la precision e la recall assumono lo stesso valore.
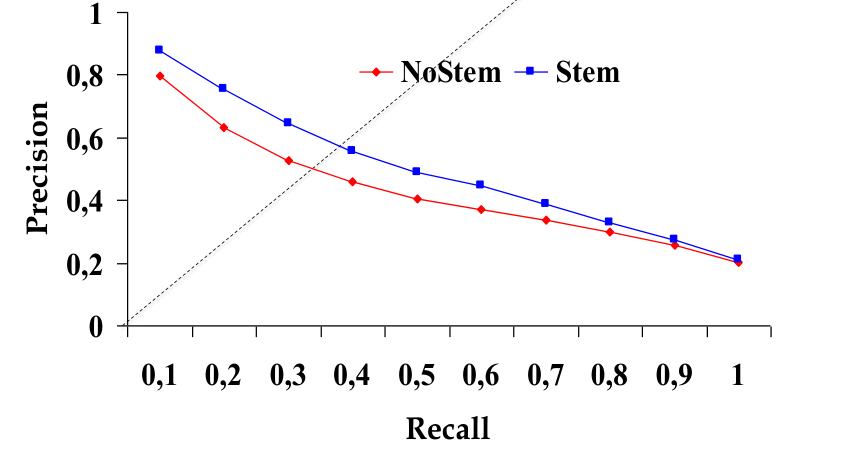
Notiamo che, anche se non sempre il break-even point è un valore di soglia, ovvero un valore effettivamente misurabile, per ottenerlo possiamo prima calcolare la curva precision-recall del nostro sistema andando ad interpolare i vari valori di soglia ottenuti, e successivamente calcolare il punto in cui \(\text{precision}=\text{recall}\).
Tramite il BEP siamo in grado di stabilire quanto la precision-recall curve si avvicina al punto di coordinata \((1, 1)\), che è il punto ideale a cui puntiamo.
Osservazione: Nel grafico visto prima stiamo confrontando due sistemi che applicano lo stesso algoritmo ma con diverse rappresentazioni: nel sistema con la curva blu le parole vengono pre-processate tramite una procedure che prende il nome di stemming, mentre nel sistema con la curva rossa le parole non vengono pre-processate.
Per cercare di combinare la precision e la recall in un unico valore abbiamo già introdotto la F-measure. Altre possibili metriche sono:
minimo
\[\text{min}(p, r)\]
massimo
\[\text{max}(p, r)\]
media aritmetica
\[\text{arithM}(p, r) = \frac{p + r}{2}\]
media geometrica
\[\text{geomM}(p, r) = \sqrt{p \cdot r}\]
media armonica
\[\text{harmM}(p, r) = \frac{2}{p^{-1} + r^{-1}}\]
A seguire un grafico in cui vengono mostrate le curve delle varie performance al variare della precision, con la recall fissata al 70%.
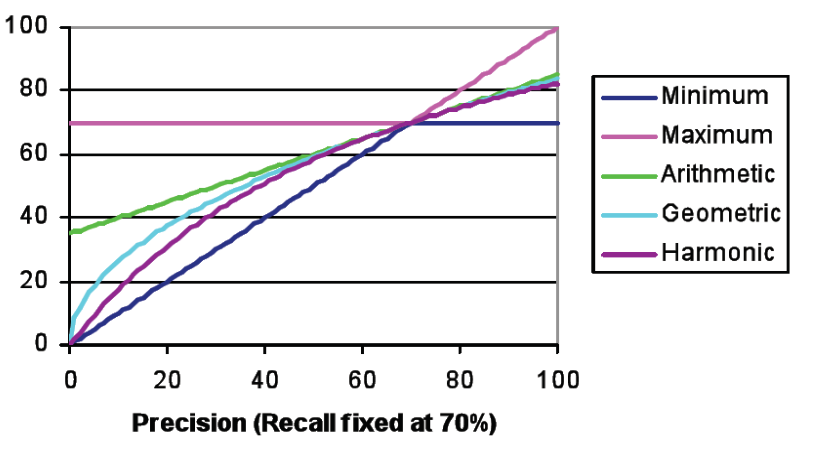
Avendo più classi a disposizione, possiamo definire la precision e la recall per ciascuna delle classi \(C_i\) su cui dobbiamo risolvere il problema della classificazione. A questo punto ci dobbiamo chiede come possiamo combinare le varie metriche di precision e recall per ciascuna classe per ottenere un indice di performance globale.
Un modo iniziale per combinare la precisione e la recall delle varie classi è tramite un semplice macro averaging,
Macro precision
\[\text{MPrecision} = \sum\limits_{i = 1}^n \text{Precision}_i\]
Macro recall
\[\text{MRecall} = \sum\limits_{i = 1}^n \text{Recall}_i\]
Da queste poi possiamo definire la macro F1 measure, definita come la media armonica della macro precision (MP) e della macro recall (MR)
Macro F1 measure
\[\text{MF}_1 = \frac{2 \cdot \text{MPrecision} \cdot \text{MRecall}}{\text{MPrecision} + \text{MRecall}}\]
todo.
Q: BEP e micro definizioni.
R: Il BEP viene dall'economia e definisce il punto in cui un'azienda riesce a coprire i costi utilizzando il profitto.
La micro-precision e micro-recall vengono utilizzate quando si hanno più classi.
La micro-precision è la precisione delle decisioni individuali, mentre la macro-precision è la precisione rispetto alle singole classi. La micro-precision è quindi più precisa, specialmente rispetto alla dimensione della classe, in quanto nella macro-precision si assume una prior probability uniforme rispetto a tutte le classi.
Le metriche non servono solamente per validare la performance di un sistema di machine learning una volta che questo è stato completamente definito.
Le metriche sono importanti anche perché ci offrono degli strumenti di comparazione tra sistemi e algoritmi diversi. Ad esempio una volta che fissiamo la famiglia in cui si trova il modello desiderato, a seconda dei parametri scelti avremmo diverso modelli che si comporteranno in modi diversi. Tramite delle metriche di tuning possiamo quindi valutare le prestazioni dei vari modelli in modo tale da scegliere la parametrizzazione che ci permette di ottenere i migliori risultati.
L'apprendimento automatico è quindi la ricerca, nello spazio dei parametri, delle configurazioni che consentono alla funzione h() che stiamo costruendo di funzionare in modo ottimo. Il processo di learning si basa sul trovare delle sequenze di modelli che aumentano sempre di più le prestazioni ottenute.
Le tecniche di cross-validation permettono di utilizzare i dati di training nel modo migliore possibile per addestrare il sistema. Notiamo infatti che una volta ottenuto il modello, le metriche di performance devono essere calcolate rispetto a dei dati nuovi, e non a quelli utilizzati per il training. Necessitiamo quindi di utilizzare delle procedure che prendono il dataset iniziale e lo dividono in due sotto-datasets: quello di training, utilizzato per addestrare il modello, e uno di testing, utilizzato per valutare il modello.
Il processo della cross-validation è una procedura del enere, e consiste nei seguenti steps:
Dataset splitting: L'insieme dei dati annotati vengono splittati in due sottoinsieme di dati: un sottoinsieme chiamato training set, che verrà utilizato per addestrare il sistema, e un sottoinsieme chiamato testing set, che verrà utilizzato per calcolare le metriche di performance del sistema. Un tipico split è caratterizzato dal 70% del dataset iniziale per il training set, e il restante 30% per il testing set.
Learning phase: Si utilizza un algoritmo di apprendimento che prende in input il training set e produce un modello che cerca di risolvere il task di interesse. Il modello ottenuto è chiamato modello della decisione.
Testing the model: Si applica il modello ottenuto nel passo precedente ai dati contenuti nel test set, senza però considerare l'annotazione dei dati del test set. Una volta applicato il modello, confrontiamo le decisioni prese dal modello rispetto alle annotazioni effettive dei dati del test set e calcoliamo le metriche di perfmrance.
Quando i dati sono limitati, un singolo processo di valutazione potrebbe non essere abbastanza significativo, in quanto data la limitatezza del testing set potremmo beccare una porzione di dati su cui performiamo bene anche se in realtà il modello è carente in altri contesti.
Per gestire la problematica menzionata prima si effettua del sampling (campionamento), ovvero l'intero processo viene ripetuto rispetto a diversi split del dataset.
Questo processo è detto N-fold cross validation, e funziona nel seguente modo: Inizialmente divido il dataset etichettato in \(N\) sottoinsiemi di uguale dimensione. A questo punto itero un processo di valutazione per \(N\) volte: ad ogni round scelgo un particolare sottoinsieme del dataset e lo utilizzo come test set, mentre i restanti \(n-1\) vengono utilizzati per il training.
Le metriche che vengono calcolate in ciascun round vengono poi combinate assieme tramite dei calcoli di media.
L'hand-fold cross-validation si oppone alla tecnica dello split fisso, in quanto ci permette di vedere tutti i dati e ci da quindi più informazioni rispetto alla valutazione
La maggior parte degli algoritmi di apprendimento dipende da determinati parametri. Tra quelli che abbiamo visto infatti abbiamo:
kNN: Il parametro è il numero k che specifica quanti vicini devo considerare intorno al punto prima di calcolare la classe.
Rocchio: I parametri sono i pesi delle parole \(w_i\).
Naive Bayes: I parametri sono le probabilità condizionate p(w_i | c_j) e le probabilità a priori p(c_j).
Dato che non c'è a prima vista un parametro ottimale, per scegliere il parametro migliore possibile bisogna effettuare un processo di tuning. Il processo di tuning consiste di:
Definire un insieme di configurazioni possibili.
Testare ciascuna configurazione deve essere testata.
Scegliere la configurazione che dà i migliori risultati.
Il processo completo di ML è descritto dal seguente diagramma
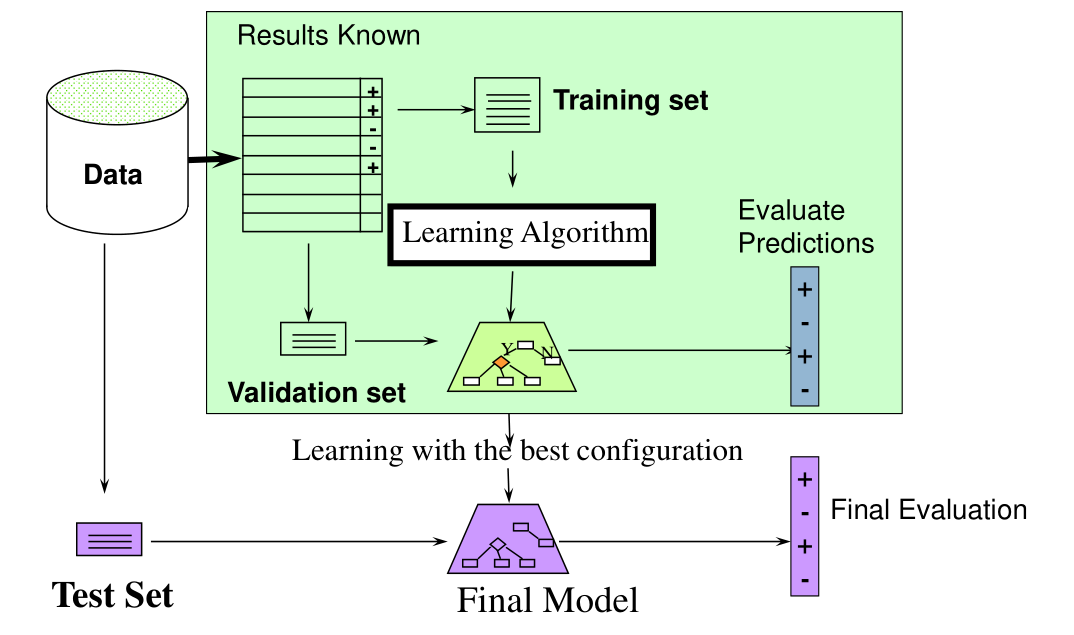
dove l'area del rettangolo verde rappresenta la fase di training, in cui i dati di testing sono utilizzati per fare tuning del modello e per scegliere così facendo il modello migliore. Il processo di training può essere iterativo, nel senso che può iterare più volte in sé stesso prima di arrivare al modello finale. Solo una volta che il modello finale è stato selezionato è possibile effettuare la validazione finale.
Notiamo quindi che la tecnica n-fold cross-validation può essere utilizzata in due modi diversi:
All'interno dell'addestramento, per ottenere il modello.
Dopo aver addestrato il modello, per ottenere il campionamento del test set a partire dal dataset originale e ottenere così più valutazioni, che posso poi accorpare in valori di media.
In particolare posso procedere come segue:
Divido il dataset originale in 5 sottoinsiemi, e scelgo una per fare test set e le altre quattro per fare training set.
A partire da queste quattro scelgo un particolare sottoinsieme come validation set e addestro il sistema con una parametrizzazione \(w_0\). Poi utilizzo come validation set un altro sottoinsieme, e via dicendo fino a quando ho un valore di media del comportamento del sistema con parametrizzazione \(w_0\).
Poi scelgo un altro sottoinsieme per fare test set e le altre quatto per fare training set, e ripeto il passo precedente questa volta però con un parametro diverso \(w_1\).
Posso ripetere questo per \(N\) volte, ottenendo \(N\) valori diversi, ciascuno dei quali descrive in media come si comporta il sistema con una determinata parametrizazione. A questo punto posso scegliere la parametrizzazione "migliore" (magari quella in cui il sistema si comporta meglio in media).
Una volta finalizzato il tutto posso addestrare il sistema su training e validation e tirare fuori con il test set la validazione finale del sistema.
In generale posso applicare due tecniche:
Posso confrontare tutti i parametri con tutti i test sets.
Prendere i parametri che vanno molto meglio di altri su almeno un fold.
Osservazione: Siamo disposti ad investire nella complessità del processo di addestramento in quanto il processo di addestramento deve essere eseguito una sola volta, mentre il modello finale potrebbe essere utilizzato tante volte.
Se il dominio della parametrizzazione si trova nella retta reale, devo scegliere delle tecniche che mi permettono di esplorare lo spazio di variabilità del parametro in modo intelligente attraverso delle tecniche di analisi numerica.
Consideriamo la collezione di documenti di Reuters.
Volendo utilizzare l'algoritmo di Rocchio per effettuare la classificazione, ricordiamo che il contributo della parola \(w\) nella categoria \(C_i\) era data dalla seguente espressione
\[\Omega(w, C_i) = \max\Bigg\{0, \;\;\; \frac{\beta}{|T_i|} \cdot \sum_{d \in T_i} \omega_w^d - \frac{\gamma}{|\overline{T}_i|} \cdot \sum_{d \in \overline{T}_i } \omega_w^d\Bigg\}\]
dove,
\(T_i\) è l'insieme dei documenti presenti nel training set e classificati come far parte della categoria \(C_i\)
\(\overline{T}_i\) è l'insieme dei documenti presenti nel training set che non fanno parte di \(C_i\).
Ora, al posto di utilizzare dei valori fissi per \(\beta\) e \(\gamma\), l'idea è quella di avere dei valori parametrizzati alla categoria \(\beta_i\) e \(\gamma_i\). Dividendo poi per \(\beta_i\) possiamo ottenere un solo parametro \(\rho_i = \gamma_i/\beta_i\) che varia a seconda della categoria considerata \(C_i\).
Osservazione: Nelle prime applicazioni di Rocchio si era visto che \(\beta > \gamma\) di un fattore $4, 16, ...$.
Il dataset utilizzato è formato da \(12902\) documenti rappresentati in un fixed-split con \(9603\) documenti per training e \(3299\) documenti per testing.
Facendo variare gamma rispetto alla categoria degli acquisti otteniamo il seguente grafico
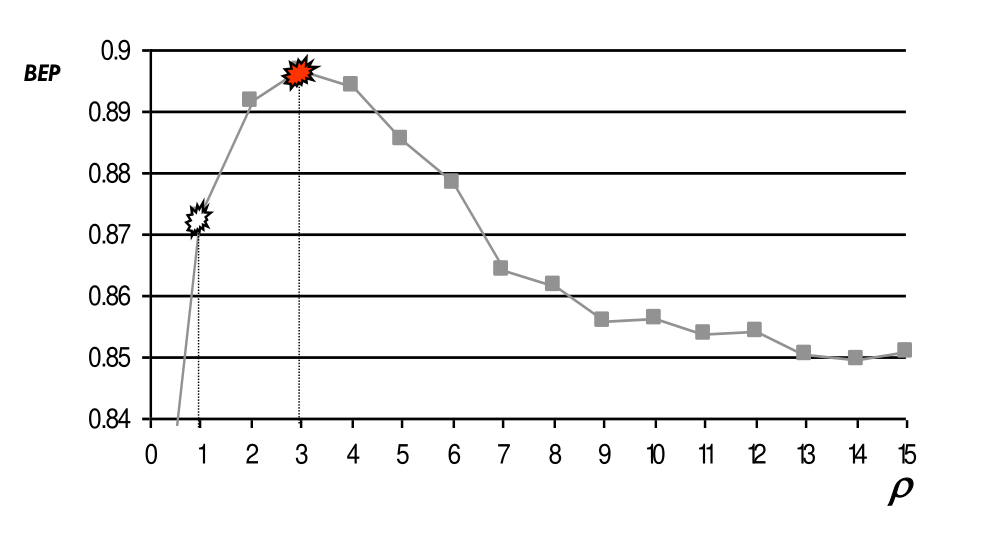
Osservazione: Una oscillazione del 5% tra 85% e 90% non è la stessa cosa rispetto ad una oscillazione del 5% tra 10 e 15%.
Andando a cambiare la classe osservata cambia anche il relativo grafico
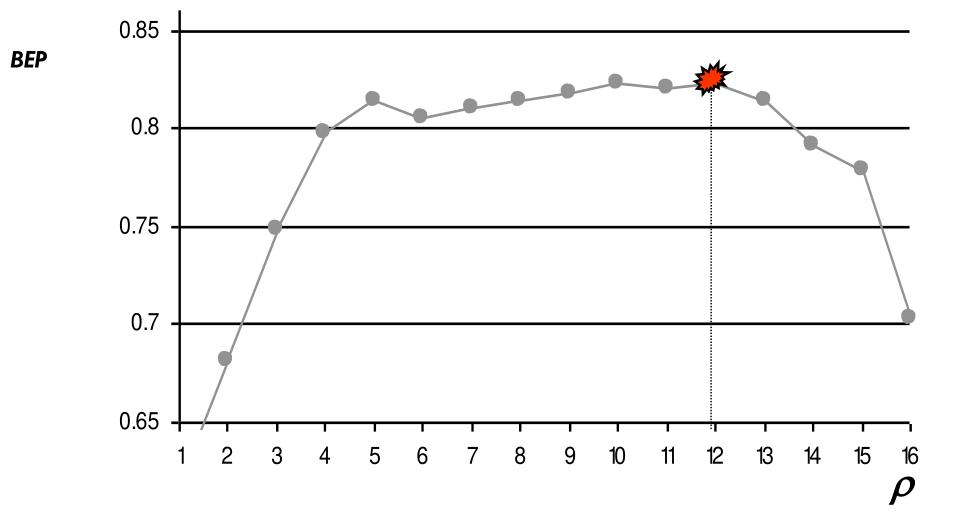
Per cercare di capire il miglior valore \(\rho\) posso procedere nel seguente modo:
Utilizzo il \(30\%\) del training set come validation set.
Per ogni \(\rho \in [0, 30]\)
Addestro il sistema nella parte rimanente del training set.
Misuro il BEP (Break-Even-Point) rispetto al validation set.
Prendo il valore \(\rho\) associato al BEP più alto.
Addestro nuovamente il sistema sull'interno train set a partire dal \(\rho\) scelto prima.
Valuto il sistema utilizzando il test set.
I lavori che hanno utilizzati questo dataset sono:
Joachmins, 1998.
Lam and Ho, 1998.
Dumais et al, 1998.
Li Yamanishi, 1999.
Weiss et ai, 1999.