WMR 09 - Lab I (Decision Trees + Weka)
Lecture Info
Date:
Course Site: Web Mining e Retrieval (a.a. 2019/20)
Lecturer: Danilo Croce.
Slides: ()
Table of Contents:
Nella seguente lezione abbiamo discusso un algoritmo di apprendimento automatico che costruisce un albero decisionale e infine abbiamo fatto vedere il took weka.
1 The Problem
Vogliamo risolvere un problema di classificazione in cui abbiamo un insieme di istanze, che rappresentano dipendenti di una società, e per ogni istanza una serie di attributi. Vogliamo utilizzare i vari attributi dei dipendenti per capire in quale livello della gerarchia possono essere assegnati.
A tale fine possiamo applicare delle tecniche di machine learning, che utilizzano i dati per addestrare il modello. Come al solito non dobbiamo solo tener contro della fase di addestramento, ma anche di quella del testing.
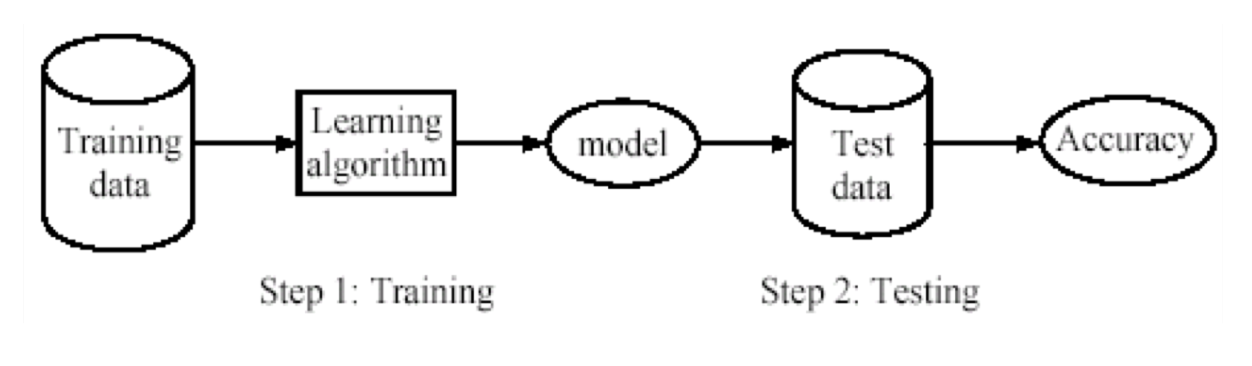
Osservazione: Tipicamente nelle challenge che si organizzano nel contesto del machine learning ai partecipanti vengono dati solamente i dati del training set. Una volta addestrati i vari modelli vengono poi testati utilizzando i dati del test set, e il modello con le performance migliore è il migliore.
Il dataset con cui lavoriamo è il seguente
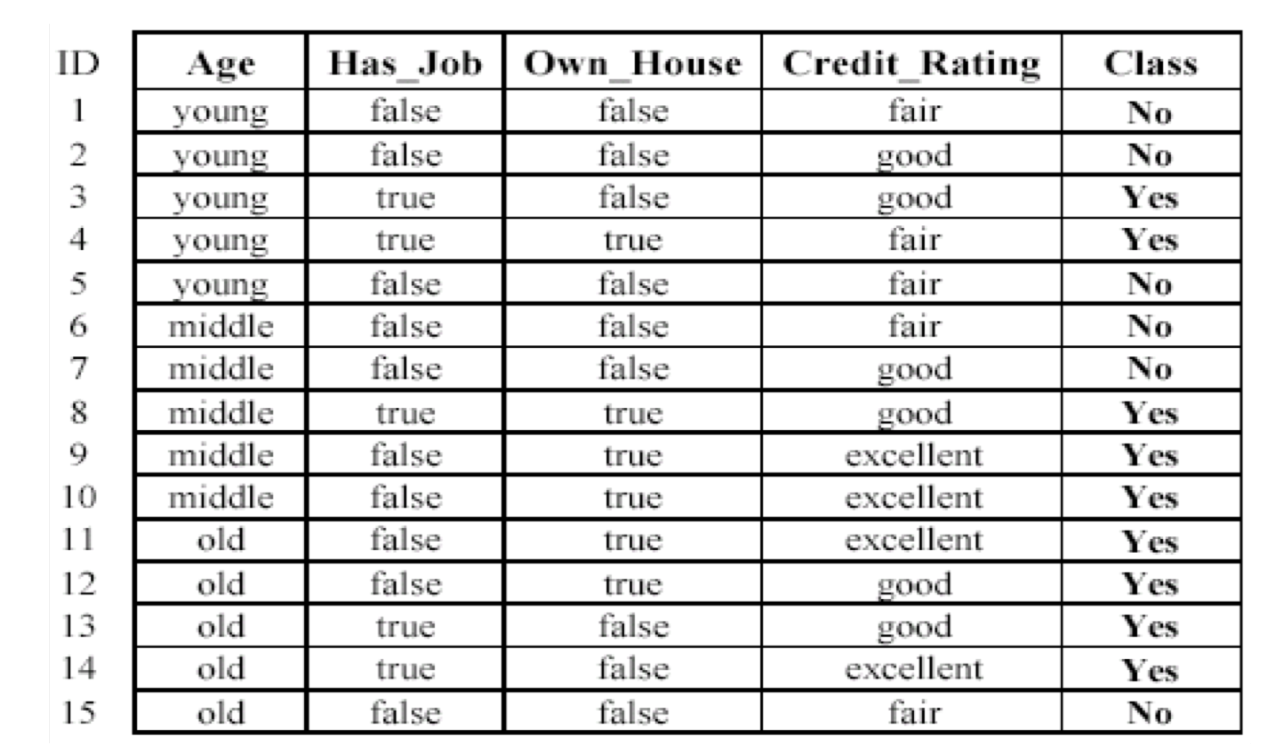
e la classe che vogliamo apprendere è la classe delle persone a cui è garantino il loan (prestito).
2 Decision Tree (J48)
Oltre ai modelli già visti, tra cui troviamo Bayesian Classifier, kNN, Rocchio, abbiamo un'altra famiglia di modelli, detti Boolean Functions, o alberi delle decisioni.
Questi modelli sono detti "booleani" in quanto effettuano un'analisi booleana dei singoli attributi: per associare un istanza ad una classe si analizzano attributo per attributo, e a seconda del range in cui ricadono i vari attributi si avrà una decisione diversa.
Il vantaggio principale dei decision trees, che gli ha permesso di non finire nel dimenticatoio, anche se sono meno efficienti da addestrate e sono meno performanti di tecniche come le reti neurali, è il fatto che sono trasparenti da un punto di vista epistemologico, ovvero che non solo vediamo la decisione finale presa dal modello, ma vediamo anche la catena di inferenze che ha portato il modello a prendere quella particolare decisione. Sapere come il modello effettua le sue decisioni può essere necessario quando dobbiamo certificare la decisione presa in contesti legali/sociali.
Noi vogliamo utilizzare proprio uno di questi modelli booleani per risolvere il nostro problema di classificazione. Il problema è che possiamo avere vari tipi di decision trees.
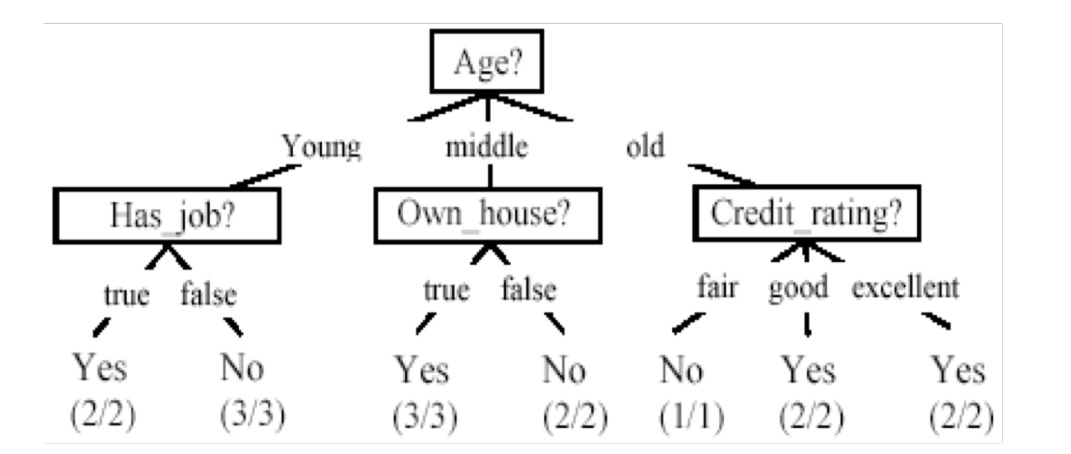
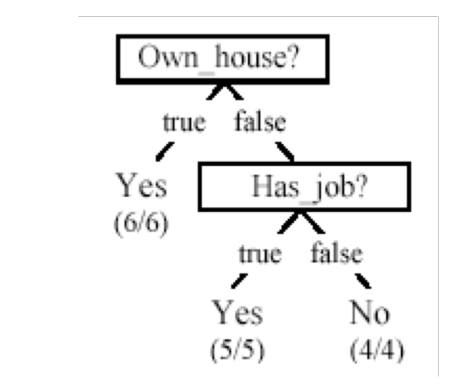
Ci dobbiamo quindi chiedere: fissato un decision tree, come faccio a valutarlo? Rispetto a cosa posso dire se un albero è meglio o peggio di un altro albero? Notiamo ad esempio che è possibile definire un albero più piccolo di quello precedente
Osservazione: È stato dimostrato da Vladimir Naumovich Vapnik che "semplice è meglio", nel senso approssimato che più semplice è il modello che sto utilizzando e più riesco a diminuire l'errore rispetto ad istanze future. Detto questo, nel nostro caso particolare trovare l'alberto più "semplice" però è un problema NP-hard, e quindi dobbiamo necessariamente utilizzare delle euristiche.
2.1 Basic Idea
Per costruire il nostro decision tree cercheremo di analizzare i vari attributi in modo da prendere quello che meglio separa le istanze rispetto all'appartenenza alle varie classi. Questo passo è poi ripetuto ricorsivamente fino ad ottenere la separazione a grana fine delle istanze nelle varie classi.
In questo contesto torna utile il concetto di purità: un sottoinsieme di dati è detto puro se tutte le istanze del sottoinsieme appartengono alla stessa classe.
Idealmente vorremmo infatti splittare i dati in sottoinsiemi puri, in modo da rendere banale la decisione di classificazione. Per fare questo si utilizza la seguente euristica: si prende l'attributo con la massima information gain e si dividere il dataset rispetto ai valori di quell'attributo.
2.2 Entropy
Ricordiamo che l'entropia nel contesto dell'information theory ci permette di misurare l'incertezza, o il contenuto informativo, di un dato evento.
Consideriamo un training set \(D\), e sia \(m = |C|\) il numero delle classi target. Possiamo definire \(X\) come la v.a. che rappresenta la classe di un elemento estratto a caso dal training set \(D\). Notiamo che \(X\) è una v.a. discreta con una sua densità descrita ottenuta dai valori \(P(c_1), \ldots, P(c_m)\), dove
\[P(c_i) = \text{probabilità che l'elemento estratto appartiene alla classe} c_i\]
A questo punto possiamo calcolare l'entropia di \(X\) come segue
\[H(X) = - \sum\limits_{j = 1}^{m} P(c_j) \log_2{P(c_j)}\]
Consideriamo i seguenti esempi in un contesto di classificazione binaria in cui \(C = \{\text{Positive}, \text{Negative}\}\).
Se il nostro dataset \(D\) ha il \(50\%\) degli esempi nella classe \(\text{Positive}\) e il restante \(50\%\) nella classe \(\text{Negative}\), allora troviamo
\[H(X) = - 0.5 \cdot \log_2{0.5} - 0.5 \cdot \log_2{0.5} = 1\]
Se il nostro dataset \(D\) ha il \(20\%\) degli esempi nella classe \(\text{Positive}\) e il restante \(80\%\) nella classe \(\text{Negative}\), allora troviamo
\[H(X) = - 0.2 \cdot \log_2{0.2} - 0.8 \cdot \log_2{0.8} = 0.722\]
Se il nostro dataset \(D\) ha il \(100\%\) degli esempi nella classe \(\text{Positive}\) e il restante \(0\%\) nella classe \(\text{Negative}\), allora troviamo
\[H(X) = - 1 \cdot \log_2{1} - 0 \cdot \log_2{0} = 0\]
2.3 Construction
L'idea per la costruzione del nostro decision tree consiste nel calcolare l'entropia del dataset originale per avere una baseline che verrà poi utilizzata per capire se l'attributo preso in considerazione permette di splittare il dataset andando a ridurre l'entropia delle parti oppure andandola ad aumentarla.
Observation: In generale per misurare le performance di un sistema di apprendimento automatico è di fondamentale importanza avere una baseline che ci permette di misurare la difficoltà del task affrontato.
Per fare questo calcolo iniziale posso utilizzare le probabilità a priori \(P(c_j)\) stimate tramite una semplice calcolo della frequenza. Nel nostro caso ad esempio ho due classi, di cui
\[\begin{split} P(C_\text{No}) &= \frac{6}{15} = \frac{2}{5} \\ P(C_\text{Yes}) &= \frac{9}{15} = \frac{3}{5} \\ \end{split}\]
La costruzione poi continua andando a selezionare ogni feature e partizionando il dataset rispetto al valore assunto da quella feature. Per calcolare la qualità di tale partizionamento calcolo l'entropia totale di questa scelta utilizzando l'equazione a seguire
\[H_{A_i}(D) = \sum\limits_{j = 1}^v \frac{|D_j|}{|D|} H(D_j)\]
dove \(A_i\) è l'attributo preso in considerazione, \(v\) è il numero di valori distinti assunti da tale attributo, e \(D_1, D_2, \ldots, D_v\) sono i sottoinsiemi della partizione ottenuta.
Una volta che ho fatto questo per tutte le features seleziono la feature che minimizza l'entropia totale, o, equivalentemente, che massimizza l'information gain (mutual information), dove l'information gain è definito nel seguente modo
\[IG(D, A_i) = H(D) - H_{A_i}(D)\]
ovvero è la differenza tra la prior entropy e l'entropy rispetto all'attributo selezionato.
2.3.1 Example
Prendendo in considerazione il dataset di prima, abbiamo che la prior entropy è calcolata come segue
\[H(D) = -\frac{6}{15}\log_2{\frac{6}{15}} - \frac{9}{15}\log_2{\frac{9}{15}} = 0.971\]
Se poi partizioniamo rispetto all'attributo \(\text{Age}\) otteniamo
\[H_{\text{Age}}(D) = \frac{5}{15}H(D_1) + \frac{5}{15}H(D_2) + \frac{5}{15} H(D_3) = 0.888\]
dove,
\[\begin{split} H(D_1) &= -\frac{3}{3+2} \cdot \log_2{\Big(\frac{3}{3 + 2}\Big)} -\frac{2}{3+2} \cdot \log_2{\Big(\frac{2}{3 + 2}\Big)} = 0.971 \\ H(D_2) &= -\frac{2}{3+2} \cdot \log_2{\Big(\frac{3}{3 + 2}\Big)} - \frac{3}{3+2} \cdot \log_2{\Big(\frac{3}{3 + 2}\Big)} = 0.971 \\ H(D_3) &= -\frac{1}{1+4} \cdot \log_2{\Big(\frac{1}{1 + 4}\Big)} - \frac{4}{1+4} \cdot \log_2{\Big(\frac{4}{1 + 4}\Big)} = 0.722 \\ \end{split}\]
Invece, se partizioniamo rispetto all'attributo \(\text{House}\) otteniamo
\[H_{\text{House}}(D) = -\frac{6}{15}H(D_1) - \frac{9}{15}H(D_2) = -\frac{6}{15} \cdot 0 + \frac{9}{15} \cdot 0.918 = 0.551\]
Calcolando l'information gain per i vari attributi ottengo quindi la seguente situazione
\[\begin{split} \text{gain}(D, \text{Age}) &= 0.971 - 0.888 = 0.083 \\ \text{gain}(D, \text{House}) &= 0.971 - 0.551 = 0.420 \\ \text{gain}(D, \text{Job}) &= 0.971 - 0.647 = 0.324 \\ \text{gain}(D, \text{Credit}) &= 0.971 - 0.608 = 0.363 \\ \end{split}\]
Dato che l'information gain è massimo rispetto l'attributo \(\text{House}\), scelgo tale attributo come radice del mio albero e itero nuovamente il procedimento.
2.4 Discretization of Features
Osserviamo che per applicare queste funzioni di suddivisione gli attributi devono necessariamente essere categoriali.
Se abbiamo a che fare con features numeriche quindi, dobbiamo quindi effettuare un processo di discretizzazione delle features. Andandoli a discretizzare è possibile qindi utilizzare la stessa features più volte a vari livelli del nostro decision tree.
2.5 Algorithm
L'algoritmo finale è quindi un algoritmo greedy, che applica il paradigmo divide-et-impera ed è caratterizzato da:
Si assume di lavorare con attributi con valori discreti (categoriali).
L'albero è costruito in modo ricorsivo.
All'inizio tutti gli esempi del training set sono messi nella radice.
Gli esempi sono partizionati in modo ricorsivo selezionato attributo dopo attributo.
L'attributo utilizzato per la partizione ad ogni step è l'attributo che massimizza l'information gain rispetto alla baseline.
Termino quando una partizione contiene tutte istanze della stessa classe; o quando non ci sono più attributi da utilizzare.
Una volta che termino associo alle istanze della partizione la classe più frequente.
L'algoritmo descritto è chiamato J48. Segue il relativo pseudo-codice

Notiamo come nello pseudo-codice dell'algoritmo è presente un parametro chiamato threshold, che mi permette di stabilire se non c'è nessun attributo che riesce ad ottenere dei risultati significativamente migliori rispetto alla baseline calcolata. Nel caso in cui il gain è sotto la soglia infatti, è inutile aumentare la complessità del modello.
Il principale svantaggio di questo tipo di modelli è che la loro complessità dipende dal numero di features.
3 Weka
Weka è un tool open source scritto in Java che mette a disposizione una collezione di algoritmi di apprendimento automatico.
3.1 Format ARFF
Weka utilizza il formato ARFF per processare i datasets. Esempio di
dataset ARFF: iris.arff .
Il dataset è il tipico iris dataset , menzionato nel classico
articolo di Fisher intitolato "The use of multiple measurements in
taxonomic problems".
Il formato ARFF per specificare il dataset iris inizia con le seguenti linee
@RELATION iris
@ATTRIBUTE sepallength REAL
@ATTRIBUTE sepalwidth REAL
@ATTRIBUTE petallength REAL
@ATTRIBUTE petalwidth REAL
@ATTRIBUTE class {Iris-setosa,Iris-versicolor,Iris-virginica}
successivamente poi troviamo i dati effettivi, in cui ogni riga corrisponde ad una istanza, e ogni istanza ha 5 colonne, di cui quattro sono valori reali e uno è il valore della classe. Notiamo che i dati sono di training, e quindi sono etichettati.
@DATA 5.1,3.5,1.4,0.2,Iris-setosa 4.9,3.0,1.4,0.2,Iris-setosa 4.7,3.2,1.3,0.2,Iris-setosa 4.6,3.1,1.5,0.2,Iris-setosa 5.0,3.6,1.4,0.2,Iris-setosa 5.4,3.9,1.7,0.4,Iris-setosa 4.6,3.4,1.4,0.3,Iris-setosa 5.0,3.4,1.5,0.2,Iris-setosa 4.4,2.9,1.4,0.2,Iris-setosa 4.9,3.1,1.5,0.1,Iris-setosa 5.4,3.7,1.5,0.2,Iris-setosa ... 6.5,3.0,5.2,2.0,Iris-virginica 6.2,3.4,5.4,2.3,Iris-virginica 5.9,3.0,5.1,1.8,Iris-virginica
3.2 Weka Interface
Per quanto riguarda il training, possiamo applicare quattro opzioni:
percentage-split: applica dello shuffle. In ogni caso comunque i risultati ottenuti potrebbero non essere robusti. La cross-validation ci permette di ottenere dei risultati più robusti.
use training set:
Supplied test set:
n-fold cross-validation: permette di avere \(n\) misure di \(n\) sottoinsiemi del dataset dato. Il modo in cui poi utilizzo queste n misure dipende da quello che voglio fare. Nel caso di WEKA la cross-validation viene effettuata solamente sul training.
Problema di question classification: capire che tipo di informazione voglio avere data una domanda.
3.3 Tree Visualization
Come abbiamo già detto, la proprietà più interessante dell'utilizzo degli alberi di decisioni è il fatto che una volta costurito l'albero è trasparente, nel senso che è possibile leggere le regole di inferenza apprese che veranno utilizzate per classificare i vari elementi.
Tramite weka poi siamo in grado di visualizzare tale albero.