WMR 13 - Hidden Markov Models I
Lecture Info
Date:
Course Site: Web Mining e Retrieval (a.a. 2019/20)
Lecturer: Roberto Basili.
Slides: ()
Table of Contents:
In questa lezione vediamo come poter trattare fenomeni sequenziali linguistici (ma non solo) attraverso un approccio Bayesiano tramite l'utilizzo di modelli markoviani noti cone il nome di Hidden Markov Models. Questi modelli vengono utilizzati per prendere decisioni in un contesto in cui abbiamo una sequenza di eventi certi di cui però non conosciamo le cause, ovvero non conosciamo gli stati interni che hanno generato quella sequenza.
1 Outline
In questa serie di lezioni rispetto agli hidden markov models affronteremo i seguenti argomenti:
Prima introduciamo il concetto di modello statistico per un linguaggio.
Poi introduciamo gli hidden markov models.
Infine impararemo un modo per apprendere un hidden markov model dai dati (Baun-Welch method), per poi generalizzarlo ad altri task.
2 Linguistic Structures
Come abbiamo visto nelle precedenti lezioni le strutture linguistiche sintattiche veicolano delle informazioni cruciali per il machine learning. Il modello più utilizzato per rappresentare queste strutture sintattiche sono le grammatiche formali.
S -> NP V S -> NP NP -> PN NP -> N NP -> Adj N N -> "imposta" V -> "imposta" Adj -> "pesane" PN -> "Pesante"
Utilizzando le grammatiche formali possiamo infatti lavorare con delle rappresentazioni alboree della sintassi della frase. Queste strutture vengono chiamate parse trees.
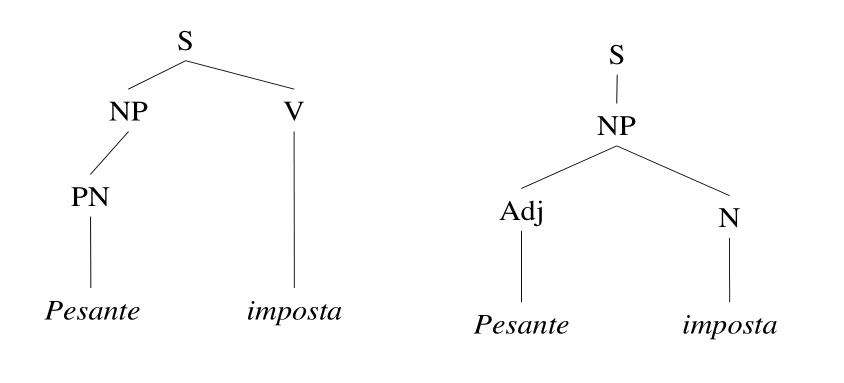
Notiamo che alcuni parse più sono più "rari" di altri, nel senso che raramente incontriamo strutture del genere nell'utilizzo comune della lingua. Nell'esempio precedente il parse tree a sinistra è molto strano, in quanto "Pesante" viene interpretato come il nome proprio di una persona, e "imposta" come un verbo diretto.
Per cercare di modellare questa differenza tra parse tree "rari" e parse tree "comuni" possiamo introdurre delle probabilità alle varie regole di una grammatica formale, ottenendo così facendo delle grammatiche formali probabilistiche. La probabilità associata ad una regola rappresenta la probabilità di utilizzare quella particolare regola di trasformazione durante la generazione della frase.
S -> NP V 0.7 S -> NP 0.3 NP -> PN 0.1 NP -> N 0.6 NP -> Adj N 0.3 N -> "imposta" 0.6 V -> "imposta" 0.4 Adj -> "pesane" 0.8 PN -> "Pesante" 0.2
L'introduzione della probabilità ci permette di associare ad ogni parse tree un valore di probabilità, ottenuto moltiplicando i valori di probabilità associati alla presenza di ogni regola (arco) che compone l'albero.
Rispetto all'esempio di prima troviamo le seguenti probabilità per i due parse trees:
\[\begin{split} P(((\text{Pesante})_{\text{Pn}} (\text{imposta})_{\text{V}})_{\text{S}}) &= 0.7 \cdot 0.1 \cdot 0.2 \cdot 0.4 = 0.0084 \\ \\ P(((\text{Pesante})_{\text{Adj}} (\text{imposta})_{\text{N}})_{\text{S}}) &= 0.3 \cdot 0.3 \cdot 0.8 \cdot 0.6 = 0.0432 \\ \end{split}\]
Introducendo le probabilità abbiamo i seguenti vantaggi:
Muovendoci verso gli alberi più probabili siamo quindi in grado di affrontare eventuali problematiche di ambiguità.
Potendo assegnare dei valori di probabilità anche ad alberi incompleti, o mal strutturati, siamo in grado di avere una maggiore tolleranza agli errori.
Passando dalla probabilità vado da un modello discreto in cui tutte le regole hanno la stessa importanza, ad un modello quantitativo che ci permette di utilizzare gli strumenti offerti dalla teoria della probabilità.
In questo momento pensiamo al linguaggio non come ad un teoria, ma come all'emergenza di eventi a cui possiamo assegnare delle probabilità (language in use).
3 Language Modelling
Supponiamo adesso di avere una sequenza di simboli che seguono una successione temporale rigida, ovvero totalmente ordinata rispetto al crescere del tempo, e che rappresentano dei segnali emessi da una certa sorgente.

Per modellare questo fenomeno possiamo utilizzare un language model, che assume che ogni emissione (simbolo) è una variabile aleatoria \(X\) tale che
Assume come valori i simboli presenti in un alfabeto \(A\).
Per descrivere l'incertezza del particolare segnale emesso si utilizza la probabilità
\[P(X = w_i) \;\;\;,\; w_i \in A\]
e quindi l'evento \((X_i = w_j)\) significa che all'i-esimo passo, ovvero all'i-esimo simbolo emesso, abbiamo incontrato la parola \(w_j\).
Dato che tutti i simboli emessi devono appartenere all'alfabeto \(A\), troviamo che
\[\sum_j P(X_i = w_j) = 1\]
3.1 N-Gram Models
Possiamo poi immaginare che in un certo istance di tempo la sorgente emittente si trovi in un certo stato, e quindi \(X_i\) rappresenta lo stato \(i\) esimo della sorgente. La generazione del segnale \(w_i\) dato lo stato attuale della sorgente \(X_i\) e la sua storia precedente può essere modellato con un modello bayesiano generativo che mette in relazione stato interno della sorgente e segnale emesso. Anche se possiamo sempre vedere i segnali emessi, non sempre saremmo in grado di analizzare gli stati interni.
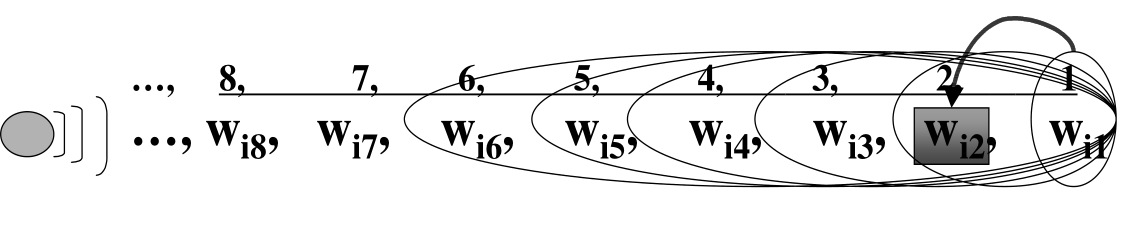
Formalmente esprimiamo questa idea tramite il seguente evento congiunto
\[\begin{split} P(&X_i = w_i, X_{i-1} = w_{i-1}, \ldots, X_1 = w_1) = \\ &= P(X_i = w_i | X_{i-1} = w_{i-1}, \ldots, X_1 = w_1) \cdot P(X_{i-1} = w_{i-1}, \ldots, X_1 = w_1) \end{split}\]
In altre parole stiamo dicendo che l'emmissione di nuove parole dipende dalle \(i-1\) parole precedenti. Chiameremo questo modello un i-gram. Generalmente invece si parla di n-gram language models quando abbiamo che le nuove parole dipendono dalle \(n-1\) precedenti.
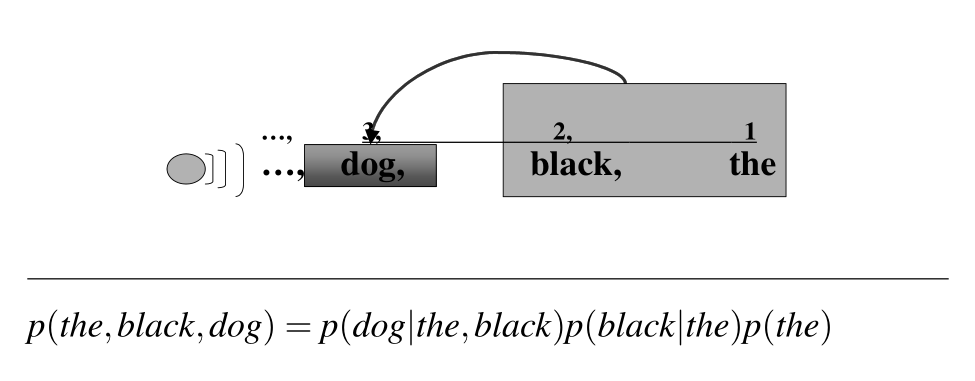
3.2 Stochastic Taggers/Grammars
Se poi considero al posto delle parole precedenti i precedenti Part-Of-Speech tags, allora ottenuto gli stochastic taggers

Se invece ricordo anche la struttura sintattica delle parole precedenti, allora ho delle stochastic grammars
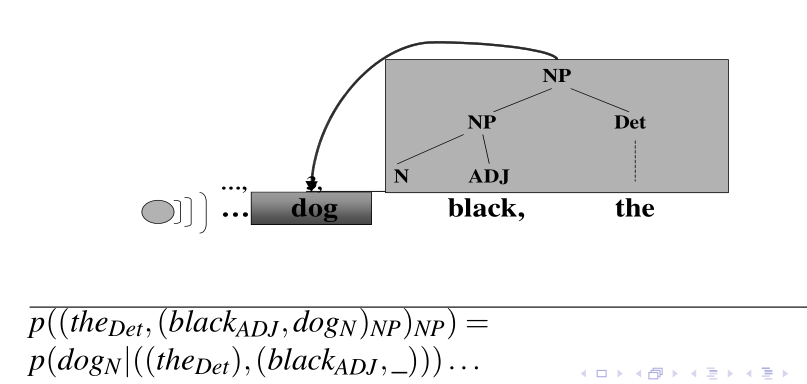
Observation: Un algoritmo di bin-search permette di esplorare in modo controllato uno spazio di istanze molto grandi andando salvare, ad ogni iterazione, solo le migliori \(k\) istanze trovate fino a quel momento.
3.3 Advantages
I vantaggi dell'utilizzo di modelli di linguaggio sono i seguenti
Faster Design.
Faster Processing.
Linguistic Adequacy
Acceptance.
Psychological Plausability.
Explanatory power.
4 Markov Model
Data una sequenza di variabili aleatorie \(X_1, X_2, \ldots, X_T\) ciascuna delle quali assume valori in un insieme numerabili \(W = \{p_1, p_2, \ldots, p_N\}\) detto anche state space, per avere una catena di Markov la sequenza di v.a. deve rispettare le seguenti due proprietà:
Limited horizon property: Si basa sul tagliare la dipendenza dell'osservazione futura dalla storia delle osservazioni passate.
\[P(X_{t+1} = p_k | X_1, ..., X_t) = P(X_{t+1} = p_k | X_t)\]
Time invariant: Al variare del tempo \(t\) le probabilità di passare da uno stato ad un altro non cambia
\[P(X_{t+1} = p_k | X_t = p_l) = P(X_2 = p_k | X_1 = p_l) \;\;\;\; \forall t > 1\]
Un modello di Markov può essere rappresentato analiticamente da una matrice di transizione \(A\), che contiene le varie probabilità di cambiamento tra stati. La matrice di transizione è definita come segue,
\[a_{i,j} = P(X_{t+1} = p_j \;\;|\;\; X_t = p_i)\]
notando poi che
\(\forall i, j \;\; a_{i,j} \geq 0\)
\(\forall i \;\; \sum_j a_{i, j} = 1\)
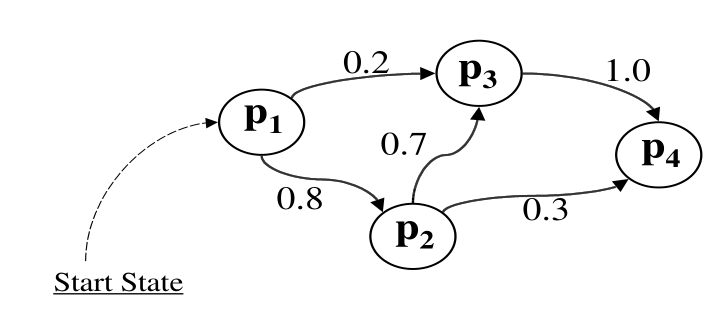
Graficamente possiamo rappresentare un modello di Markov con un grafo in cui i nodi sono i possibili stati in cui la catena si può trovare, e gli archi rappresentano le transizioni da stato in stato, e sono etichettati con le relative probabilità.
4.1 Visible Markov Model
Consideriamo una macchina del caffe "pazza", modellata come segue:
Abbiamo due stati: Tea Preferring (TP) e Coffee Prefering (CP).
In modo randomico la macchina cambia da uno stato ad un'altro.
Un markov model semplice (o visibile), quello in cui la macchina in modo deterministico ci dà il Te quando si trova nello stato TP e il caffe quando si trova nello stato CP. In questo caso l'unica aleatorità nella macchina è il suo switchare in modo aleatorio tra uno stato e l'altro. Per descrivere la macchina necessitiamo quindi di una descrizione del cambiamento randomico degli eventi. Formalmente, per ogni time step \(n\) e per ogni coppia di stati \(p_i\) e \(p_j\) dobbiamo determinare o stimare le seguenti probabilità
\[\begin{split} P(X_{n+1} = p_j | X_n = p_i) \\ P(X_{n+1} = p_i | X_n = p_j) \\ P(X_{n+1} = p_i | X_n = p_i) \\ P(X_{n+1} = p_j | X_n = p_j) \\ \end{split}\]
Un particolare esempio di queste probabilità è dato dal seguente grafo
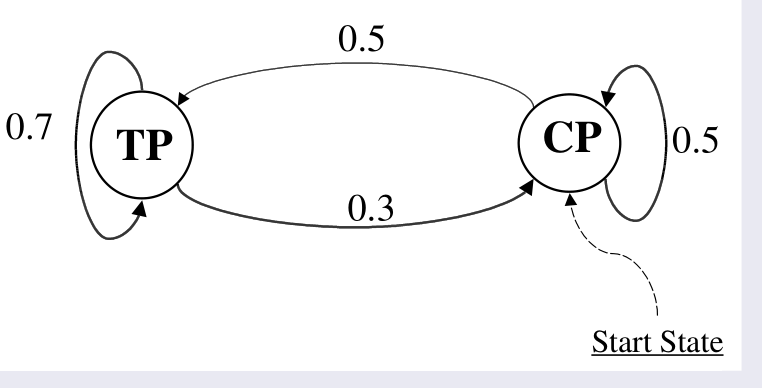
A questo punto possiamo rispondere alle seguenti domande:
Probabilità che al tempo \(3\) la macchina si trova nello stato TP.
\[P(X_3 = \text{TP}) = P(\text{(CP, CP, TP) and (CP, TP, TP)} = \ldots = 0.60\]
Probabilità che al tempo \(n\) la macchina si trova nello stato TP.
Probabilità della seguente sequenza di output (Coffee, Tea, Coffee).
\[\begin{split} P(\text{Cof, Tea, Cof}) &= P(\text{Cof}) \cdot P(\text{Tea | Cof}) \cdot P(\text{Cof | Tea}) \\ &= 1 \cdot 0.5 \cdot 0.3 = 0.15 \\ \end{split}\]
4.2 Hidden Markov Model
Molti dei problemi decisionali si basano sull'utilizzo di osservazioni "parziali", ovvero di osservazioni in cui si vede il comportamento/l'output del sistema ma non si vede la causa (lo stato interno) che ha portato il sistema a generare quel particolare output.
Consideriamo la macchina del caffe dell'esempio precedente. Se cambiamo la macchina e la rendiamo tale che non c'è una associazione deterministica tra stato (coffe preferring o te preferring) e evento (se ci da il caffe o o il te), otteniamo una Hidden Markov Model, in cui ciò che non riesco a vedere (lo stato), cambia in modo stocastico e determina la distribuzione dei possibili output.
Per descrivere la nuova macchina necessitiamo di definire per ogni time step \(n\) e per ogni output \(O = \{\text{Tea}, \text{Cof}, \text{Cap}\}\) le seguenti probabilità
\[P(O_n = k | X_n = p_i, X_{n+1} = p_j)\]
dove \(k\) è uno tra i valori in \(O\). La matrice che contiene queste probabilità condizionate è detta output matrix della macchina, o il suo hidden markov model.
Ad esempio, possiamo avere la seguente matrice
\[\begin{array}{c | c | c | c} \text{} & \textbf{Tea} & \textbf{Coffee} & \textbf{Capuccino} \\ \hline \textbf{TP} & 0.8 & 0.2 & 0.0 \\ \textbf{CP} & 0.15 & 0.65 & 0.2 \\ \end{array}\]
La matrice deve essere letta nel seguente modo: quando esco da \(\text{TP}\) emetto con \(80\%\) di probabilità un te e con il \(20\%\) di probabilità un caffe, mentre quando esco da \(\text{CP}\) emetto con \(15\%\) di probabilità un te, con il \(65\%\) di probabilità un caffe e con \(20\%\) di probabilità un cappuccino.
Supponendo poi che la macchina parte dallo stato \(\text{CP}\) possiamo rispondere alle seguenti domande
La probabilità di avere la sequenza di output \(\text{(Cappuccino, Coffee)}\) data la sequenza di stati interni \(\text{CP, TP, TP}\).
\[P(O_1 = \text{Cap}, O_2 = \text{Cof}, X_1 = \text{CP}, X_2 = \text{TP}, X_3 = \text{TP}) = \ldots = 0.04\]
La probabilità di output \(\text{(Tea, Coffee)}\) per ogni state sequence.
Un generico output \(O = \{o_1, \ldots, o_n\}\) per ogni state sequence.
Notiamo come l'ultimo problema ci richiede di calcolare la likelihood. In particolare, possiamo stimare la probabilità di vedere gli \(n\) simboli \(O = (o_1, \ldots, o_n)\) fuori da una sequenza di \(n+1\) transizioni \(X = (p_1, \ldots, p_{n+1})\) tramite la seguente probabilità
\[\begin{split} P(O) &= \sum\limits_{p_1, \ldots, p_{n+1}} P(O|X) \cdot P(X) \\ &= \sum\limits_{p_1, \ldots, p_{n+1}} P(p_1) \prod\limits_{t = 1}^n P(O_t | p_t, p_{t+1}) P(p_{t+1}|p_t) \\ \end{split}\]
Per modellare un linguaggio possiamo lavorare sulle probabilità condizionali \(P(O_t | p_t, p_{t+1})\) andando quindi ad eliminare la probabilità di emettere un dato segnale rispetto ad una data transizione di stati. Possiamo poi vincolare le possibili sequenze di stati interni.
4.2.1 Problems solved by HMM
In generale i tre problemi fondamentali che il modello delle HMM vuole risolvere sono:
Language Modeling (computing likelihood): Data unba sequenza di osservazioni \(O = O_1, \ldots, O_n\) e un modello \(\lambda = (E, T, \pi)\), come calcolo la probabiità di generare tale sequenza da tale modello \(P(O|\lambda)\)? (Risolto da forward chaining)
Tagging/Decoding: Data unba sequenza di osservazioni \(O = O_1, \ldots, O_n\) e un modello \(\lambda = (E, T, \pi)\), come possiamo trovare l'ottima sequenza di stati interni \(Q = q_1, \ldots, q_n\) che mi hanno portato a generare la sequenza visibile \(O\)? (Risolto da Viterbi algorithm)
Model Induction: Come stimo i parametri del modello \(\lambda = (E, T, \pi)\) in modo tale da massimizzare \(P(O|\lambda)\)? (Risolto da Expectation maximization)
5 PoS Tagging
Consideriamo il problema del Part-Of-Speech tagging, che consiste, data una sequenza di morfemi \(w_1, \ldots, w_n\) con delle descrizioni sintattiche ambigue (part-of-speech tags), di assegnare la sequenza degli n POS tags \(t_{j_1}, \ldots, t_{j_n}\) che caratterizzano tutte le parole \(w_i\).
Ad esempio, "Secretariat is expected to race tomorrow". Possiamo assegnare a questa frase le seguenti sequence di POS tags
NNP VBZ VBN TO VB NR NNP VBZ VBN TO NN NR
Per capire quale sequenza tra le due date è la più promettente possiamo utilizzare un modello markoviano rappresentato dal seguente grafo

notiamo che i nodi del grafo, che rappresentano gli stati della catena, sono le part of speech.
Data una sequenza di morfemi \(w_1, \ldots, w_n\) vogliamo trovare i POS tags che massimizzano la probabilità
\[P(w_1, \ldots, w_n, t_1, \ldots, t_n)\]
ovvero tali che
\[(t_1, \ldots, t_n) =\underset{\text{pos}_1, \ldots, \text{pos}_n}{\text{argmax}} P(w_1, \ldots, w_n, \text{pos}_1, \ldots, \text{pos}_n)\]
Dato poi che siamo interessati solamente all'argmax, possiamo utilizzare il fatto che
\[P(w_1, \ldots, w_n, \text{pos}_1, \ldots, \text{pos}_n) = P(\text{pos}_1, \ldots, \text{pos}_n | w_1, \ldots, w_n) \cdot P(w_1, \ldots, w_n)\]
e dal fatto che \(P(w_1, \ldots, w_n)\) è costante al variare dei pos tags, per considerare solamente i tags che massimizzano la seguente probabilità
\[(t_1, \ldots, t_n) =\underset{\text{pos}_1, \ldots, \text{pos}_n}{\text{argmax}} P(\text{pos}_1, \ldots, \text{pos}_n | w_1, \ldots, w_n)\]
Utilizzando poi la legge di Bayes troviamo
\[(t_1, \ldots, t_n) =\underset{\text{pos}_1, \ldots, \text{pos}_n}{\text{argmax}} P(w_1, \ldots, w_n | \text{pos}_1, \ldots, \text{pos}_n) \cdot P(\text{pos}_1, \ldots, \text{pos}_n)\]