WMR 14 - Hidden Markov Models II
Lecture Info
Date:
Course Site: Web Mining e Retrieval (a.a. 2019/20)
Lecturer: Roberto Basili.
Slides: ()
Table of Contents:
In questa lezione abbiamo ripreso da dove l'avevamo lasciato il problema di risolvere il POS tagging tramite un HMM. In questa lezione in particolare abbiamo visto il forward algorithm, il viterbi algorithm, e il metodo Baum-Welch
1 HMM for Pos Tagging
Ad ogni parola possiamo associare uno o più part of speech. Il problema della decodifica è quindi quello di capire i POS delle parole a partire dalla frase.
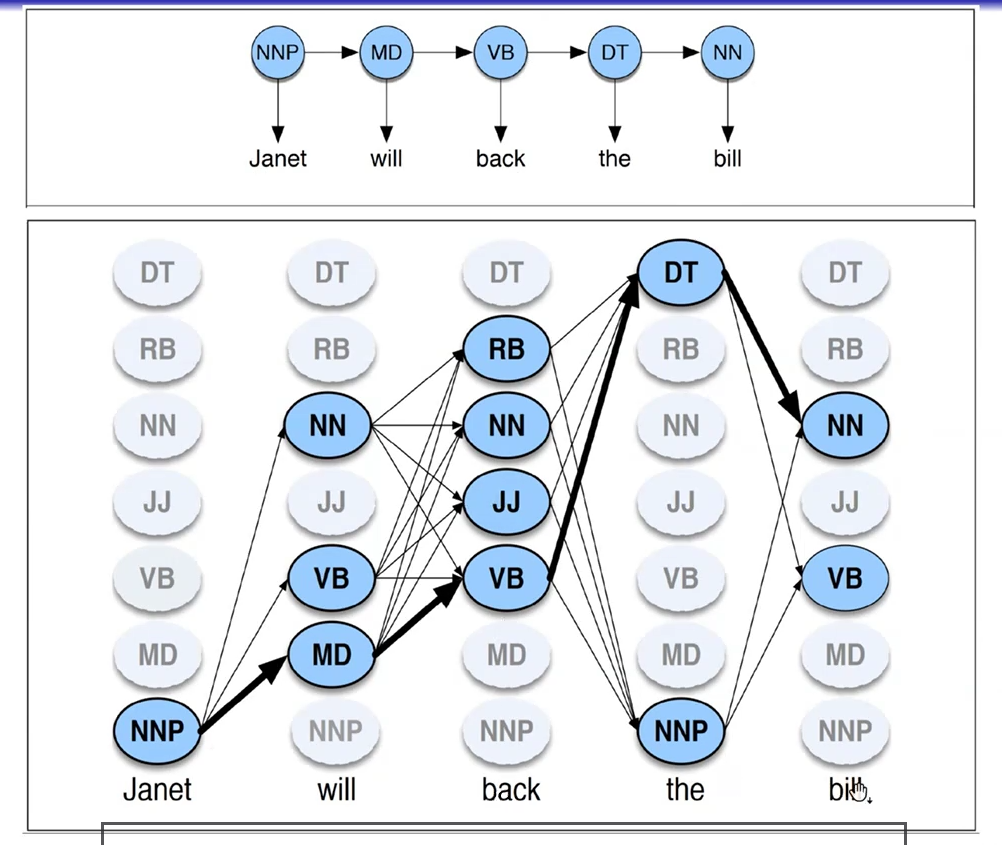
Tramite una modellazione HMM possiamo estrarre la sequenza dei pos tags che massimizza la likelihood. Così facendo siamo in grado di eliminare l'ambiguità.
La struttura dati che contiene tutti i possibili pos tags per ogni parola e le possibili transizioni da pos tag a pos tag è chiamata trellis.
Nell'ultima lezione avevamo poi modellato il problema del pos tagging come trovare i valori dei tags \(t_1, \ldots, t_n\) tali che
\[(t_1, \ldots, t_n) =\underset{\text{pos}_1, \ldots, \text{pos}_n}{\text{argmax}} P(w_1, \ldots, w_n | \text{pos}_1, \ldots, \text{pos}_n) \cdot P(\text{pos}_1, \ldots, \text{pos}_n)\]
1.1 Questions in POS tagging
Andando a rivedere i tre problemi fondamentali risolti dalle HMM ma in un contesto di POS tagging notiamo le seguenti cose:
Il primo problema, ovvero quello di calcolare la likelihood, non è molto interessante, in quanto non abbiamo molto interesse a sapere qual è la probabilità di generare la sequenza delle parole \((w_1, \ldots, w_n)\).
Il problema del decoding invece è fondamentale, in quanto essenzialmente è proprio ciò che il POS tagging ci richiede di fare. Questo problema può essere risolto dall'algoritmo di Viterbi, un algoritmo di programmazione dinamica.
Per il terzo problema invece utilizzeremo l'algoritmo di Baum-Welch, che è un particolare caso dell'algoritmo più generale di Expectation-Maximization.
1.2 Advantages of using HMM
Alcuni vantaggi nell'utilizzo di HMM per il POS tagging:
Basati sulla teoria della probabilità (sound theory).
L'algoritmo di inferenza (l'algoritmo di Viterbi) è lineare rispetto alla lunghezza della sequenza.
Metodi sound per confrontare modelli e stime diverse.
2 Forward Algorithm
Il forward algorithm utilizza il trellis in una sola direzione: in avanti, ovvero guarda dalla prima parola all'n-esima. Un esempio di esecuzione dell'algoritmo è riportato a seguire
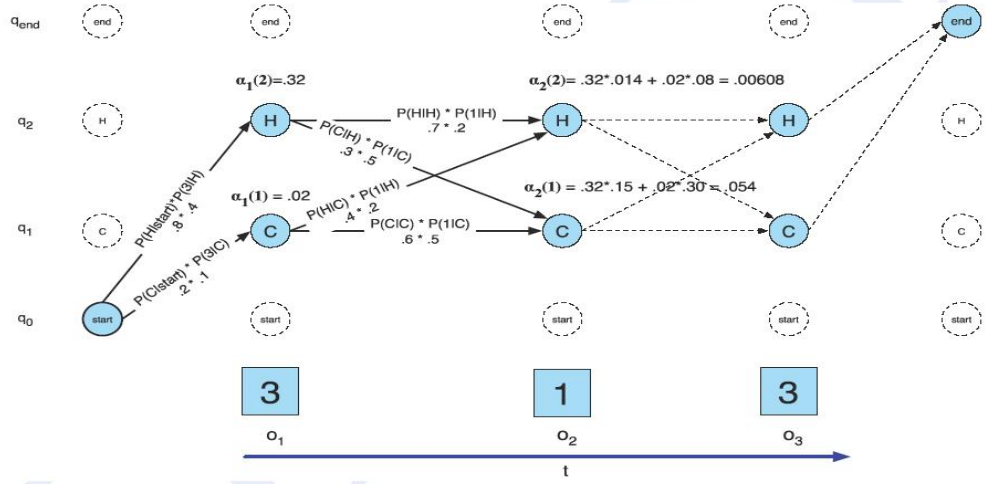
Tra tutti gli stati possibili della nostra HMM ne aggiungiamo due di fitizzi: quello iniziale, \(q_0\), e quello finale, \(q_{\text{end}}\). Si prendono poi in considerazione le transizioni che partono dallo stato \(q_0\) e arrivano ai due stati interni possibili, che sono \(H\) e \(C\) (possiamo considerarli come testa e croce).
Ad ogni tempo \(t\) il forward algorithm ci produce la probabilità complessiva associata alla stringa letta fino al tempo \(t\). In particolare definiamo \(\alpha_t(j)\) come la seguente probabilità
\[\alpha_t(j) = P(o_1, o_2, \ldots, o_t, q_t = j | \lambda)\]
La computazione necessaria per calcolare tale probabilità è ottenuta andando a memorizzare per ciascun nodo della matrice vista in figura la probabilità complessiva di tutti i cammini che terminano in quel nodo a partire dai simboli osservati (da sinistra verso destra). Formalmente,
\[\alpha_t(j) = \sum\limits_{i = 1}^{N-1} \alpha_{t-1}(i) \cdot a_{i,j} \cdot b_j(o_t)\]
dove,
\(a_{i, j}\) indica la probabilità di effettuare una transizione dallo stato interno \(q_i\) allo stato interno \(q_j\);
\(b_j(o_t)\) indica la probabilità di emettere il simbolo \(o_t\) a partire dallo stato interno \(q_j\) al tempo \(t\).
Ad esempio,
\(\alpha_1(2)\) è il risultato di una transizione iniziale che entra in \(H\) e dell'emissione iniziale che da \(H\) genera il simbolo \(3\). La probabilità per passare da start ad \(H\) è nota ed è pari a \(P(H|\text{start}) = 0.8\), mentre quella di generare \(3\) da \(H\) è nota ed è \(P(3 | H) = 0.4\).
\(\alpha_2(2)\) rappresenta invece la probabilità complessiva di trovarmi nello stato 2 (\(H\) nel nostro esempio), al tempo \(t=2\), dopo aver visto i primi due caratteri della stringa, che in questo caso sono \(3\;\;1\). Dato che ho due cammini per arrivare in tale stato al tempo \(t=2\), calcolo tale probabilità nel seguente modo
\[\begin{split} \alpha_2(2) &= P(H|H) \cdot P(1|H) + P(H|C) \cdot P(1|H) \\ &= .32 \cdot .14 + 0.2 \cdot 0.8 \\ &= 0.00608 \\ \end{split}\]
Osservazione: il forward algorithm non sta prendendo posizione sulla grammatica, ma calcola solo la probabilità che le varie sequenze di PoS-tagging hanno rispetto alla frase vista. In particolare quindi non possiamo utilizzare il forward algorithm per andare ad effettuare disambiguation.
2.1 Formal Description
Il forward algorithm può essere descritto nel seguente modo

Tale algoritmo può essere visto come operante in tre fasi distinte, che sono:
Nella prima fase si inizializzano i primi valori di \(\alpha_1(j)\) al variare di \(j\) come segue
\[\alpha_1(j) = a_{0, j} \cdot b_j(o_1) \;\;\;,\;\; 1 \leq j \leq N\]
dove \(a_{0, j} = \pi_j\), ovvero è la probabilità che la HMM inizialmente si trova nello stato \(q_j\).
Poi c'è una fase di ricorsione in cui si calcolano i successivi \(\alpha_t(j)\) a partire dai precedenti
\[\alpha_t(j) = \sum\limits_{i = 1}^{N-1} \alpha_{t-1}(i) \cdot a_{i, j} \cdot b_j(o_t) \;\;\;,\;\; 1 < j < N, \;\; 1 < t < T\]
Infine, c'è una fase di terminazione
\[P(O | \lambda) = \alpha(N) = \sum\limits_{i = 2}^{N-1} \alpha_T(i) \cdot a_{i, N}\]
3 Viterbi Algorithm
L'algoritmo forward appena visto non ci permette di risolvere il problema del decoding, in quanto nel decoding vogliamo capire qual è la sequenza dei pos tags che massimiza la probabilità di vedere quella particolare sequenza. Detto altrimenti, il Viterbi algorithm non è interessato alla probabilità totale della stringa, che viene calcolata dal forward algorithm, ma è interessato alla probabilità della migliore sequenza di POS tagging. In altre parole possiamo utilizzare l'algoritmo di Viterbi per disambiguare le sequenze di POS tagging.
In termine di approccio algoritmo, il Viterbi algorithm utilizza lo stesso approccio dinamico del forward algorithm, con la differenza però che ad ogni elemento del trellis è associato un viterbi score \(v_j(t)\), che esprime la seguente probabilità
\[P(q_0, q_1, \ldots, q_{t-1}, o_1, o_2, \ldots, o_t, q_t = j | \lambda)\]
ed è calcolato come segue
\[v_t(j) = \underset{1 \leq i \leq N-1}{\max} v_{t-1}(i) \cdot a_{i,j} \cdot b_j(o_t)\]
In altre parole, ad ogni passo massimizzo la provenienza, e quindi considero solamente il cammino che mi permette di arrivare in quello stato andando a massimizzare la probabilità.
Per fare questo l'algoritmo utilizza un backpointer per ogni nodo considerato. Il backpointer infatti rappresenta il particolare nodo del livello precedente che mi ha permesso di massimizzare la probabilità dei tags. Alla fine i backpointer vengono utilizzati per ricostruire la sequenza dei pos tags desiderata.
3.1 Formal Description
L'algoritmo di viterbi è così descritto

4 Parameter Estimation
Notiamo che sia il Viterbi algorithm sia il Forward algorithm fanno utilizzo delle probabilità di transizione \(\alpha_{i, j}\) e delle probabilità di emissione \(b_j(o_t)\). Andiamo adesso a vedere dei metodi che ci permettono di stimare queste probabilità.
4.1 Supervised Methods
Se lavoro con un dataset etichettato, ovvero nei metodi supervisionati, trovo la seguente situazione:
Probabilità di emissione, possiamo stimarla tramite la seguente frequenza
\[P(w_i | q_j) = \frac{C(w_i, q_j)}{C(q_j)}\]
questo ci sta dicendo che per capire la probabilità di emettere la parola \(w_i\) a partire dallo stato \(q_j\) devo calcolare quante volte emetto \(w_i\) a partire da \(q_j\) e dividere tale numero rispetto al numero totale di emissioni a partire da \(q_j\). Dato che molto spesso i dati a disposizione sono pochi, è poi possibile effettuare lo smoothing di Laplace (Manning & Schutze, Chapter 6), per ottenere
\[P(w_i | q_j) = \frac{C(w_i, q_j) + 1}{C(q_j) + K_i}\]
dove \(K_i\) è il size del dizionario di possibili part of speech associati alla parola \(w_i\).
Probabilità di transizione: Le probabilità di transizioni invece sono stimate nello stesso modo con un semplice calcolo di frequenza
\[P(q_i | q_j) = \frac{P(q_i \text{ follows } q_j)}{C(q_j)}\]
Anche in questo caso è possiible effettuare dello smoothing. Detto questo, tipicamente è meno necessario, in quanto il numero limitate dei pos tags fa sì che ci siano molti esempi di ogni possibile transizione da pos tag a pos tag.
4.2 Unsupervised Methods
Se invece dobbiamo stimare tramite dei metodi semi-supervised o unsupervised, ovvero quando abbiamo pochi dati annotati a disposizione possiamo utilizzare vari metodi.
Ad esempio possiamo stimare da un dizionario \(D\) le probabilità di emissione iniziali \(P(w_i, q_j)\), mentre assegno in modo casuale le probabilità di transizione \(P(q_i | q_j)\).
Oppure posso avere una situazione di \(u_L\) learning (Kupiec, 92), in cui ho molti dati non etichettati e ho un piccolo insieme di dati etichettati. L'idea è quella di creare degli stimatori probabilistici basati su delle classi di equivalenza formate da più etichette grammaticali.
\[P(w_i | p_L) = \frac{\frac{1}{|L|} c(u_L)}{\sum_{u^{L^{'}}} \frac{C(u^{L^{'}})}{|L^{'}|}}\]
4.3 Baum-Welch Method
Il metodo di Baum-Welch è un algoritmo per apprendere i parametri del mio HMM e può essere utilizzato in un caso di unsupervised learning, ovvero quando non abbiamo dati etichettati. Questo metodo è un caso particolare dell'algoritmo di Expectation Maximization, e ci permette di dar conto delle tendenze statistiche del modello sfruttando la distribuzione dei casi nel corpus.
Dato un modello HMM \(\lambda = (E, T, \pi)\), in cui \(E\) è la matrice delle emissioni, \(T\) è la matrice delle transizioni e \(\pi\) è il vettore delle probabilità iniziali, e una storia di osservazioni \(Z = (z_1, z_2, \ldots, z_t)\) applicando il metodo Baum-Welch siamo in grado di trasformare il modello \(\lambda\) in un nuovo modello HMM \(\lambda^{'}\) in modo tale da spiegare le osservazioni \(Z\) in modo migliore, ovvero tale che
\[P(Z | \lambda^{'}) \geq P(Z | \lambda)\]
Anche se idealmente vorremo trovare il modello che massimizza la probabilità \(P(Z | \lambda)\), questo in pratica è un problema non risolvibile in tempi decenti. Siamo dunque interessati ad un algoritmo che converge ad un massimo locale, e non a quello globale.
In generale per avere un learning efficiente necessitiamo un sacco di dati, ovvero delle storie di osservazioni molto lunghe.
4.3.1 Forward-Backward Algorithm
Questo metodo è noto anche con il nome di forward-backward algorithm, ed è così descritto:
Parto con una stima iniziale delle varie probabilità.
Applico il modello \(\lambda\) alle osservazioni e calcolo l'expectation di quante volte ciascuna transazione e ciascuna emissione viene utilizzata per generare la storia delle osservazioni.
Effettuo una re-estimation delle probabilità basandomi sulle expectations calcolato al passo precedente.
Questo procedimento viene ripetuto fino ad ottenere una convergenza.
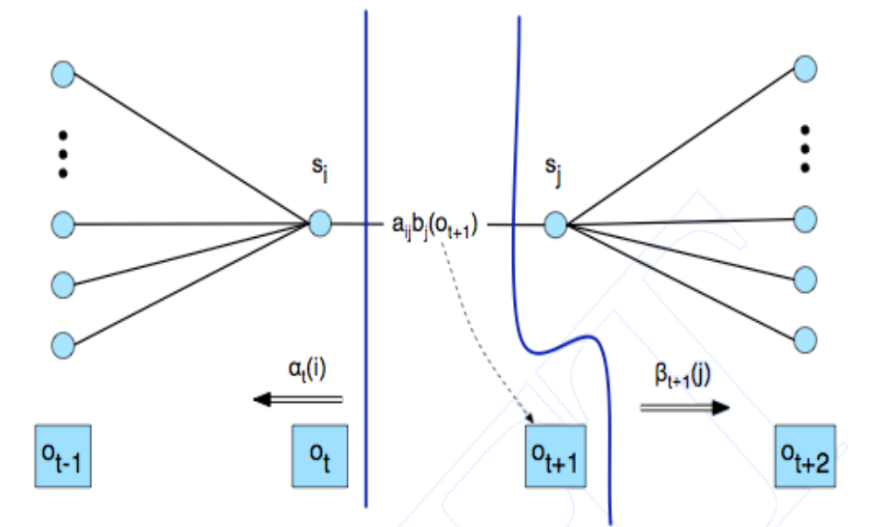
Le forward probabilities, indicate con \(\alpha_t(i)\) ci dicono la probabilità di arrivare dall'inizio della frase fino al punto \(s_i\). Formalmente,
\[\alpha_k(s) = P(o_1, \ldots, o_k | x_k = s, \lambda)\]
e sono calcolate ricorsivamente come segue
\[\alpha_{k+1}(q) = \sum\limits_{s \in S} \alpha_k(s) \cdot a_{s, q} \cdot b_q (o_{k+1})\]
con \(\alpha_1(q) = \pi_q)\) come caso base.
Le backward probabilities \(\beta_{t+1}(j)\) invece ci dicono la probabilità di partire dallo stato \(s_j\) e ottenere esattamente la frase a partire da \(o_{t+2}\) fino alla fine della frase. Formalmente,
\[\beta_k(s) = P(o_k, \ldots, o_t | x_k = s, \lambda)\]
e sono calcolate ricorsivamente come segue
\[\beta_k(s) = \sum\limits_{q \in S} a_{s, q} \cdot b_q(o_{k+1}) \cdot \beta_{k+1}(q)\]
A partire da queste probabilità posso poi calcolare il numero di volte in cui passo per un certo stato in un certo stato \(s\). Formalmente,
\[\gamma_k(s) = P(X_k = s | Z, \lambda)\]
Trovo infatti
\[\gamma(s) = \frac{\alpha_k(s) \cdot \beta_k(s)}{P(X_k | Z, \lambda)} = \frac{\alpha_k(s) \cdot \beta_k(s)}{\sum_{q \in S} \alpha_k(q)}\]
A questo punto posso considerare il numero medio in cui effettuo delle transizioni a partire dallo stato \(s\).
\[\mathbb{E}[\text{# of transitions from } s] = \sum\limits_{k = 1}^{t-1} \gamma_k(s)\]
Nello stesso modo, posso definire la probabilità di stare nello stato \(q\) al tempo \(k\) e nello stato \(s\) al tempo \(k+1\), ovvero la probabilità di effettuare una transizione da \(q\) ad \(s\) date le osservazioni e il modello corrente della HMM.
\[\xi_k(q, s) = P(X_k = q, X_{k+1} = s | Z, \lambda)\]
Tale valore può essere calcolato nel seguente modo
\[\xi_k(q, s) = \eta_k \cdot \alpha_k(q) \cdot T_{q, s} \cdot E_{s, o_{k+1}} \cdot \beta_{k+1}(s)\]
dove \(\eta_k\) è un fattore di normalizzazione tale che
\[\sum\limits_{q, s} \xi_k(q, s) = 1\]
Infine, posso considerare il numero atteso di volte in cui ho una transizione che mi porta lo stato da \(q\) a \(s\).
\[\mathbb{E}[\text{# of transitions from q to s}] = \sum\limits_{k = 1}^{t-1} \xi_k(q, s)\]
Una volta che abbiamo calcolato tutte queste quantità possiamo costruire il nuovo modello \(\hat{\lambda} = (\hat{E}, \hat{T}, \hat{\pi})\). Notiamo in ogni caso che i due modelli \(\hat{\lambda}\) e \(\lambda\) condividono sia l'insieme degli stati che l'insieme delle osservazioni.
Il modello è costruito come segue.
Condizioni iniziali: Le nuove condizioni iniziali sono ottenute tramite dello smoothing
\[\hat{\pi}_s = \gamma_1(s)\]
Matrice di transizione: Le nuove entry della matrice di transizione sono calcolate come segue
\[\hat{T}_{q, s} = \frac{\mathbb{E}[\text{# of transitions from q to s}]}{\mathbb{E}[\text{# of transitions from q}]} = \frac{\sum\limits_{k = 1}^{t-1} \xi_k(q, s)}{\sum\limits_{k = 1}^{t-1} \gamma_k(q)}\]
Matrice di emissione: Le nuove entry della matrice di emissione sono calcolate come segue
\[\begin{split} \hat{E}_{s, 0} = \hat{b}_s(o) &= \frac{\mathbb{E}[\text{# of times in state s,observation was o}]}{\mathbb{E}[\text{# of times in state s}]} \\ &= \frac{\sum_{k = 1}^t \gamma_k(s) \cdot \mathbf{1}(z_k = 0)}{\sum_{k = 1}^t \gamma_k(s)} \end{split}\]
4.3.2 Expectation Step (E-step)
Lo step di expectation è quello in cui si calcolano le seguenti quantità
\[\begin{split} \sum_{k = 1}^t \gamma_k(i) &= \text{expected number of transitions involving } q_i \\ \\ \sum_{k = 1}^{t-1} \xi(i, j) &= \text{expected number of transitions from } q_i \text{ to } q_j\\ \end{split}\]
4.3.3 Maximization Step (M-step)
mentre il maximization step è quello in cui facciamo la re-estimation dei vari parametri del modello
\[\begin{split} \hat{a}_{i, j} &= \frac{\sum_{k = 1}^{t-1} \xi_k(i, j) }{\sum_{k = 1}^{t-1} \gamma_k(j)} \\ \\ \hat{b}_i(s) &= \frac{\sum_{k = 1}^{t-1} \gamma_k(i) \cdot \mathbf{1}(o_k = s)}{\sum_{k = 1}^{t-1} \gamma_k(j)} \end{split}\]
4.3.4 Example of Baum-Welch
5 References
TODO.
6 Exercise
TODO.