WMR 15 - Hidden Markov Models III
Lecture Info
Date:
Course Site: Web Mining e Retrieval (a.a. 2019/20)
Lecturer: Roberto Basili.
Slides: ()
Table of Contents:
In questa lezione chiudiamo la parte relative alle HMM.
1 Review
1.1 Types of HMM problems
L'ultima volta avevamo analizzato i tre problemi affrontabili utilizzando un modello di Hidden Markov Models, che per ricapitolare sono:
Statistical Language Modelling: Consiste nel calcolare la probabilità della generazione di una particolare frase tramite un modello di linguaggio. Questo problema è risolto da riconoscitori vocali come alexa, che devono capire come i suoni sono concatenati e tagliati in unità lessicali, e come la sequenza lessicale ha una sua dignità linguistica. Avendo tante sequenze possibili, il language modelling permette di avere un criterio probabilistico per ordinare le varie sequenze tra loro in base al loro valore di probabilità.
Decoding: Problema di traduzione in cui si riconducono i simboli osservabili agli stati nascosti del modello. Questo problema è risolto dall'algoritmo di Viterbi, che ci permette di annotare velocemente i simboli osservabili con gli stati nascosti. L'algoritmo di Viterbi, utilizzando il trellis, associa in tempo lineare ad ogni ticktime la probabilità migliore fino a quel punto relativa alle transizioni di stato e alle emissioni di ciò che abbiamo già osservato.
Model Induction: Questo problema consiste nel trovare un metodo per migliorare il modello con cui sto lavorando. Risolvere questo problema significa essere in grado di apprendere il modello dai dati.
1.2 Viterbi Algorithm
Notiamo che nella massimizzazione della probabilità per arrivare allo stato \(t\) partendo dallo stato \(s\) eseguiamo il seguente calcolo
\[\text{viterbi}[s, t] \gets \underset{\ \leq s^{'} \leq \text{num-states}}{\max} \text{viterbi}[s^{'}, t- 1] \cdot a_{s^{'}, s} \cdot b_s(o_t)\]
dato che il termine \(b_s(o_t)\) non dipende da \(s^{'}\), abbiamo che tale termine è superfluo per il calcolo del massimo, e quindi nel calcolo del backpointer possiamo risparmiare una moltiplicazione e non considerarlo.
2 Baum-Welch Method
Andiamo adesso a vedere come migliorare la stima delle matrici data una HMM.
Iniziamo ricordando che apprendere un modello HMM significa apprendere tutti i parametri del modello. Dato che lavoriamo con una HMM, il modello può essere espresso come una tripla \(\lambda = (E, T, \pi)\), dove
\(E\) è la matrice che contiene le probabilità di transizioni.
\(T\) è la matrice delle emissioni.
\(\pi\) vettore delle probabilità iniziali.
In generale è difficile avere dei dati etichettati con cui effettuare il nostro training set. Inoltre, in questo caso particolare vogliamo dei dati etichettati in una particolare sequenza, il che rende il tutto ancora più difficile, in quanto ci servono ancora più dati.
Per cercare di utilizzare al meglio i pochi dati etichettati che si hanno a disposizione si utilizzano quindi delle metodologie statistiche. Questo può essere fatto in vari modi. Uno di questi è quello di utilizzare la grande quantità di dati osservati di cui però il sistema non ha il corretto decoding.
Quello che cerchiamo in particolare è un algoritmo in grado di fare decoding, ma che comunque si comporta bene rispetto all'assegnazione di probabilità alle varie sequenze di simboli. Per fare questo possiamo pensare di partire da un modello base \(\lambda\) e da una serie di osservazioni \(Z = (z_1, z_2, \ldots, z_t)\), e di costruire una sequenza di modelli \(\lambda_1, \lambda_2, \ldots, \lambda_k\) in modo tale che ciascun modello si comporta sicuramente in modo non-peggiore rispetto al precedente. Questo procedimento di migliorazione può essere ripetuto fino a quando raggiungiamo un punto fisso, ovvero quando raggiungiamo un modello che ci offre un massimo locale rispetto alle performance.
2.1 Overall Scheme
Baum-Welch è il metodo matematico di natura statistico che ci permette di costruire la successione dei modelli precedentemente menzionata. Il metodo si basa sull'algoritmo generale della expectation maximization.
Tale metodo si basa sul seguente schema:
Start with initial probability estimates;
Compute expectations of how often each transition/emission is used;
Re-estimate the probabilities based on those expectations.
Questi steps sono ripetuti fino a quando si arriva ad una situazione di convergenza.
2.2 Forward/Backward Probabilities
L'idea alla base di questo modello è di analizzare i fenomeni che avvengono in media nella successione \(Z\) che si ha a disposizione, per migliorare il modello.
Piuttosto che contare delle medie frequentiste, che necessiterebbero di aver fissato una particolare situazione, l'idea è quella di calcolare le probabilità utilizzando il modello di partenza \(\lambda_i\), fare la media delle probabilità, e assegnare questa media come la nuova probabilità del nuovo modello \(\lambda_{i+1}\).
Consideriamo il comportamento del modello \(\lambda\) al ticktime generico \(t\)
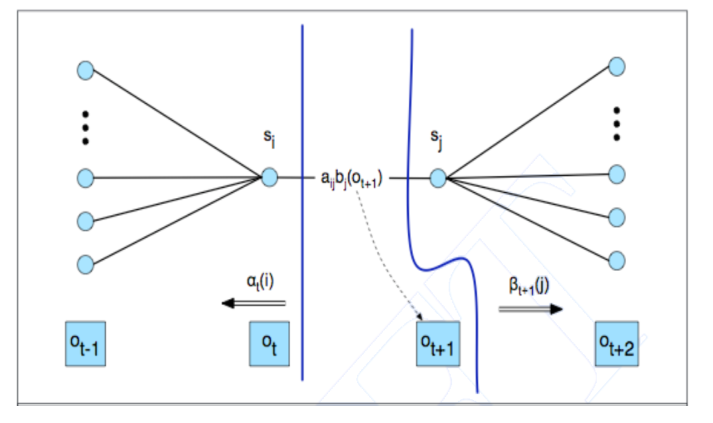
La probabilità che mi muovo da \(s_i\) a \(s_j\) è data dalla forward probability \(\alpha(i)\), che racchiude la probabilità di trovarmi nello stato \(s_i\) avendo visto la sequenzza \(o_{1}, \ldots, o_{t}\), dalla probabilità di transizionare da \(s_i\) a \(_j\), che è \(a_{i, j}\), dalla probabilità di emettere il simbolo \(o_{t+1}\) nello stato \(_j\), che è data da \(b_j(o_{t+1})\), e infine dalla backward probability \(\beta_{t+1}(j)\), che indica la probabilità di chiudere la storia delle osservazioni partendo al tempo \(t+1\) nello stato \(s_j\).
Per quanto riguarda le forward probabilities, ho la seguente definizione
\[\alpha_k(s) = P(o_1, \ldots, o_k, x_k = s | \lambda)\]
e sono calcolate ricorsivamente nel seguente modo
\[\begin{split} \alpha_1(q) &:= \pi_q \\ \alpha_{k+1}(q) &:= \sum\limits_{s \in S} \alpha_k(s) \cdot a_{s, q} \cdot b_q(o_{k+1}) \\ \end{split}\]
Mentre per le backward probabilities (DEF), ho la seguente definizione
\[\beta_k(s) = P(o_k, \ldots, o_1 | x_k = s, \lambda)\]
e sono calcolate ricorsivamente nel seguente modo
\[\begin{split} \beta_{k}(q) &:= \sum\limits_{q \in S} a_{s, k} \cdot b_q(o_{k+1}) \cdot \beta_{k+1}(q) \\ \end{split}\]
A questo punto posso considere la probabilità di passare nel generico stato \(s \in S\) al \(k\) esimo ticktime nel seguente modo
\[\gamma_k(s) = P(X_k = s | Z, \lambda)\]
questa probabilitò può essere calcolata nel seguente modo
\[\gamma_k(s) = \frac{\alpha_k(s) \cdot \beta_k(s)}{P(X_k | Z, \lambda)} = \frac{\alpha_k(s) \cdot \beta_k(s)}{\sum_{q \in S} \alpha_k(q)}\]
A partire dai vari \(\gamma_k(s)\) posso poi calcolare il numero medio di transizioni che passano per lo stato \(s\)
\[\mathbb{E}[\text{# of transitions from } s] = \sum\limits_{k = 1}^{t-1} \gamma_k(s)\]
In modo analogo posso definire la probabilità di effettuare una particolare transizione al ticktime generico \(k\)
\[\xi_k(q, s) = P(X_k = q, X_{k+1} = s | Z, \lambda)\]
questa probabilità può essere calcolata come segue
\[\xi_k(q, s) = \eta_k \cdot \alpha_k(q) \cdot T_{q, s} \cdot E_{s, o_{k+1}} \cdot \beta_{k+1}(s)\]
dove \(\eta_k\) è un fattore di normalizzazione che viene utilizzato per garantire che
\[\sum\limits_{q, s \in S} \xi_k(q, s) = 1\]
Il numero medio di transizioni da \(q\) ad \(s\) è quindi calcolata come segue
\[\mathbb{E}[\text{# of transitioms from q to s}] = \sum\limits_{k = 1}^{t-1} \xi_k(q, s)\]
2.3 Updating Step
Una volta che ho calcolato i vari \(\gamma_k(s)\) e i vari \(\xi_k(s, q)\) posso aggiornare il modello \(\lambda = (E, T, \pi)\) per ottenere il nuovo modello \(\hat{\lambda} = (\hat{E}, \hat{T}, \hat{\pi})\) nel seguente modo:
Le nuove condizioni iniziali sono ottenute da dai vari \(\gamma_1(s)\), ovvero
\[\hat{\pi}_s = \gamma_1(s)\]
Le entry della nuova transition matrix sono ottenute nel seguente modo
\[\hat{T}_{q, s} = \frac{\mathbb{E}[\text{# of transitions from q to s}]}{\mathbb{E}[\text{# of transitions from q}]} = \frac{\sum_{k = 1}^{t-1} \xi_k(q, s)}{\sum_{k = 1}^{t-1} \gamma_k(q)} = \hat{P}(p \to s | q)\]
Le entryi della nuova emission matrix invece sono ottenute come segue
\[\begin{split} \hat{E}_{s, o} = \hat{b}_s(o) &= \frac{\mathbb{E}[\text{# of times in state s when the observation was o}]}{\mathbb{E}[\text{# of times in state s}]} \\ &= \frac{\sum_{k = 1}^t \gamma_k(s) \cdot \mathbb{1}(z_k = o)}{\sum_{k = 1}^t \gamma_k(s)} \\ &= \hat{P}(o|s) \\ \end{split}\]
2.4 Final Considerations
In generale quindi possiamo considerare il metodo di Baum-Welch come un esempio dell'algoritmo di Expectation-Maximization diviso in due step:
E-step (expectation step): In questo step si utilizza il modello precedente \(\lambda\) per calcolare le seguenti quantità
\[\begin{split} \sum\limits_{k = 1}^{t} \gamma_k(i) &= \text{expected numbers of transitions involving } q_i \\ \sum\limits_{k = 1}^{t-1} \xi_k(i, j) &= \text{expected numbers of transitions from } q_i \text{ to } q_j \\ \end{split}\]
M-step (likelihood maximization step): In questo step utilizzando le quantità calcolate prima per ottenere il nuovo modello
\[\begin{split} \hat{a}_{i, j} &= \frac{\sum_{k = 1}^{t-1} \xi_k(i, j)}{\sum_{k = 1}^{t-1} \gamma_k(j)} \;\;\;\; &\text{(transition matrix)}\\ \\ \hat{b}_i(o) &= \frac{\sum_{k = 1}^{t-1} \gamma_k(i) \cdot 1(z_k = o)}{\sum_{k = 1}^{t-1} \gamma_k(i)} \;\;\;\; &\text{(emission matrix)}\\ \end{split}\]
Attraverso lo studio della sequenza \(Z\) osservata, sto prendendo ciò che \(\lambda\) mi dà e lo spalmo su tutti gli articoli a disposizione, e poi sommo il sale in media che è andato a finire nelle singole frasi.
Fare la media significa redistribuire il sale, e il sale viene redistribuito in modo da premiare le cose che vengono spiegate da lambda meglio e più frequentemente. Non stiamo imettendo della nuova informazione, ma stiamo creando un decoding che è più in armonia con il modo in cui scrivono i giornalisti.
Il metodo di Baum-Welch è un esempio di schema di semi-supervised learning, in quanto utilizza una piccola porzione di dati etichettati e una grande porzione di dati non etichettati.
È possibile dimostrare (Baum et al., 1970) che il nuovo modello \(\hat{\lambda}\) è tale che \(P(Z|\hat{\lambda}) \geq P(Z | \lambda)\) e P(Z|\hat{\lambda}) = P(Z | )$ solamente se \(\lambda\) è un punto critico (massimo locale) per la funzione likelihood.
3 Example of HMM
Consideriamo la seguente HMM
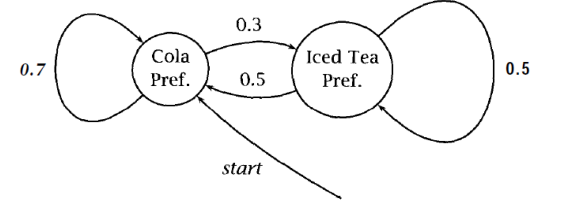
La matrice di output invece è la seguente
\[\begin{array}{c | c | c | c} \text{} & \text{cola} & \text{iced_tea} & \text{lemonade}\\ \hline \text{CP} & 0.6 & 0.1 & 0.3 \\ \text{IP} & 0.1 & 0.7 & 0.2 \\ \end{array}\]
Supponiamo poi di considerare una sequenza \(Z\) come la seguente sequenza di tre simboli
\[(\text{lem}, \text{ice_t}, \text{cola})\]
A questo punto posso calcolare le forward probabilities \(\gamma_k(\cdot)\) e le backwards probabilities \(\beta_k(\cdot)\).
TODO...
4 Use Cases for HMMs in NLP
Vediamo come si utilizzano questi modelli HMMs per affrontare varie problematiche nel contesto del natural language processing.
POS tagging: associare ad ogni parola la sua particolare classe.
Keyword spotting: Mettere a \(0\) le parole che voglio eliminare, e mettere a \(1\) quelle che voglio considerare.
Bracketing: Dire, per ogni parola, se essa appartiene all'inizio di una parentesi \((\), in mezzo a due parentesi, e alla fine di una parentesi \()\).
Il bracketing in particolare può poi essere utilizzato per:
named entity recognition:
multi word expressions
4.1 HMM Decoding for NLP
Il procedimento discusso in queste lezioni, ovvero la modellazione tramite HMM e la risoluzione del problema della codifica, può essere applicato a tanti task strutturati.
Per ciascuna applicazione, se vogliamo utilizzare un modello HMM, dobbiamo effettuare le seguenti scelte:
Come prima cosa dobbiamo prendere il task (tipicamente di NLP), e lo dobbiamo mattere in una sequenza di problemi di classificazione.
Dobbiamo definire una rappresentazione specifica per il problema che si vuole affrontare.
Una funzione di predizione \(F\).
Un algoritmo di apprendimennto utilizzato per approssimare \(f\) con l'ipotesi \(h\).
5 Exercise
