WMR 16 - PAC Learnability
Lecture Info
Date:
Course Site: Web Mining e Retrieval (a.a. 2019/20)
Lecturer: Roberto Basili.
Slides: ()
Table of Contents:
In questa lezione generalizziamo il concetto di apprendimento tramite il concetto di PAC learnability. La lezione di oggi è ripresa dal libro Introduction to Machine Learning.
1 On Learning
Fino adesso abbiamo descritto vari approcci algoritmici al machine learning, tra cui:
Alberi di decisioni.
Approcci probabilistici (Naive Bayes).
Approcci geometrici (Rocchio).
In tutti questi vari scenari abbiamo separatamente definito cosa significasse apprendere una funzione di decisione. Cercando di generalizzare il problema dell'apprendimento ci possiamo quindi porre la seguente domanda: cosa significa apprendere nel senso più generale possibile?
In generale imparare a risolvere un problema consiste nell'imparare a prendere una decisione. Nel particolare caso della classification la decisione consiste nel capire se una particolare istanza \(x\) fa parte di una particolare classe \(C\).
Per esempio conoscere il concetto di "family car" corrisponde a saper essere in grado di rispondere alla seguente domanda: "la macchina \(x\) è una family car?". Per fare questo l'idea è quella di estrarre dalle nostre osservazioni, tutte le informazioni che caratterizzano in particolare l'insieme delle "family car". Matematicamente questo consiste nell'apprendere la funzione caratteristica della classe di interesse.
La funzione che impara il concetto della classe prende in input l'insieme delle osservazioni, e ritorna in output la funzione imparata, che tipicamente ritorna 2 valori distinti: uno per l'appartenenza dell'istanza alla classe (valori positivi \(+\)), e l'altro per la non-appartenenza (valori negativi \(-\)).
1.1 Training Set
Il primo step per andare ad imparare questa funzione è quella di scegliere lo spazio delle rappresentazioni, ovvero il generico vettore che contiene gli attributi per ogni istanza osservata.
Nel caso dell'esempio della "family car", possiamo considerare almeno i seguenti due attributi: il prezzo \((x_1)\) e la potenza del motore \((x_2)\). Una volta definiti questi attributi abbiamo essenzialmente uno spazio geometrico in cui si trovano le varie istanze osservate.
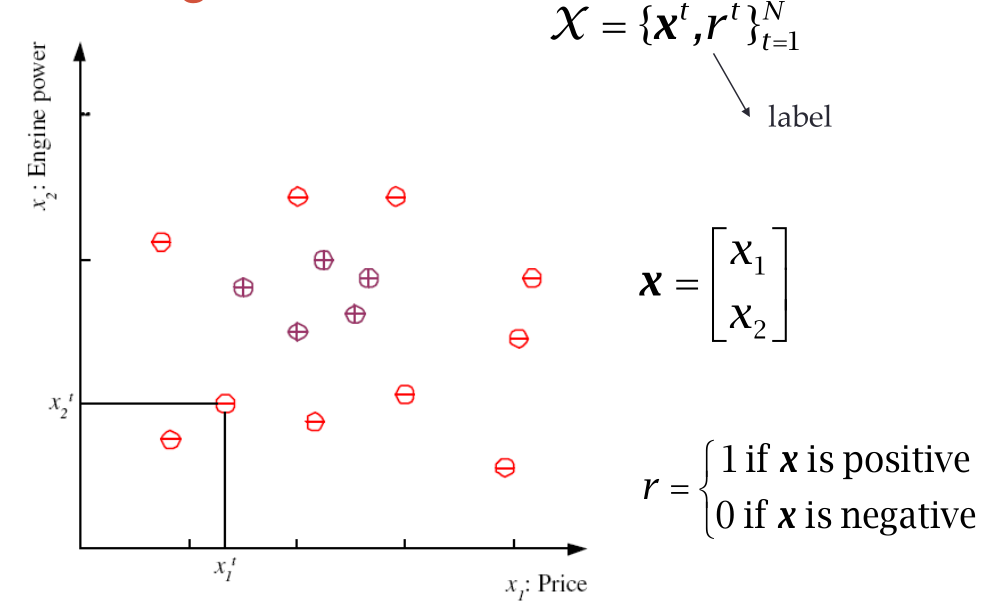
1.2 Learning Class \(C\)
Un primo approccio quindi per imparare la classe \(C\) di interesse potrebbe essere quello di esprimere dei vincoli sugli attributi. Ad esempio potremmo dire che tutte le istanze della classe \(C\) rispettano le seguenti condizioni
\[(p_1 \leq \text{ price } \leq p_2) \land (e_1 \leq \text{ engine power } \leq e_2)\]
Geometricamente questo definisce una regione dello spazio mostrato prima.
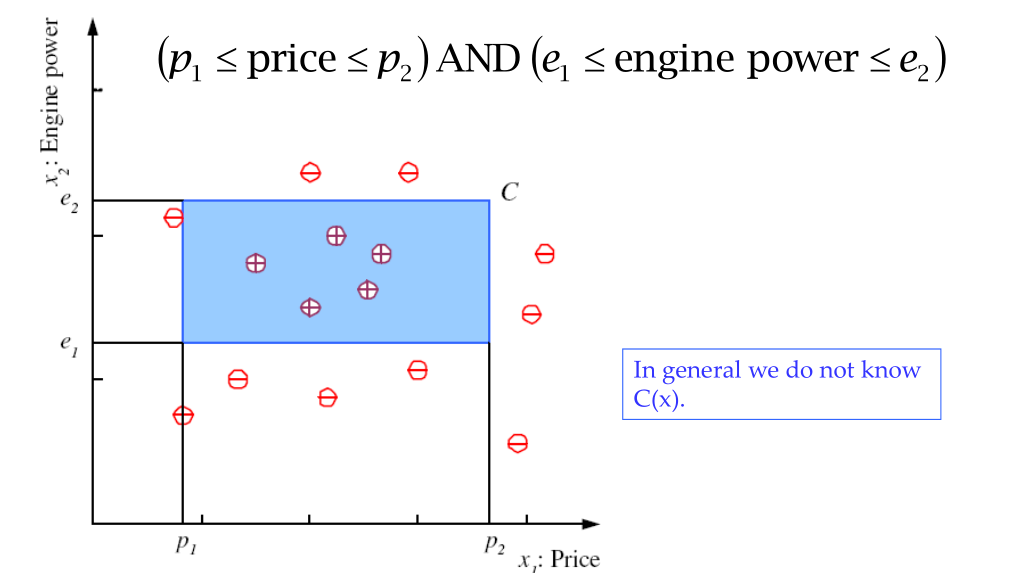
Noi però non conosciamo esattamente la legge \(C(x)\), però possiamo vedere che i punti che dobbiamo classificare possono essere effettivamente ben racchiusi all'interno di un rettangolo. Troviamo quindi una famiglia di funzioni al variare dei quattro parametri \((p_1, p_2, e_1, e_2)\).
Ad esempio possiamo quindi avere la seguente ipotesi
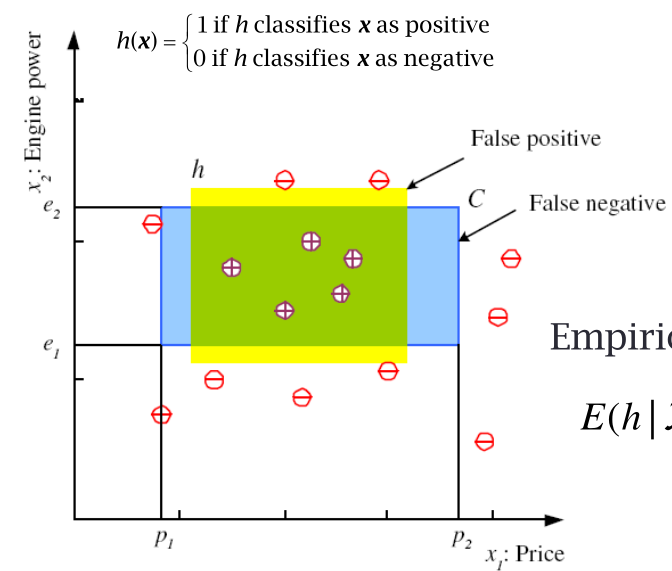
Ad ogni ipotesi possiamo poi associare l'errore empirico, che è la somma dei punti di training che vengono classificati male dall'ipotesi effettuata. In particolare, definita \(E(h|\mathcal{X})\) come la stima dell'ipotesi \(h\) rispetto al training set \(\mathcal{X}\), troviamo
\[E(h|\mathcal{X}) = \sum\limits_{t = 1}^N 1\Big(h(x^t) \neq r^t\Big)\]
dove,
\[1\Big(h(x^t) \neq r^t\Big) = \begin{cases} 1 & h(x^t) \neq r^t \\ 0 & h(x^t) = r^t \\ \end{cases}\]
Tramite questa funzione di errore possiamo quindi esplorare lo spazio delle ipotesi in modo guidato. In altre parole, apprendere significa esplorare lo spazio delle ipotesi in modo guidato.
1.3 Version Space
Lo spazio delle ipotesi "utilizzabili" è anche detto spazio delle versioni, o version space, ed è costituito dalle ipotesi \(h \in \mathcal{H}\) contenute tra l'ipotesi più specifica \(S\) e l'ipotesi più generale \(G\).
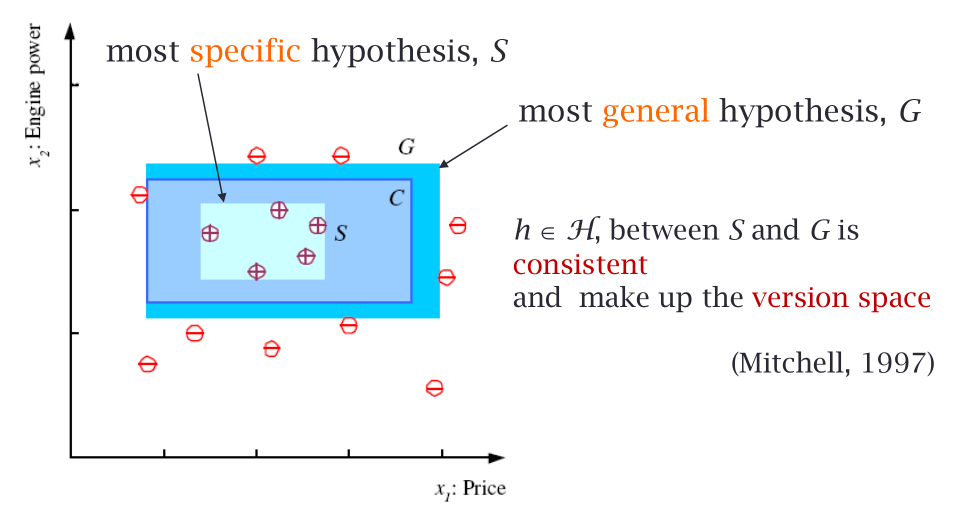
Notiamo che sia l'ipotesi più specifica \(S\) che quella più generale \(G\) dividono i positivi dai negativi, ma mentre la prima lo fa stando il più vicino possibile ai positivi, la seconda lo fa stando il più vicino possibile ai negativi. Dei falsi negativi producono delle espansioni di \(S\), mentre dei falsi positivi producono delle contrazioni di \(G\).
Osservazione: Il rettangolo \(C\) è il concetto che vogliamo apprendere. Certe volte però \(C\) non esiste. In questi casi non ha senso calcolare né \(S\) né \(G\). Molto spesso oggi però la gente cerca di imparare dai dati dei concetti che non esistono.
Se \(C\) non esiste siamo tutti fottuti.
Per fare questo ragionamento abbiamo quindi bisogno delle seguenti cose:
Di sapere come è fatta la rappresentazione dei nostri dati. Nel caso del nostro esempio questo è rappresentato dallo spazio \(\mathbb{R}^2\) formato dalle coppie di valori reali \((\text{price}, \text{engine power})\).
Il concetto \(C\) nello spazio di rappresentazione esiste.
2 PAC Learning
PAC per Probably Approximately Correct.
Possiamo quindi immaginare il processo di learnability come un processo che fa due cose:
Dopo aver fissato una famiglia di funzioni, scelgo da questa famiglia una funzione che ha una probabilità di compiere degli errori molto bassa;
Approssimo la funzione menzionata prima tramite un processo su cui ho molta confidenza, ovvero durante il processo di selezione ho minimizzato la probabilità di aver sbagliato ad individuare la corretta funzione.
Notiamo quindi che abbiamo due fonti di aleatorietà: la prima deriva dal fatto che ho una infinità di scelta per quanto riguarda la funzione utilizzata per apprendere i dati, e successivamente ciascuna funzione si può comportare più o meno bene rispetto ai dati del futuro.
In generale vogliamo essere confidenti di scegliere al meglio le funzioni che fanno pochi errori. Per quanto riguarda la confidenza, questa è regolata da un valore \(\delta\). In particolare per piccoli valori di \(\delta\) avrò grandi valori di confidenza. Detto altrimenti, la confidenza è data da \(1 - \delta\). Per quanto riguarda la probabilità di errore della funzione scelta invece, questo è regolato da un valore \(\epsilon\).
2.1 PAC-Learnability
Una classe di concetti \(C\) è detta PAC-learnable se esiste un PAC-learning algorithm tale che, per ogni \(\epsilon > 0\) e per ogni \(\delta > 0\), esiste un size fissato, tale che, per ogni concetto \(c \in C\) e per ogni distribuzione sul training set \(\mathcal{X}\) rispetto al concetto \(c\), l'algoritmo di learning utilizzando al più size fissato osservazioni della distribuzione \(\mathcal{X}\), produce una ipotesi \(h\) detta probably-approximately-correct, ovvero tale che l'ipotesi \(h\) generata ha un errore al più di \(\epsilon\) con probabilità almeno \(1 - \delta\).
Nel PAC learning (Blumer, et al. 1989), data una classe \(C\) e degli esempi estratti da una ignota ma fissata distribuzione \(p(x)\), vogliamo capire qual è il numero di esempi \(N\) tale che con probabilità almeno \(1 - \delta\) l'ipotesi \(h\) ottenuta compie un errore di al più \(\epsilon\). In formula
\[P(C\Delta h \leq \epsilon) \geq 1 - \delta\]
dove \(C\Delta h\) è l'area della regione ottenuta dalla differenza tra \(C\) e \(h\), con \(\delta > 0, \epsilon > 0\).
Una classe di concetti \(C\) è detta PAC-learnable se esiste un PAC-learning algorithm tale che, per ogni \(\epsilon > 0\) e per ogni \(\delta > 0\), esiste un campione di size fissato, tale che, per ogni concetto \(c \in C\) e per ogni distribuzione sul training set \(\mathcal{X}\) rispetto al concetto \(c\), l'algoritmo di learning produce una ipotesi \(h\) detta probably-approximately-correct, ovvero tale che l'ipotesi \(h\) generata ha un errore al più di \(\epsilon\) con probabilità almeno \(1 - \delta\).
Nel PAC learning (Blumer, et al. 1989), data una classe \(C\) e degli esempi estratti da una ignota ma fissata distribuzione \(p(x)\), vogliamo capire qual è il numero di esempi \(N\) tale che con probabilità almeno \(1 - \delta\) l'ipotesi \(h\) ottenuta compie un errore di al più \(\epsilon\). In formula
\[P(C\Delta h \leq \epsilon) \geq 1 - \delta\]
dove \(C\Delta h\) è l'area della regione ottenuta dalla differenza tra \(C\) e \(h\), con \(\delta > 0, \epsilon > 0\).
2.2 Example
Proviamo quindi a rispondere alla domanda: how many training examples \(m\) should we have, such that with probability at least \(1 - \delta\), \(h\) has error at most \(\epsilon\)? rispetto al nosto esempio di prima in cui \(C\) è modellato come un rettangolo.
Alla fine troviamo
\[m \geq \frac{4}{\epsilon} \cdot \ln{\Big(\frac{4}{\delta}\Big)}\]
quindi, ad esempio
Se \(\epsilon = 1\%\) e \(\delta = 5\%\), allora \(m \geq 1752\)
Se \(\epsilon = 10\%\) e \(\delta = 5\%\), allora \(m \geq 175\)
3 VC-Dimension
Nell'esempio visto prima la classe \(C\) poteva essere descritta bene da un semplice rettangolo. Questo in generale non è sempre il caso, e quando \(C\) non è un semplice rettangolo, ma ha una forma più complessa, la complessità della funzione \(h\) cresce di conseguenza.
Nel caso di funzioni più complesse si cerca di discretizzare la capacità che una funzione ha di separare i dati che appartengono ad un concetto \(C\) e i dati che non appartengono al concetto \(C\). A tale fine si introduce il concetto di VC-Dimension (VC per Vapnik-Chervonenkis)-.
Consideriamo il fatto che \(N\) punti possono essere classificati in \(2^N\) modi diversi, dove ciascun modo dice se ciascun punto fa o meno parte di una fissata classe \(C\).
Data una famiglia di funzioni \(\mathcal{H}\), diciamo che \(\mathcal{H}\) shatters \(N\), se esiste un insieme di \(N\) punti tali che \(h \in \mathcal{H}\) è consistente con tutti le possibili classificazioni di questi punti. Questo valore \(N\) è detta la VC Dimension della famiglia \(\mathcal{H}\), e viene utilizzato per misurare la capacità di separare i punti della famiglia \(\mathcal{H}\).
Questo significa che se ho \(N\) esempi, allora ho bisogno almeno di una classe di funzioni che sia in grado di separarli.
3.1 Axies Aligned Rectangles
La VC-Dimension della classe di funzioni che rappresentano rettangoli nel piano è \(4\), in quanto tramite dei rettangoli siamo in grado di classificare in modo consistente tutti i punti in ciascuna delle \(2^4\) possibili classificazioni diverse.
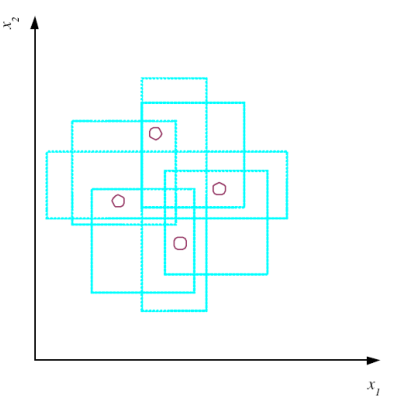
Se invece abbiamo \(N=5\) punti, questo non è più possibile.
Notiamo che nella definizione di VC-Dimension la scelta dei punti è arbitraria, nel senso che possiamo noi sceglire \(N\) particolari punti. Dobbiamo però testare che il modello è consistente rispetto a tutte le possibili classificazioni dei vari punti.
La VC-Dimension ci offre una visione molto pessimistica del comportamento della classe di funzioni da noi scelta. Può quindi essere utilizzati come uno strumenti per iniziare a capire se la classe scelta è giusta. Detto questo, il suo limite è proprio la sua generalità, in quanto non tutte le possibili classificazioni sono sempre di interesse.
3.2 Lines
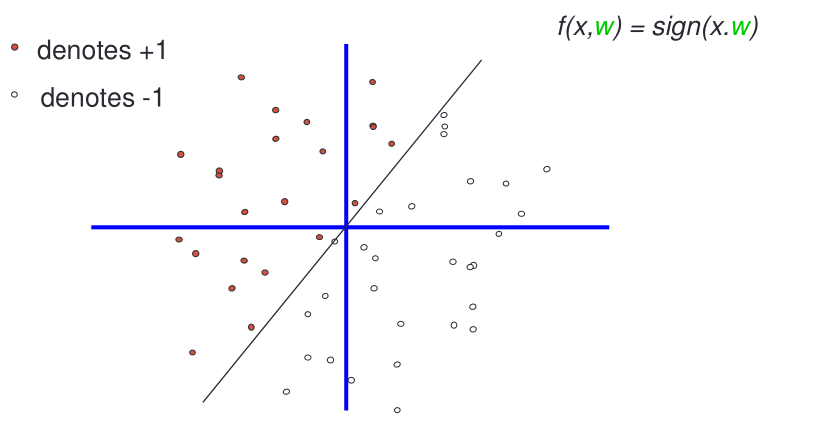
Consideriamo la famiglia delle rette che passano per l'origine e che dipende dai parametri \(\alpha\). In particolare questa classe ha un parametro \(\w\), che descrive il coefficiente angolare della retta, mentre il termine noto è fissato a \(0\).
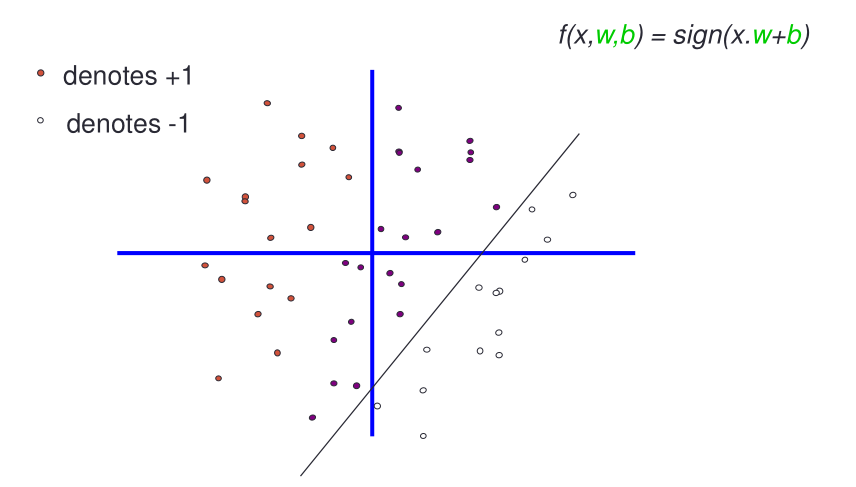
Una famiglia un pochino più espressiva è invecela famiglia delle rette che hanno un termine noto arbitrario. Quest'altra famiglia ha due parametri: \(w\) e \(b\).
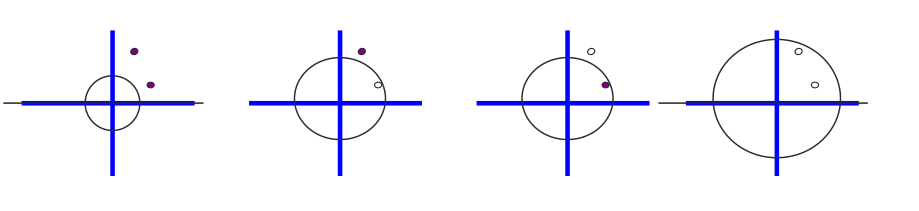
Per calcolare la VC-dimension delle rette passanti per l'origine poniamoci la seguente domanda: siamo in grado di spezzare i seguenti punti?

La risposta è positiva, in quanto tramite delle rette passanti per l'origine siamo in grado di dividere questi punti rispetto a tutte le possibili classificazioni.
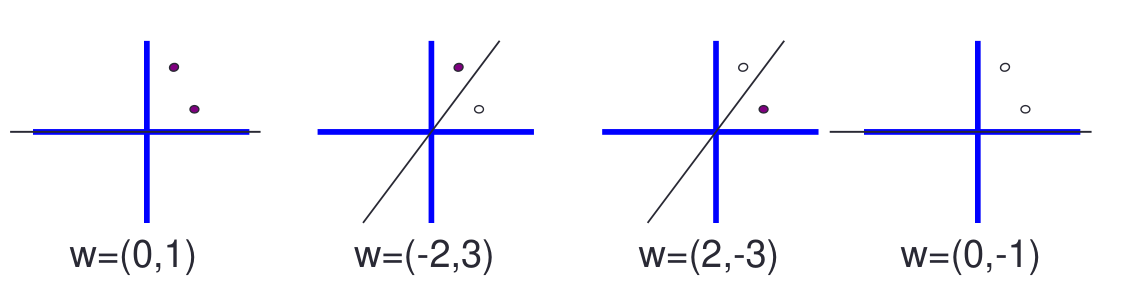
Possiamo quindi concludere che la VC-dimension delle rette passanti per l'origine è almeno \(2\).
In generale dato uno spazio di input \(m\) dimensionale, se \(f\) è la funzione \(\text{sign}(w, x - b)\), dove \(w\) e \(b\) sono i parametri del modello, abbiamo che la VC-dimension di tale famiglia di funzioni è \(h=m+1\), in quanto
Punti \(1d\) possono separare \(2\) punti.
Line \(2D\) possono separare \(3\) punti.
Piani \(3D\) possono separare \(4\) punti.
...
All'aumentare della dimensionalità aumentano il numero di parametri del nostro modello lineare, e di conseguenza il numero di punti che posso separare.
In generale la VC-dimension mi dice qual è il potere di approssimare delle fenomenologie che avvengono nello spazio da parte di una classe di funzioni.
3.3 Circles
Consideriamo adesso la funzione dei cerchi con un dato raggio e centrati nell'origine
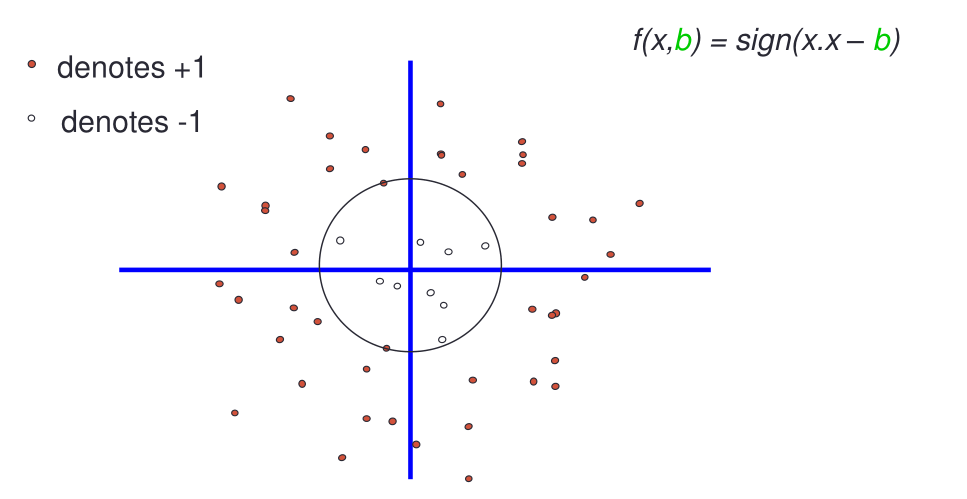
Notiamo che la VC-dimension di questa classe di funzioni è almeno \(3\)