WMR 17 - Model Selection

Lecture Info

Date: [2020-04-20 lun]
Course Site: Web Mining e Retrieval (a.a. 2019/20)
Lecturer: Roberto Basili.
Slides: ()
Table of Contents:

In questa lezione abbiamo parlato della model selection utilizzando la VC-dimensionality come misura di complessità tramite la structural risk minimization.

1 Model Selection

Nell'apprendimento vogliamo scegliere la \(h \in \mathcal{H}\) in modo da rappresentare una buona generalizzazione dei dati di training.

Il numero di osservazioni che necessitiamo per apprendere concetti complessi però è molto grande, e in generale non avrò mai abbastanza training data per gestire tutti i casi possibili. L'idea è quindi di utilizzare i pochi dati di training per ottenere il modello migliore.

Modelli diversi hanno un potere di generalizzazione diverso. In particolare più grande è la VC-dimension di una famiglia di funzioni, e maggiore sarà il potere dei modelli estratti da quella famiglia (viceversa per il caso contrario).

In generale abbiamo due fenomeni diversi, ugualmente pericolosi, in cui possiamo cadere quando effettuiamo dell'apprendimento:

Overfitting: \(\mathcal{H}\) more complex than \(C\) or \(f\).
Underfitting: \(\mathcal{H}\) less complex than \(C\) or \(f\).

1.1 Triple Trade-Off

Il trade-off dei vari modi è calcolato in base ai seguenti tre fattori:

La complessità della famiglia \(\mathcal{H}\), ovvero la VC-dimensione di \(\mathcal{H}\).
Il size del training set \(N\).
L'errore di generalizzazioen \(E\) sui nuovi dati.

In generale abbiamo che:

All'aumentare il numero di esempi \(N\), l'errore tende a divenire sempre più piccolo.
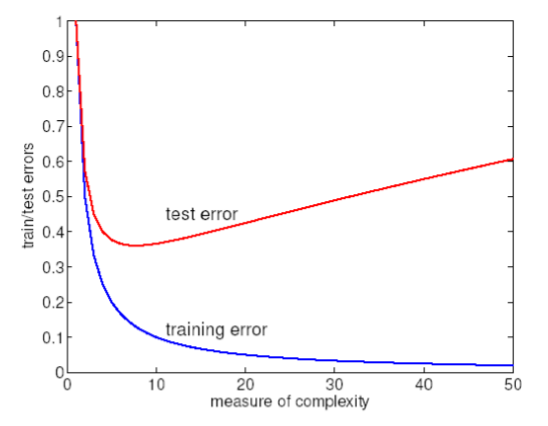
Più la VC-dimension è alta, e più l'errore empirico tende prima a diminuire di molto (nei dati di training), e poi ad aumentare (nei dati di testing).

In generale abbiamo bisogno di una misura della complessità dei nostri modelli di apprendimento in modo da relazionare il training error (che possiamo calcolare) al test error (che vogliamo ottimizzare)

1.2 Expected and Empirical Error

Ricordiamo che per misurare l'errore sul training set possiamo utilizzare l'errore empirico, definito come segue

\[\hat{\epsilon}_n(i) = \frac{1}{n} \sum\limits_{t = 1}^n \text{Loss}(y_t, h_i(x_t))\]

dove \(\text{Loss}(y_t, h_i(x_t))\) è definita come segue

\[\text{Loss}(y_t, h_i(x_t)) = \begin{cases} 1 &, y_t \neq h_i(x_t) \\ 0 &, y_t = h_i(x_t) \\ \end{cases}\]

Quello che a noi interessa però è il test error, ovvero l'errore sui dati reali con cui il modello dovrà lavorare. Dato che non possiamo calcolare direttamente questo valore, lo possiamo stimare tramite l'errore atteso

\[\epsilon(i) = \mathbb{E}_{(x, y)} \; \{\text{Loss}(y, h_i(x))\}\]

1.3 Learning and VC-Dimension

Per misurare la complessità ci sono varie possibili strade, tra cui:

Degrees of freedom.
Description length.
Vapnik-Chervonenkis (VC) dimension.
...

Ci sono persone che si sono messe a studiare la relazione tra l'errore empirico, che è calcolabile, e quello sui dati del futuro, che possiamo solo stimare, andando a capire lo scarso in funzione dei parametri \(n, d_{\text{VC}}, \delta\), dove

\(n\) è il numero di osservazioni del training set.
\(d_{\text{VC}}\) è la VC dimension del modello scelto.
\(1 - \delta\) è la probabilità che la funzione sia perfetta nello scegliere la classificazione per ogni classe.

Troviamo quindi il seguente teorema.

Theorem: With probability at least \(1 - \delta\) over the choice of the training set, for all \(h \in F\)

\[\xi(h) \leq \hat{\xi}_n(h) + \epsilon(n, d_{\text{VC}}, \delta)\]

dove,

\[\epsilon(n, d_{\text{VC}}, \delta) = \sqrt{\frac{d_{\text{VC}}(\log{(2n/d_{\text{VC}})} + 1) + \log{(1/(4\delta))}}{n}}\]

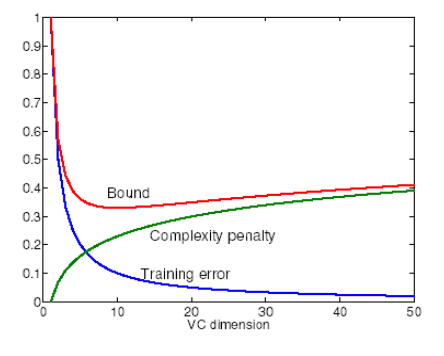
L'idea è quindi che al crescere della VC-dimension abbiamo una complexity penalty che viene aggiunto all'errore empirico per formare l'errore atteso.

1.4 How to Select a Model

Un possibile modo per selezionare un modello è quindi quello di trovare il modello che raggiunge il miglior equilibrio tra la complessità e l'abilità di spiegare i dati di training.

Posisamo quindi partire da una sequenza di modelli la cui complessità (VC-dimension) cresce

Model 1, \(d_1\)
Model 2, \(d_2\)
Model 3, \(d_3\)
...

con \(d_1 \leq d_2 \leq d_3 \leq \ldots\).

E per selezionare il modello tra questa sequenza considero il modello che riesce ad ottenere il più piccolo upper bound nell'errore atteso, dove

\[\text{ Expected error} \leq \text{Training error } + \text{ Complexity penalty }\]

1.4.1 Example (Structural Risk Minimization)

Consideriamo un esempio con \(n = 50\) istanze di training e un confidence parameter di \(\delta = 0.05\). Andando ad analizzare in successione una serie di modelli polinomiali di complessità crescente

\[\begin{array}{c | c | c} \textbf{Model} & d_{\text{VC}} & \textbf{Empirical fit} & \epsilon(n, d_{\text{VC}, \delta}) \\ \hline 1 & 3 & 0.06 & 0.5501 \\ 2 & 6 & 0.06 & 0.6999 \\ 4 & 15 & 0.04 & 0.9494 \\ 8 & 45& 0.02 & 1.2849 \\ \end{array}\]

Graficamente vediamo la seguente situazione

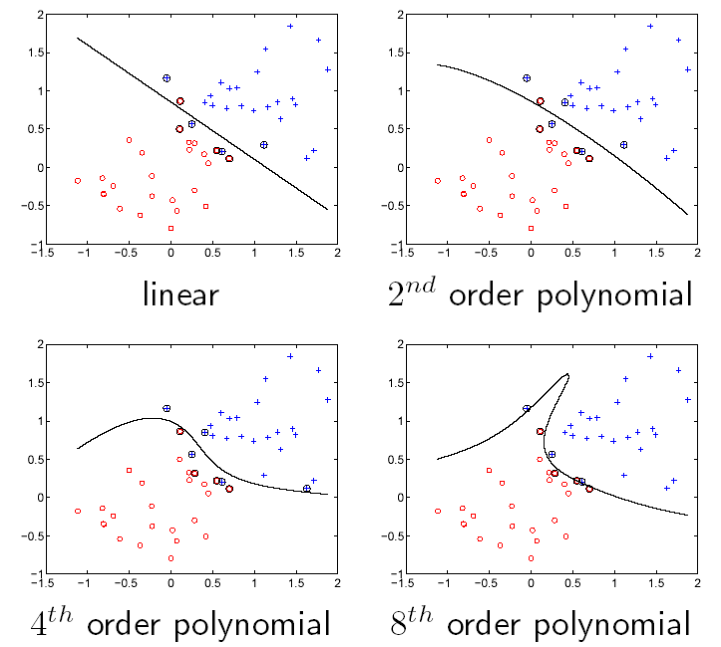
Se scegliamo un modello andando a minimizzare il fattore di rischio nel futuro, abbiamo uno schema di structural risk minimization. Nel caso dell'esempio precedente il modello scelto sarebbe quindi il primo, ovvero quello lineare.

2 Learning Machines

Una learning machine è una famiglia di funzioni \(f\) parametrizzata in \(\underline{\alpha}\) (i cui elementi sono detti anche fattori, pesi o parametri), che prende un input \(x\) e lo trasforma in un output predetto \(y^{\text{est}} = \pm 1\), che è la stima della categoria di uscita.

Data una learning machine \(f\), definiamo

Test error, la probabilità di missclassification nelle istanze future

\[R(\alpha) = \text{TESTERR}(\alpha) = \mathbb{E}\Big[ \frac12 | y - f(x, \alpha) | \Big]\]
Train error, la frazione del training set missclassificata

\[R^{\text{emp}}(\alpha) = \text{TRAINERR}(\alpha) = \frac{1}{R} \sum\limits_{k = 1}^R \frac12 | y_k - f(x_k, \alpha)|\]

dove \(R\) è il numero di data points del training set.

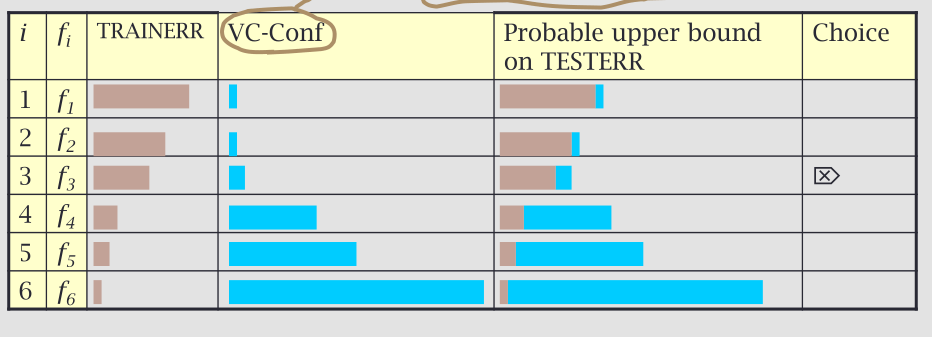
Consideriamo poi la VC-dimesione \(h\) della learning machine \(f\). Allora abbiamo che con p robabilità \(1 - \delta\) vale

\[\text{TESTERR}(\alpha) \leq \text{TRAINERR}(\alpha) + \sqrt{\frac{h(\log{(2R/h)} + 1) -\log{(\delta/4)}}{R}}\]

In altre parole, siamo in grado di stimare l'errore sui dati del futuro a partire dal training error e della VC-dimension di \(f\).

3 Using VC-Dimensionality

La VC-dimension è stata studiata per varie macchine di apprendimento, tra cui:

Decision trees.
Perceptrons.
Neural Nets.
Decision Lists.
Support Vector Machines.
...

Questo è stato fatto per vari obiettivi, tra cui capire il potere delle varie macchine di apprendimento e anche utilizzare la strategia della structural risk minimization per scegliere la macchina di apprendimento migliore.

Anche se teoricamente la VC-dimensionality può essere utilizzata per dare dei bound teorici al futuro errore del modello, nel corso degli anni sono state sviluppate strade alternative.

Un esempio di una strategia per fare model selection alternativa al basarsi sulla VC-dimensionality è la cross-validation, che ci permette di dare una stima all'errore di generalizzazione andando a splittare i dati di input in tre modi:

Training set \((50 \%)\).
Validation set \((25 \%)\).
Test (pubblication) set \((25 \%)\).

References. C.J.C. Burges. A tutorial on support vector machines for pattern recognition. Data mining and Knowledge Discovery.

4 Recap

Un recap generale delle nozioni trattate nelle ultime due lezioni (compresa questa):

Apprendere significa muoversi attraverso spazi di funzioni cercando di soddisfare due criteri:

Aumentare la confidenza con cui si sceglono funzioni quando si apprendere. (probabilità di avere una \(h\) che non sbaglia mai)
Far si che l'errore del modello tende a diventare sempre più piccolo all'aumentare dei dati di training.

Questi due concetti, presi assieme, ci dicono che le funzioni adeguate sono quelle che hanno un'alta probabilità di essere corretta nella migliore approssimazione possibile.

Nel PAC learning questa aleatorietà viene modellata come la ricerca di una funzione tra una sequenza di funzioni, e una macchina di apprendimento è una macchina che definita una famiglia di funzioni, elabora il vettore dei parametri in modo da scegliere la funzione specifica appartenente alla famiglia fissata.

La VC-dimension è una misura che ci permette di capire la capacità di una funzione di rompere (shatter) i dati di input su cui fare training.

Utilizzando la VC-dimension come misura di complessità siamo in grado di utilizare la structural risk minmization come strategia per fare model selection.

Nella pratica però non viene utilizzata la structural risk minimization esattamente come è stata esposta a livello teorico, ma vengono utilizzati approcci più empirici che simulano questo tipo di ricerca. Uno di questi approcci è la cross-validation, che è un modo empirico per seguire la teoria del PAC-learning, utilizzando però non i bound teorici ma i dati osservabili.